解析几何之“三定”问题解题策略的探究

李俊丽

(山西师范大学实验中学,山西 临汾 041000)

圆锥曲线一直是考查解析几何知识的重要载体,纵观近几年的高考试题,圆锥曲线的大题较多考查直线与圆锥曲线的位置关系问题,题目的设计常常紧扣解析几何研究的两条主线:一是根据条件利用待定系数法先行确定曲线的标准方程;二是以不同曲线与直线的位置关系为基础设计题目,结合曲线的定义及几何性质进一步研究直线方程、斜率、弦长、图形面积等,比如“中点弦”问题、定点、定值、定直线问题、范围与最值问题、探索性问题等.

1 题型与方法探究

1.1 点在定直线上的问题

(1) 求C的方程;

(2) 记C的左、右顶点分别为A1,A2, 过点 (-4,0) 的直线与C的左支交于M,N两点,M在第二象限, 直线MA1与NA2交于点P.证明: 点P在定直线上.

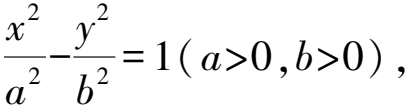
所以b2=c2-a2=16.

(2)方法1 (通性通法)由题意可知直线MN不与y轴垂直,设直线MN的方程为x=my-4,M(x1,y1),N(x2,y2),

(4m2-1)y2-32my+48=0.

其判别式Δ=32(8m2+6)>0,

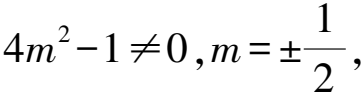
由A1(-2,0),A2(2,0),得

两式联立消去y,得

由M,N,(-4,0)三点共线得

化简,得(t1-t2)(t1t2+3)=0,t1≠t2.

所以t1t2=-3.

所以kMA1=-3kNA2.

1.2 直线过定点的问题

(1)求E的方程;

成品：发酵液体饲料需要保证的有益指标包括pH值、乳酸、乳酸菌，需要控制的有害指标包括乙酸、尸胺、大肠杆菌、沙门氏菌。刘金萍等[14]研究表明，为了减少或者限制饲料中的沙门氏菌，有必要维持乳酸浓度为300 mol/l，维持适当的pH值（pH值≤4.5）。覃春富等[15]研究指出，通过气味和观察色泽可以判断液体饲料各阶段的发酵效果（见表4）。

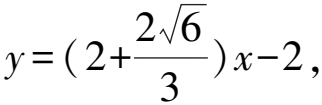
②当直线MN与x轴不垂直时,设直线MN方程为y+2=k(x-1),设M(x1,y1),N(x2,y2),

(3k2+4)x2-6(k2+2k)x+3k2+12k=0.

其判别式Δ>0,

所以直线HN方程为

将点(0,-2)代入化简得6(y1+y2)+3y1·y2-2(x1+x2)-(x1·y2+x2·y1)+12=0.

①

综上可得直线HN过定点(0,-2).

1.3 定值问题

(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,点D为垂足．证明:存在定点Q,使得|DQ|为定值．

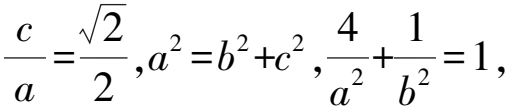
x2+4x+2y2+4y=0.

设直线MN的方程为mx+ny=4,

x2+x(mx+ny)+2y2+y(mx+ny)=0.

即(1+m)x2+(2+n)y2+(m+n)xy=0.

代入直线MN方程中得n(y-x)-3x-4=0.

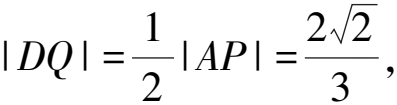
2 总结反思

2.1 对解析几何“三定”问题解法的思考

解析几何解答题中的“三定”问题,是一类高考常考题型,这类题目的核心解题方法是“坐标法”.解题过程一般是设出直线方程和点的坐标,联立消元合理变形,利用根与系数的关系整体代换求解.另外,还可以利用平移坐标系法、巧设曲线系方程或参数方程求解,方法灵活,综合性强.这充分体现了数形结合、方程、整体代换的思想,主要考查学生的转化与化归、推理论证、运算求解能力.

2.2 对解析几何问题教学的思考

2.2.1重视基础,深化核心知识教学

解析几何问题思维量和运算量大,在复习过程中应坚持把教学重心放在对关键能力提升、学科素养发展具有支撑作用的基础知识、基本技能与基本思想方法上,要引导学生在深刻理解基本概念和性质的基础上,弄清知识的来龙去脉,把握知识的内在联系,构建整体知识体系.

2.2.2注重数学思想方法的渗透和能力的培养

解析几何问题的综合性很强,在复习的过程中要注重数形结合、整体代换、转化与化归等思想方法的训练,培养学生分析问题、解决问题的能力,提升其数学抽象、数学运算、逻辑推理和直观想象方面的学科核心素养.