深度探究一道抛物线模拟题
李 寒
(贵阳市第一中学,贵州 贵阳 550081)
数学的精髓在于不断探索和创新.在数学解题教学的实施过程中,应不断地从中发现新问题,获取有用的新信息,提出新颖观点,探求解决问题的新方法,归纳得出新规律,进而适时地将问题延伸推广为一般性结论用于解决相关联的问题.唯有这样,才能逐步培养学生灵活多变的思维品质和探索精神,提升学生的数学核心素养和创新意识,从而真正把能力的培养落到实处.
1 试题呈现
题目(2023届广州市一模第6题)已知抛物线C的顶点为坐标原点O,焦点F在x轴上,过点(2,0)的直线交C于P,Q两点,且OP⊥OQ,线段PQ的中点为M,则直线MF的斜率的最大值为( ).
2 试题解答
分析1 根据题设条件,设出抛物线C与直线PQ的方程,然后利用垂直关系求出抛物线C的方程及点M的坐标,再利用斜率公式建立函数关系,最后应用均值不等式解得最值.
解法1 由题可知,抛物线C的焦点F在x轴的正半轴上,设抛物线C的方程为y2=2px(p>0).

y2-2pty-4p=0.

y1y2=-4p.
由OP⊥OQ,得
解得p=1.

所以点M(t2+2,t).
显然若直线MF的斜率最大,则必有t>0.


故选A.
分析2 根据单选题的题型特点,利用下面抛物线的“二级结论1”,可迅速秒求p的值.
解法2见结论1证明之后.
3 结论推广
思考1过抛物线作两条互相垂直的弦,分别交抛物线于P,Q两点,则直线PQ具有怎样的位置关系?经探究,有:
结论1 过抛物线C:y2=2px(p>0)的顶点作两条互相垂直的弦,分别交抛物线于P,Q两点,则直线PQ必过定点(2p,0).

化简整理,得
2px-(y1+y2)y+y1y2=0.
由OP⊥OQ,得
解得y1y2=-4p2.
所以直线PQ的方程为
2px-(y1+y2)y-4p2=0.
令y=0,得x=2p.
所以直线PQ过定点(2p,0).
若直线PQ的斜率不存在,易得P(2p,2p),Q(2p,-2p),所以直线PQ仍过定点(2p,0).从而结论1得证.
根据结论1,我们可以给出试题的解法2了.
解法2由结论1可知2p=2,解得p=1.以下同解法1.
4 逆向探究
思考2 若对结论1进行逆向思考,即将直线过定点作为题设,是否能得到“垂直”关系?经探究,于是有:
结论2 过定点(2p,0)的直线分别交抛物线C:y2=2px(p>0)于P,Q两点,O为坐标原点,则OP⊥OQ.




故OP⊥OQ.
5 纵向探究
思考3 结论1中,OP⊥OQ中的点O是抛物线C上的一个特殊的定点(顶点),若把定点O换作抛物线C的其它位置,那么是否能够得到与结论1同样的结论?即直线PQ仍过定点呢?
结论3 过抛物线C:y2=2px(p>0)上的定点T(x0,y0)作两条互相垂直的弦,分别交抛物线于P,Q两点,则直线PQ必过定点(x0+2p,-y0).

化简整理,得2px-(y1+y2)y+y1y2=0.
①


因为点T(x0,y0)在抛物线C上,


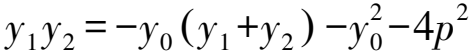
=-y0(y1+y2)-2px0-4p2.
代入①并整理,得
2p(x-x0-2p)-(y1+y2)(y+y0)=0.
可知直线PQ过定点(x0+2p,-y0).
若直线PQ的斜率不存在,即y2=-y1.
则直线PQ的方程为x=2p+x0.
此时显然直线PQ也过定点(x0+2p,-y0).
思考4 对于结论3中,若延长TP和TQ,则“TP⊥TQ”也可以理解为直线TP与直线TQ的倾斜角之差为90°,那么当直线TP与直线TQ的倾斜角之和为90°时,直线PQ是否也过定点呢?
结论4 过抛物线C:y2=2px(p>0)上的定点T(x0,y0)作倾斜角之和为90°的两条直线,分别交抛物线C于P,Q两点,则直线PQ必过定点(x0-2p,-y0).
结论4的证明,可仿照结论3的证明过程进行,这里从略,请读者自行完成.
思考5 沿着结论4的思路,进一步变换角度思考:当直线TP与直线TQ的倾斜角之和为180°时,直线PQ是否还过定点呢?有没有其它情形呢?
结论5 已知T(x0,y0)是抛物线C:y2=2px(p>0)上的一个定点,P,Q是抛物线C上使直线TP与直线TQ的倾斜角之和为180°的两点,则直线PQ的斜率为定值,即线段PQ是一组平行弦.
证明由题意可知直线TP与直线TQ均不垂直于坐标轴,即直线TP的斜率kTP与直线TQ的斜率kTQ均存在且不为0.
因为直线TP与直线TQ的倾斜角之和为180°,所以kTP+kTQ=0,即kTP=-kTQ.

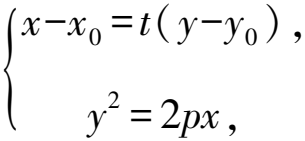
y2-2pty-2pty0-2px0=0.

所以y=y0(舍去)或y=2pt-y0.



因此直线PQ的斜率

故线段PQ是一组平行弦.
思考6 在结论5的基础上,作一般性思考:当直线TP与直线TQ的斜率之积为常数时,直线PQ是否也能够过定点呢?


化简整理,得
2px-(y1+y2)y+y1y2=0.
①
由kTP·kTQ=λ,得

因为点T(x0,y0)在抛物线C上,




代入①并整理,得

6 类比探究
思考7 椭圆、双曲线与抛物线有许多类似的结论,能否将抛物线的结论3类比推广到椭圆和双曲线呢?经探究,于是有:


结论7与结论8的证明可按结论3的证明过程进行,这里从略,请读者自行完成.
对典型模拟题的多角度探究,就是指对问题从不同视角来审视,以不同的切入点探究问题,其实质是对试题的“二次开发”.通过对试题的剖析和思考,展开问题的来龙去脉和知识间的纵横联系,站在一定的高度去思考问题,突出数学本质,使知识达到融会贯通,使思维得到升华,进而优化数学思维品质[1].

