(3+1)维BLMP方程和(3+1)维非线性发展方程的lump解

张 琪

(1.山西省交城县城南小学，山西 吕梁 030500;2.山西应用科技学院 基础教学部，山西 太原 030062)

非线性偏微分方程解析解的构造是非线性科学中的一个热点问题.为了获得更多的精确解,近年来,数学家和物理学家研究出了各种不同的方法,如tanh函数方法[1]、双曲正割函数方法[2]、反散射变换方法[3]、Backlund变换[4]、齐次平衡方法[5]、广田双线性方法[6]、Darboux变换[7]、Wronskian方法[8]和指数函数方法[9]等等.除了精确解的构造方法以外,有效的近似解法包含Adomian分解法[10]、摄动法和同伦分析法[11]等.但是以上这些求解非线性偏微分方程的方法,在求解的过程还是具有一定的局限性,有时只能对某一类或具有某一种形式的方程才可能显式地表达出方程的解.所以,许多具有实际物理意义的新解现在还尚未被发现,因而需要我们利用更好的、更完善的方法来进一步地研究和构造.孤子解和lump解是孤子理论中最基本的解,而lump解则是一类有理函数解,指的是在空间上所有方向都趋于零的解[12],在对非线性现象的研究中占有十分重要的地位.因此,近年来lump解已经引起了人们极大的研究兴趣.

本文讨论(3+1)维Boiti-Leon-Manna-Pempinelli方程(以下简称BLMP方程)

uyz+uzt+uxxxy-3uxuxy-3uxuxz-3uxxuy-3uxxuz=0，

(1)

和一个(3+1)维非线性发展方程(以下简称NLEE)

(ut+6uux+uxxx)x+3uyy+3uzz=0.

(2)

本文着重讨论方程(1)和方程(2),利用双线性形式对有理函数解进行探索,得到的有理函数解包含有一组8个自由参数,然后利用符号计算系统Mathmatica求解出它们各自的lump解.基于所获得的lump解,对所涉及的参数进行特殊选择,并生成方程的一类特殊的lump解,并绘制这些解的图.

1 (3+1)维Boiti-Leon-Manna-Pempinelli方程的lump解

方程(1)描述了一个不可压缩的流体模型.其中u是一个基于尺度空间坐标(x,y,z)和时空坐标t的解析函数,文献[13]研究了可积的(2+1)维和(3+1)维BLMP方程的孤子解.文献[14]研究了 (2+1)维和(3+1)维BLMP方程的一种新的周期波解.文献[15]研究了(3+1)维BLMP方程的Wronskian行列式解.本文中研究(3+1)维BLMP方程的解.

第一步，做一个Cole-Hopf变换，

u(x,y,z,t)=-(lnf(x,y,z,t))x，

(3)

那么方程(1)变为如下双线性形式，

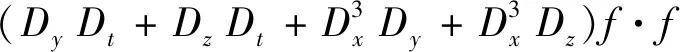
(4)

第二步，为了寻找有理函数解,设

(5)

其中ai，1≤ai≤11为待确定参数.

第三步，将(5)带入到双线性形式(4)中,借助Mathmatica,提取各项系数,可以得到一个代数方程组,从而可以确定以下代数方程组的各项系数.

常数项

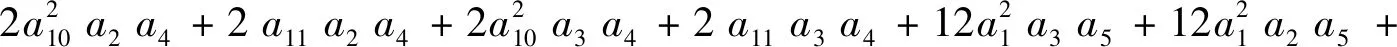
t的系数

t2的系数

x2的系数

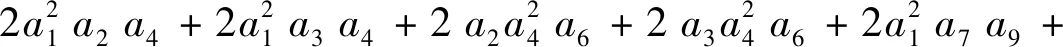
y2的系数

z的系数

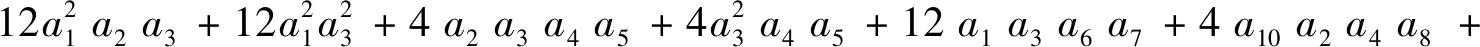
tz的系数

z2的系数

x的系数

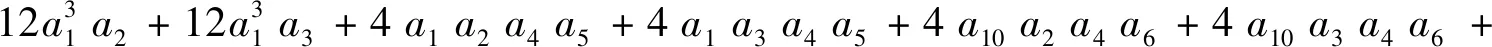
xt的系数

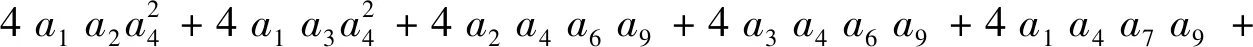
xy的系数

xz的系数

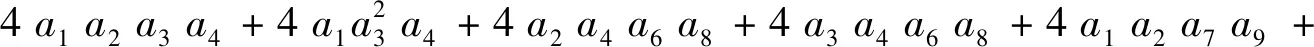
y的系数

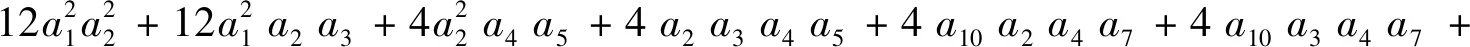
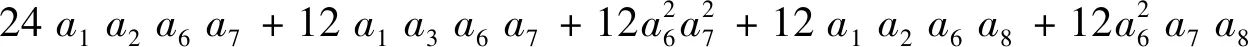
yt的系数

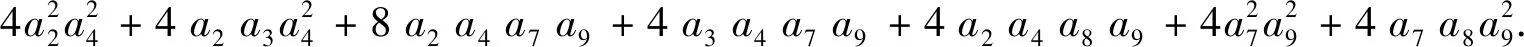
yz的系数

令常数项以及所有系数为零,借助符号计算系统Mathmatica得到一组由15个代数方程组成的代数方程组,从而得到一组解.因此

a1=a1,a2=-a3,a3=a3,a4=a4,a5=a5,a6=a6,a7=-a8,a8=a8,a9=a9,a10=a10,a11=a11.

通过变换(4),方程(1)的有理函数解如下

(6)

其中，

(7)

很容易证明x2+y2→∞,u(x,y,z,t)→0,∀(z,t)∈R2,因此得到的有理函数解为lump解.

根据(3+1)维BLMP方程的lump解描绘出三维图(图1)和等高线图(图2).其中，

a1=2,a3=-1,a4=5,a5=0,a6=4,a8=-7,a9=2,a10=0,a11=2，z=10.

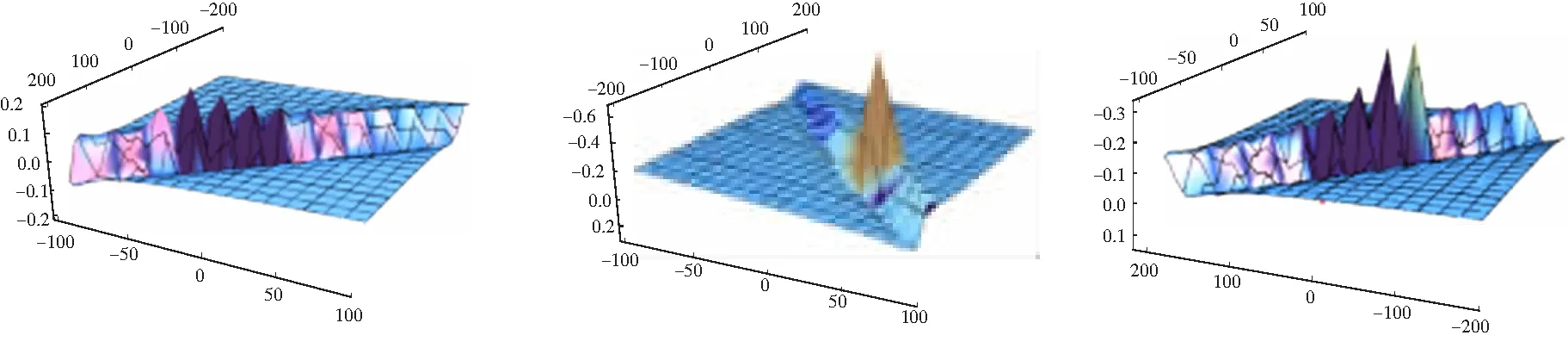
图1 BLMP方程的三维图t0=-5,5,0

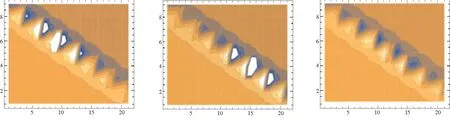
图2 BLMP方程的等高线图t0=-5,5,0

2 (3+1)维非线性发展方程的lump解

接下来,我们用同样的方法构造方程⑵的lump解.做如下变换

u(x,y,z,t)=2(lnf(x,y,z,t))xx，

(8)

从而可以得到双线性形式

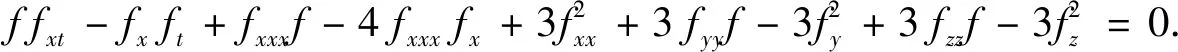
(9)

为了得到有理函数解，设

(10)

其中，ai，1≤ai≤11为待确定参数.

将(10)代入(9)中,得到

a1=a1,a2=a2,a3=a3,a5=a5,a6=a6,a7=a7,

a7=a7,a8=a8,a10=a10,

其中，2a1a2a6a7+2a1a3a6a8≠0.因此得到

(11)

其中，

很容易证明x2+y2→∞,u(x,y,z,t)→0,∀(z,t)∈R2,因此得到的有理函数解为lump解.

接下来,根据(3+1)维NLEE方程的lump解描绘出三维图(图3)和等高线图(图4).其中，

a1=1,a2=-2,a3=3,a5=0,a6=5,a7=-1,a8=2,a10=0,z=10.

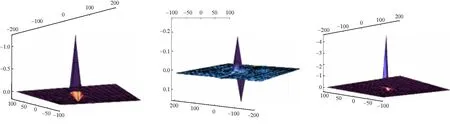
图3 NLEE方程的三维图t0=-5,5,0

图4 NLEE方程的等高线图t0=-5,5,0

3 结论

lump解是一种非奇异有理解,它在空间上所有方向都趋于零,能合理地解释相关的物理现象,并且可以描述海洋学、光学、力学等领域中的非线性波动现象.而(3+1)维Boiti-Leon-Manna-Pempinelli方程和(3+1)维非线性发展方程也是数学物理中的重要方程,因此对于寻找它们的lump解具有十分重要的意义.本文利用符号计算系统Mathmatica以及双线性形式得到了(3+1)维Boiti-Leon-Manna-Pempinelli方程和 (3+1)维非线性发展方程的lump解.

本文分析了lump解的局部化特征和能量分布,并对其进行了进一步的讨论.虽然它们所获得的lump解参数不同,但它们的形式是相同的.我们期望这些解可以在其他领域中找到.同时,我们还可以在假设有理函数解的过程中加入一个指数函数项,用同样的方法进一步构造lump-link解.