挖掘习题价值 彰显教学功能

甘肃省民乐县职业教育中心学校

费安学

1 引言

波利亚认为：“数学中，好的问题就如同雨后的蘑菇，扎堆生长，发现一个后就能在其周围发现好多个.”同样，一道好的习题是很多好试题的“母胎”.纵观当下的高考试题，不难发现，不少试题都是将教材中经典习题进行加工、拓展、综合之后而形成的.那些标新立异的试题，无不提示我们要立足于教材，深挖经典习题的内涵与外延，彰显习题的教学功能.

为了提高教学成效，课后教师都会布置一定量的习题以巩固课堂知识，帮助学生深化对概念、定义等的理解，为数学解题技巧的形成与思维能力的发展奠定坚实的基础.为此，笔者从挖掘习题价值、彰显教学功能的角度谈一些具体实施措施，以期给读者带来帮助.

2 纵向挖掘，凸显深度

教材是教学的根本，是学生赖以学习的依据.而教材中的习题不仅具有范例功能，还具有特殊的弹性特征，它能满足不同层次水平学生的学习需求.众所周知，高中数学相对比较抽象，只有立足于教材中的习题，对它们进行挖掘与二度开发，才能实现创造性地灵活使用，从而实现习题的教学功能，使学生在解题中不仅获得知识，还能获得习题中所蕴含的数学思想.

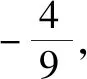
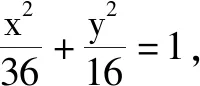
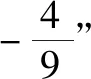
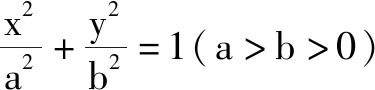
师：说说你们组的证明过程.

师：很好！如果a=b>0，会有什么新的结论呢？

生：可以获得“圆的任意一条直径所对的圆周角均为直角”的结论.

师：很好！请其他组说说你们的讨论结果.

师：说说你们的证明思路.

…………

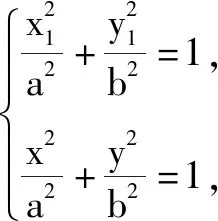
3 变式训练，灵活思维

习题对巩固知识，训练学生的思维、操作，创新等数学综合能力的形成与发展有着得天独厚的优势.但习题并不是做得越多越好，做一道题，通一类题才是解题的真正意义.为了充分发挥习题的作用，教师可在学生自主解题的基础上，以原题为第一颗“蘑菇”，将变式作为附近的一串“蘑菇”，以深化学生的理解，建构更加完整的知识体系.

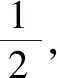
分析：观察此题，可得点N满足方程(x+1)2+y2=4，它的轨迹是圆心为(-1，0)，半径为2的圆.(解题过程略.)

为了拓展学生的思维，深化学生对这部分知识的认识，且获得灵活的解题技巧，笔者以例2为母题，拓展出几个变式供学生思考.

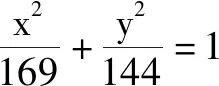
分析：此变式与原题大同小异，学生解题毫无障碍，可解得点N的轨迹方程是x2+y2+26x+25=0(过程略)，点N的轨迹为一个圆.此变式的目的在于让学生初步适应变式训练，其最大的教学价值在于让学生发现两者之间存在的共性部分，这两个问题都是知道一个动点到两定点的距离之比，求动点的轨迹方程.在掌握解题技巧的基础上，可鼓励学生继续拓展思维，将本题进行新的变式转化.

变式2求在同一平面内，到两定点A与B的距离的比为正常数λ(不等于1)的点N的轨迹方程.

分析：本题可以看成例2和变式1的一般化形式.可设N(x，y)，AB=2n，以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系.

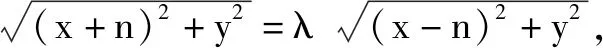
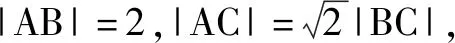
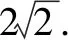
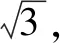
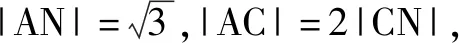
变式2根据问题的共性部分引申出“阿波罗尼斯圆”，该定义对接下来的变式训练3,4起到至关重要的作用.学生在解题过程中，深刻认识到通过变式训练的思考与解答，能达到举一反三、触类旁通的效果.因此，将习题进行灵活地变式，能有效地训练学生的思维，彰显习题的教学功能.

4 结语

总之，教材中呈现的习题都是经编者精挑细选而来，具有较强的典范性.尤其是一些起点低，看似貌不惊人的经典习题，往往蕴含着非常重要的数学思想.因此，教师应多琢磨教材中的习题，在原有的基础上进行适当的挖掘、变形或改编，充分发挥习题的教学功能，以帮助学生提升数学思维，真正达到“低起点、高落点”的功效.