高速铁路路基模型槽振动压实过程动力响应分析

蔡德钩 苏珂 安再展 闫宏业 尧俊凯

中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081

随着高速铁路列车营运速度的增加，运营过程中列车的安全性、平顺性等问题愈加突出，而高速铁路路基作为基础结构与高速铁路列车运营安全直接相关，因此铁路路基的结构质量安全尤为重要。孙天洲、刘雅欣［1-2］通过现场试验与室内试验分析了振动压实过程中含水率对粗粒土压实状态的影响，认为粗粒土的含水率处于最佳含水率附近时路基压实质量控制指标能较好反应路基压实质量。黄强、陈世豪［3-4］开展室内表面振动击实试验与大型粗粒土静三轴仪分析细颗粒含量对压实状态及累计变形的影响，定量描述了细粒含量与土体结构及长期累计变形的关系。苏建辉、朱俊高［5-6］通过多组室内试验和现场试验提出振动持时、配重及压实工艺对粗颗粒土最大干密度的影响较大。赵明华等［7］通过室内试验的方法对填石料分层进行振动压实，认为随着振动压实遍数的增加，填石层的沉降量增加，压实度提高，但当沉降量达到一定值以后，即便振动压实遍数继续增加，填石层的沉降量出现减少的情况，压实度降低。王益栋［8］以粗粒土填料为对象开展室内试验，运用数值模拟与分形理论，对颗粒破碎的强度和变形特性进行了分析和研究，验证了颗粒破碎的分形模型，揭示了分维变化的机理，进而建立了单颗粒压缩破碎强度和一维压缩变形的分形理论。

随着我国智能压实的研究越来愈深入，现场试验已经逐渐满足不了现阶段对高速铁路路基智能填筑的要求，室内试验在模拟振动压实过程中存在与现场对应关系不足的问题，其主要原因为室内试验的边界条件为完全侧限，与现场有较大差异，此外室内模拟压实对智能填筑的发展是极其重要的。因此本文依据现场试验、有限元仿真提出压实模拟槽的尺寸及模型槽边界处理方法，以达到在能够模拟现场试验的条件下进行影响连续压实效果的多因素分析。

1 路基振动压实数值仿真模型构建

通过有限元仿真软件建立高速铁路路基振动压实模型槽数值仿真模型及基于无限元边界的路基振动压实数值仿真模型，研究在小尺寸及无限元边界的模型槽中填料、边界材料及振动压实设备的动态响应信号。高速铁路路基振动压实模型槽有限元仿真模型由振动轮、分层路基结构和模型槽边界材料三部分组成，见图1。由于在压实过程中不考虑振动轮的应力应变，振动轮设置为离散刚体；分层路基结构部分采用弹塑性本构模型，强度准则为DP（Drucker-Prager）屈服准则；边界材料为常用的泡沫橡胶等吸波材料，其物理力学参数见表1。由于振动轮与填料的弹性模量差距较大，故振动轮与填料之间的接触设置为主从面接触。振动轮的尺寸及振动参数以三一重工26 t压路机为原型建模，其中振动轮的直径为1.7 m，质量为17 t，振动频率为31 Hz，振幅为2.05 mm。模型槽中路基分为5层每层30 cm，除与振动轮接触层外其余均为压实层，最上层为待压实层（厚0.4 m），填料参数见表2。

图1 高速铁路路基振动压实模型槽数值仿真模型

表1 边界材料物理力学参数

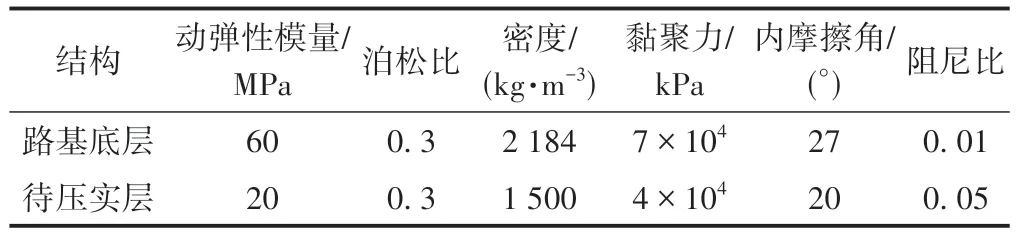
表2 路基的参数

基于无限元边界的路基振动压实仿真模型（图2）由振动轮、路基本体及无限单元组成，其中振动轮的几何建模及路基本体的本构模型和材料参数均与振动压实模型槽仿真模型一致。路基无限元边界是一种模拟真实路基的边界条件处理方法，设置目的为消除有限元固定边界条件的影响。

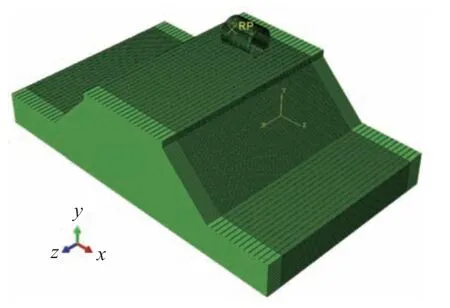
图2 基于无限元边界的路基振动压实数值仿真模型

2 室内路基压实模型槽尺寸效应分析

为对比室内路基模型槽加荷振动规律与现场路基施工的振动规律，首先分析数值模拟的振动轮、填料振动响应与现场实测振动响应，其次对比吸波边界的模型槽有限元仿真模型、足尺模型与现场路基结构数据。

数值模拟、现场实测的加速度时程曲线及频谱分析结果见图3。可知：数值模拟与现场实测加速度时程曲线形态相似，加速度幅值大致相等，为8～9g，且振动频率都为27 Hz。

图3 数值模拟、现场实测的加速度时程曲线及频谱分析结果

基于无限元边界的路基振动压实仿真模型得到振动波的加速度幅值，见图4。可知：加速度在水平方向和垂直方向上周期波以椭圆形传播，振动波在高速铁路路基内以椭球的形式在三维方向传播。因此以水平和垂直方向上角速度幅值的衰减率为90%为室内模型槽的深度和宽度，可较大程度消除边界条件对填料振动响应的影响。

图4 三维方向上加速度幅值

高速铁路路基室内模型槽尺寸设计重点为模型槽的深度及宽度，即与压路机行进方向的垂直方向。因此开展高速铁路路基波动场的现场试验，通过在振动压路机行进的垂直方向上布置传感器，检测在振动压实过程中不同位置上的加速度，得到峰值加速度幅值沿水平方向的衰减曲线，见图5。可知：峰值加速度幅值在水平方向衰减极快，沿宽度方向水平1m 位置加速度幅值衰减率达到90%以上。

图5 不同位置上加速度幅值衰减曲线

为探究加速度幅值沿深度衰减规律，在路基垂直方向上以不同距离布置传感器，检测在振动压实过程中的加速度，加速度幅值沿深度方向衰减曲线见图6。以此表示在路基压实过程中动力响应在不同施工车道方向的衰减曲线。由图6 可知：以峰值加速度幅值在垂直方向衰减较快，在路基深度1.5 m 位置加速度幅值衰减率达到90%以上。

图6 填料中加速度幅值在垂直方向上衰减

模型槽的尺寸主要考虑因素有振动轮的宽度及振动波峰值加速度幅值衰减范围。振动轮的宽度主要影响模型槽的宽度，模型槽的理论宽度由振动轮的宽度与2 倍水平峰值加速度幅值90%衰减范围组成。而垂直峰值加速度90%衰减范围主要影响模型槽理论设计深度。此外，由于模型槽宽度方向可设置弹性模量较小、密度较低吸波材料，而模型槽底部边界需承受振动轮的自重及振动轮竖向激振力因此无法设置吸波材料，因此在设计模型槽深度时需要一定余量距离以减少振动波在模型槽底部反射量。

综上所述，在振动压路机现场工作过程中在高速铁路路基剖面方向上的衰减率为90%的范围为4.0（宽）× 1.5（深）m。因此初步判断模型槽的宽度为4 m、深度为2 m。

3 模型槽边界效应分析

为分析模型槽边界材料对填料动态响应的影响，设置模型宽度方向边界材料的厚度为20 cm，三维方向上的加速度见图7。可知，①振动波未传播至边界时，振动波以椭球形沿深度方向传播，而振动波传播至边界时，由于边界材料弹性模量和密度都较低，边界材料的加速度呈无规律状态。这也表明模拟得到的泡沫板具有一定的吸波作用。②振动波在模型槽底部的橡胶边界有明显的反射现象，反射波由底部橡胶边界产生并经过于模型槽的泡沫边界最终于自由边界交界处消散。

图7 模型槽数值仿真加速度云图

无边界材料、泡沫边界材料及无限元边界模型槽填料位置加速度时域分析、频域分析结果见图8。可知，泡沫边界材料与无限元边界加速度时程曲线形态与振动轮加速度时程曲线毛刺较少，而无边界处理的填料加速度时程曲线毛刺较多。泡沫边界材料与无限元边界加速度信号频谱范围在0～100 Hz，而无边界处理的填料加速度信号频谱范围在0～200 Hz，有明显的频谱放大效应。

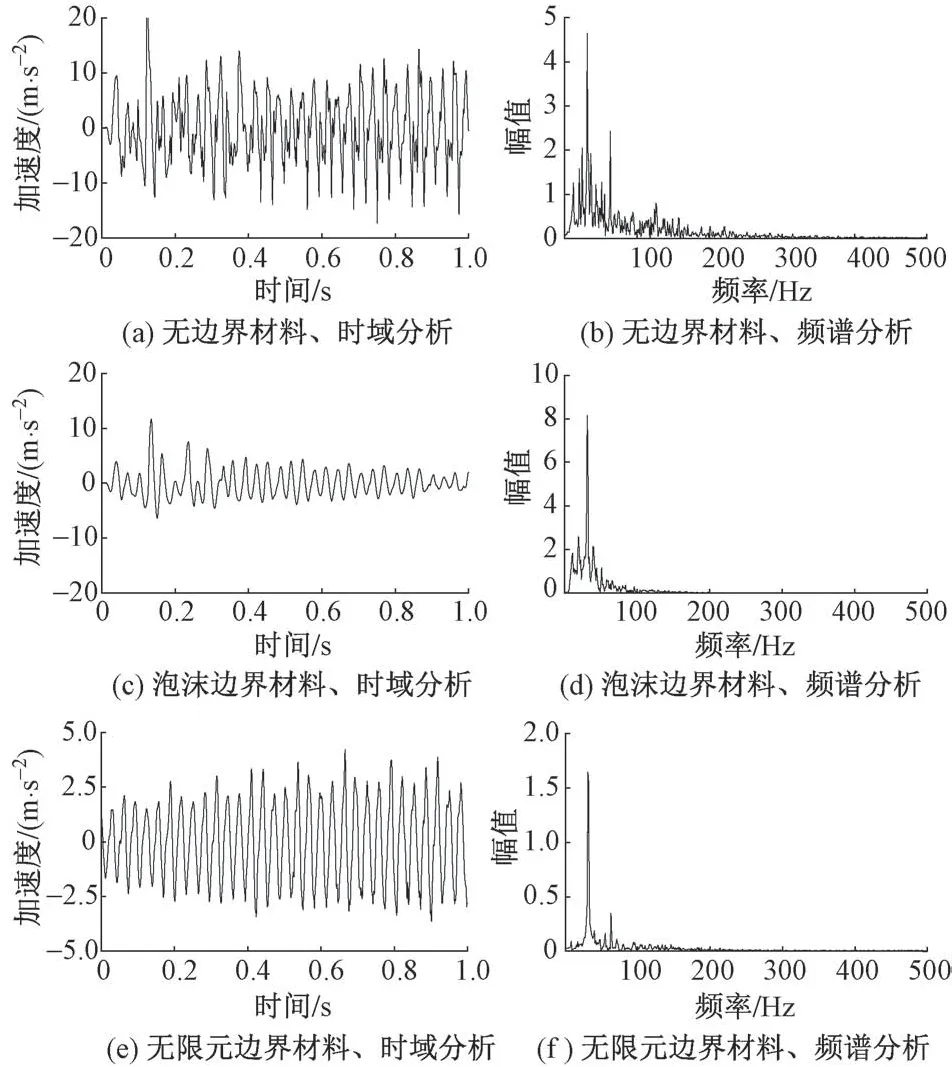
图8 泡沫边界、混凝土边界及无限元边界填料加速度时程曲线与频谱分析结果

综上，由振动轮产生的振动波从填料中到边界材料中，填料中加速度信号频谱范围会出现加宽现象；振动波由边界材料中反射至填料中时，填料中的加速度信号的频谱范围会出现二次加宽现象。

为对比低弹性模量及低密度的吸波边界材料与无边界处理的混凝土边界的吸波效应，对振动轮的正下方的测点及边界材料附近填料节点的振动响应进行时域分析与频谱分析，见图9。可知：由于振动轮振振动方向为竖直方向，振动波在试验槽底部一定会有反射波，若振动波不经过反射那么填料中的加速度幅值随着深度的增加而减少，而图9（c）中加速度幅值出现了底部的加速度幅值大于深度较小的加速度幅值的现象，因此振动波在模型槽底部发生了反射。试验槽底部加速度信号的分布范围比较广，在0～500 Hz，而吸波材料边界填料的频率分布在0～200 Hz，并没有出现边界材料中的振动波发生反射的现象。因此本文认为将模型槽底部布置橡胶边界，在模型槽宽度方向布置低弹性模量及低密度的泡沫边界材料满足室内实验要求。

图9 混凝土边界、底部橡胶的振动响应分析

4 结论

1）现场振动压实过程中路基剖面的加速度响应幅值呈椭圆状向四周衰减，并且沿深度方向1.5 m 及水平方向1 m的位置加速度响应幅值衰减率达到了90%。

2）本文以90%的峰值加速度幅值为低反射率界限与振动轮的尺寸为依据，初步设计模型槽的宽度为4 m，模型槽的深度为2 m.

3）通过研究振动压实模型槽的尺寸效应及边界效应认为：模型槽的底部边界材料为橡胶，模型槽宽度方向边界材料为泡沫时吸波效应较好，为室内振动压实模拟提供依据。