打通任督二脉，通杀立体几何中的平行问题

胡绍队

◆摘  要：近年来，在数学高考题中，试卷结构与题型比较稳定，人教A版通常有六道大题，其中必有一道立体几何问题，可见立体几何在高考中的重要地位。但对于对新疆考生来讲，难度较大！故历年考试结果来看得分率不高，很多考生望而却步。

◆关键词：立体几何;平行;逻辑推理能力

一、知识结构梳理

1.定义：同一平面内，不相交的两条直线，叫平行线。

2.判定定理：

（1）同位角相等，两直线平行

（2）内错角相等，两直线平行

（3）同旁同角互补，两直线平行

3.性质定理：

（1）两直线平行，同位角相等

（2）两直线平行，内错角相等

（3）两直线平行，同旁内角互补

4.相关高频辅助知识点：

三角形的中位线定理：三角形的中位线，平行于第三边，且等于第三边的一半。

5.线面平行系列

（1）定义：直线与平面没有公共点，叫直线与平面平行

（2）判定定理：不在平面内的直线，与平面内的某条直线平行，则这条直线和这个平面平行

专业符号语言：a⊄α，b⊂α，a∥b，则a∥α

（3）性质定理：直线与平面平行，过此直线的平面与已知直线相交，则这条直线与此交线平行

专业符号语言：a∥α，a⊂β，α∩β=b，则a∥b

6.面面平行系列

（1）定义：两平面没有公共点，叫两平面平行

（2）判定定理：一个平面内两条相交直线分别平行于另一个平面，则这两个平面平行专业符号语言：a∥β，b∥β，a⊂α，b⊂αa∩b=M，则α∥β

（3）性质定理：两面平行，被第三面所截，他们的交线平行专业符号语言：a∥β，α∩γ=a，β∩γ=b，则a∥b

二、基本题型

1.基本定理型：此类题目要求考生知道定理是什么，并知道如何用符号语言表达定理即可，要求每位学生都要撑握的题型。

例1：已知经定的三棱锥S-ABC，M，N分别是SA和SB的中点，

求证：MN∥平面ABC

证明：因为SM=MA，SN=NB，所以MN是中位线，所以MN∥AB，又因为MN ⊄面ABC，AB ⊂面ABC，所以MN∥面ABC

2.双轨相交直接双滑式：指欲证明的线面平行中，直线线两端均在单根直线轨道上，两根轨道直线相交且两根轨道直线均与平面相交于MN两点，则直线MN即为所要找的面内线。其本质是线面平行的性质定理的应用。

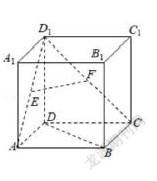
例2：如图，在正方体ABCD-A1B1C1D1中，E、F分别为AD1、CD1的中点.求证：EF∥平面ABCD;

分析：EF两点均在单根直线D1A，及DC上，且相交于D1点，两条真线分别与平面交于AC两点，符合双轨直滑式模型，故AC即为面内线，连接AC即可证明。

证明：如图，连接AC，

∵E、F分别为AD1、CD1的中点，∴EF∥AC，

EF⊄平面ABCD，AC⊂平面ABCD，∴EF∥平面ABCD.

3.双轨不交单滑式：指欲证明的直线上两点分别在两条轨道直线上，但两条直线并不相交，但均与平面相交于两点。此类题目需选择一根轨道把直线沿这条轨道滑过到平面内，结合所给条件，证明线面平行，是高考的主力题型。对考生的观察能力，推理能力，条件联系能力和综合分析能力均有一定的要求。

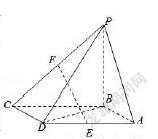
例3：如图所示，四棱锥P—ABCD的底面ABCD是平行四边形，E、F分别是棱AD、PC的中点.

证明：EF∥平面PAB;

分析：欲證的EF两点，分别在单轨道 PC及AD上，两条直线并不相交，但两条直线均与平面ABP相交，符合数学模型。在两点中，显然E点在AD这条水平标准线上，沿此直线滑向平面ABP，显然E点将落于A点，猜想F点沿水平方面右移将落于BP线段上，依据F点为CP的中点，猜想将落于BP的中点M处。故取BP中点M，形成猜想直线AM，并封口FM形成四边形，显然只需证明为平行四边形即可。即把矛盾EF与AM平行转移至FM与AE平行即可，依据两中点F，M形成的中位线，通过桥梁CB，与AD发生关系，问题得到解决。其本质依然是线面平行的性质定理的高级应用。

证明：如图所示，取PB中点M，连接MF，AM.

因为F为PC中点，所以MF∥BC，且2MF=BC

由已知有BC∥AD，BC=AD，

又由于E为AD中点，因而MF∥AE且MF=AE，

故四边形AMFE为平行四边形，所以EF∥AM.

又AM⊂平面PAB，而EF⊄平面PAB，所以EF∥平面PAB.

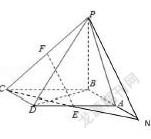
当然若选择F点沿CP滑向面内的P点，则E点较难控制（可行，但不推荐），建议使用数学化归思想把双轨不交型，巧妙转化为双轨相交型，必然要借助于P点轨道上的端点C，故，连接C点与目标点E点，并延长，使之与目标平面相交于N点，则顺利转化为双轨直滑式，故连结PN即可轻松解决问题。

方法二：

证明：如图所示，连接CE交BA的延长线于N点，连接PN.因为E为AD的中点，而AD∥BC，且AD=BC，故AE是BCM的中位线，即E为CN中点，而F是CP的中点，因而EF∥AP，又PN⊂平面PAB，而EF⊄平面PAB，所以EF∥平面PAB

通过这种系统梳理，深入浅出的把知识体系架构清楚，再辅以一定量的练习，即可有效的用科学的数学思想解决平行类问题，从而达到对核心素养的培养要求。

参考文献

[1]梁乾培，程金锋.用向量法处理立体几何中的平行、垂直问题[J].数理化解题研究（高中版），2007（04）：16-17.