基于磁极分块与转子开槽削弱永磁电机齿槽转矩

马成虎，徐余法，孙明伦，张 宙

(1上海电机学院 电气学院，上海 200240；2上海电气集团上海电机厂有限公司，上海 200240)

0 引 言

近年来，环境问题成为各国发展中不可忽略的一部分，作为可再生能源之一的风能，具有无污染、分布广泛、资源丰富等显著优势，致使风力发电得到了世界各个国家的共同关注与青睐[1]。与此同时，随着稀土永磁体的不断发展，利用永磁体代替电励磁提供磁场的永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)成为科研工作者的研究热点。由于永磁直驱风力发电机组没有齿轮箱，传动结构简单，运维成本低，可靠性高，发电效率高的优点，永磁直驱风力发电机在风电行业得到较快较好的发展[2]。

为了提高永磁直驱风力发电机对风能的利用率，对PMSM特有的齿槽转矩的削弱是永磁直驱风力发电机优化设计的关键部分。目前齿槽转矩的削弱方法主要有磁极偏移[3]，改变极弧系数[4]，不等槽口宽的配合[5]，磁极削角[6]等。文献[7-8]根据齿槽转矩对称性和周期性的特点，提出了磁极分块和磁极间隔距离对齿槽转矩的影响。前者提出将表贴式PMSM磁极均匀分块，后者在此基础上研究内置式PMSM磁极非均匀分块的方法。

本文依据文献[7]削弱表贴式PMSM齿槽转矩的思路，提出磁极分块与转子开辅助槽相结合的方法优化内置式PMSM的齿槽转矩。本文以6极72槽永磁直驱风力发电机为例，对优化前后永磁电机的齿槽转矩进行了对比，结果证明，合理的磁极分块和转子开槽相结合方法可有效降低电机模型的齿槽转矩。

1 能量法计算齿槽转矩的原理

齿槽转矩是永磁电机不通电时永磁体和铁心之间相互作用产生的转矩，是电机内部的磁共能W相对于位置角α的导数，即

(1)

式中,Tcog为齿槽转矩；W为电机磁共能；α为定子和转子之间的相对位置角。

假设电机电枢铁心的磁导率为无穷大，电机的磁场能量几乎都储存在电机的气隙和磁极之中，即

(2)

式中，B为电机的气隙磁密；μ0为真空磁导率；V为电机体积。

气隙磁密B的大小取决于电机结构尺寸与永磁体和电枢齿之间的相对位置，其沿电枢表面的分布可以表示为

(3)

式中,Br(θ)为永磁体剩磁密度；hm为永磁体充磁方向长度；g(θ,α)为有效气隙长度。

将式(3)带入式(2)并结合式(1)可得齿槽转矩的表达式为

(4)

式中,z为电机定子槽数；Lfe为电枢铁心的轴向长度；R1为电枢外半径；R2为定子轭内半径；n为使nz/(2p)为整数的一个整数；Gn为相对气隙磁导平方的傅里叶分解系数；Br为永磁体剩磁。

2 齿槽转矩优化

2.1 磁极分块方法

基于叠加法原理，电机每极的总齿槽转矩可以看作是磁极分段后每段永磁体作用的合成。总的齿槽转矩可以表示为

(5)

式中,Ns为分段数；Tn为n次谐波的转矩幅值；NP为齿槽转矩在一个齿距内的周期数；Δβ为相邻两永磁分块的偏移角度。

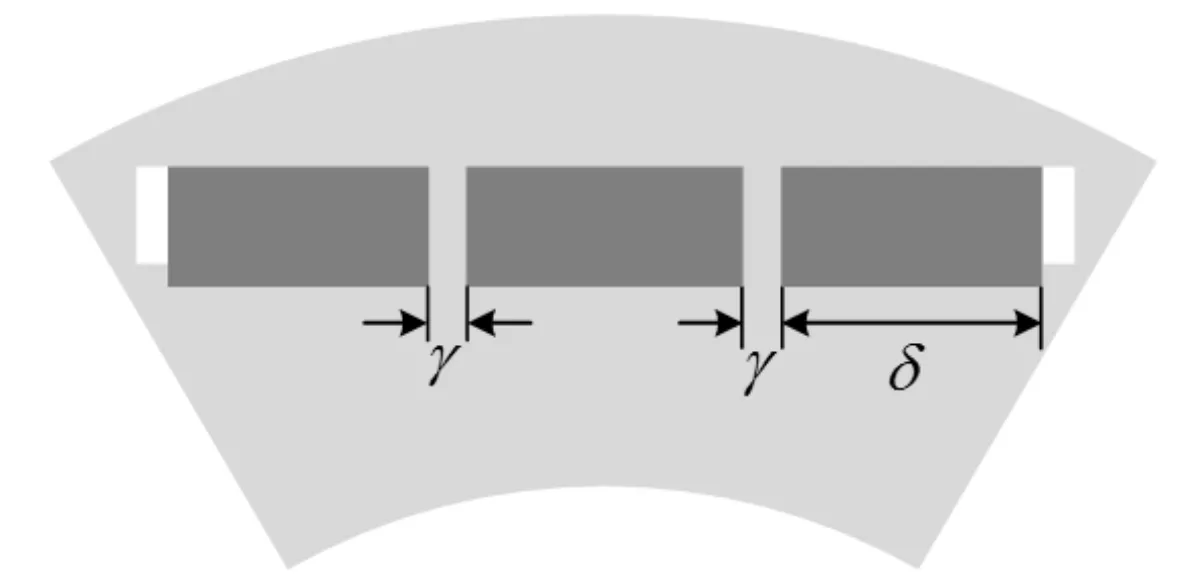
图1 磁极分块模型图

Δβ可以由图1中分块磁极的宽度δ和磁极块间的距离γ表示。

Δβ=δ+γ

(6)

由式(5)可以看出，改变永磁体的分段数Ns和相邻两永磁分块的偏移角度Δβ可以有效的削弱每极的总齿槽转矩。

2.2 转子辅助槽方法

根据式(4)可以看出，齿槽转矩的大小与永磁体剩磁密度Br(θ)的(nz/2p)次傅里叶分解的系数有关，对转子开辅助槽削弱齿槽转矩是凭借转子开辅助槽后产生的谐波来抵消电机未开槽时的谐波含量。永磁电机齿槽转矩的谐波次数是由该电机的极槽数配合决定的，即

(7)

式中,LCM(z,p)为定子槽数z和极数p的最小公倍数。

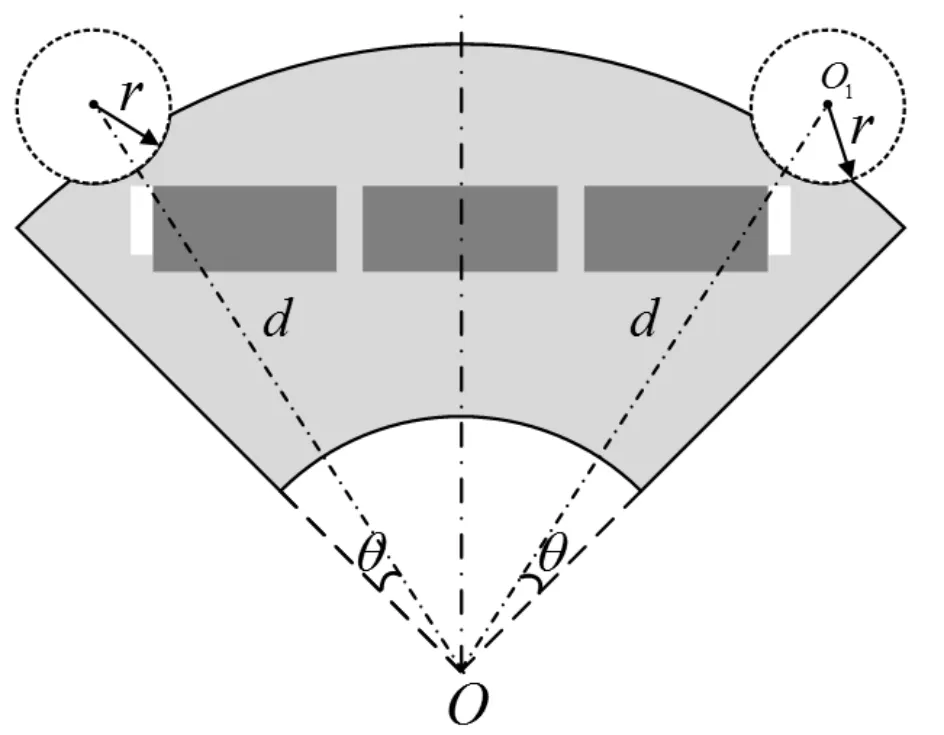
图2 转子开槽模型图

在转子上开辅助槽时，辅助槽的位置以及开槽深度需要重点研究，不合适的参数反而会增大永磁同步电机的齿槽转矩。图2为转子对称于磁极中心开弧形辅助槽模型，开槽深度由辅助圆半径r决定，辅助槽位置的改变是通过辅助圆的极弧角度θ的变化来实现。

3 有限元仿真分析

本节借助Maxwell对一台6极72槽的内置式永磁电机建模分析，设计的电机主要技术参数如表1所示。下面分两步进行验证，首先在保证永磁体用量相同的情况下，分析磁极分块数和磁极间隔对齿槽转矩的削弱效果，确定磁极分块参数后对开槽辅助圆的位置和深度进行参数化扫描分析，从而确定辅助槽位置和深度的最佳组合。

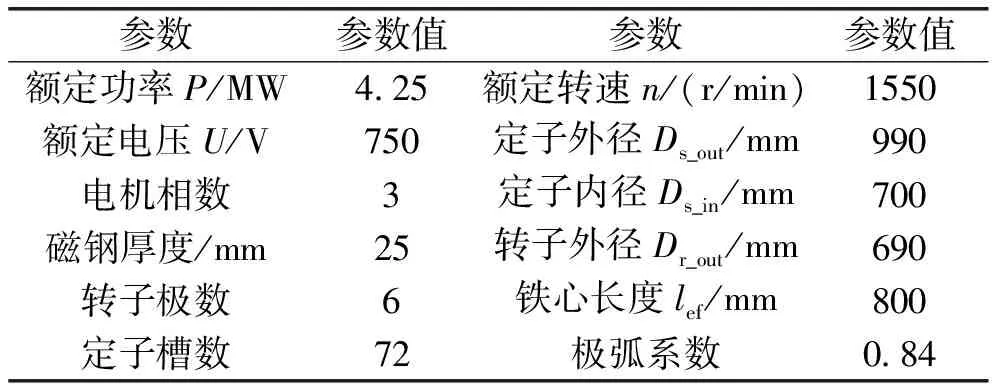
表1 电机主要参数

3.1 磁极分块对齿槽转矩的影响

由前文介绍可知，磁极分块削弱齿槽转矩是通过优化永磁体分块的数量Ns和磁极分块之间的距离γ实现的。磁极分块的前提是保证永磁体用量相同，否则会影响电机的感应电动势以及平均输出转矩。图3为永磁电机的模型，对磁极未分块以及不同分块数进行仿真分析，得出的结果如图4所示。

图3 永磁电机模型

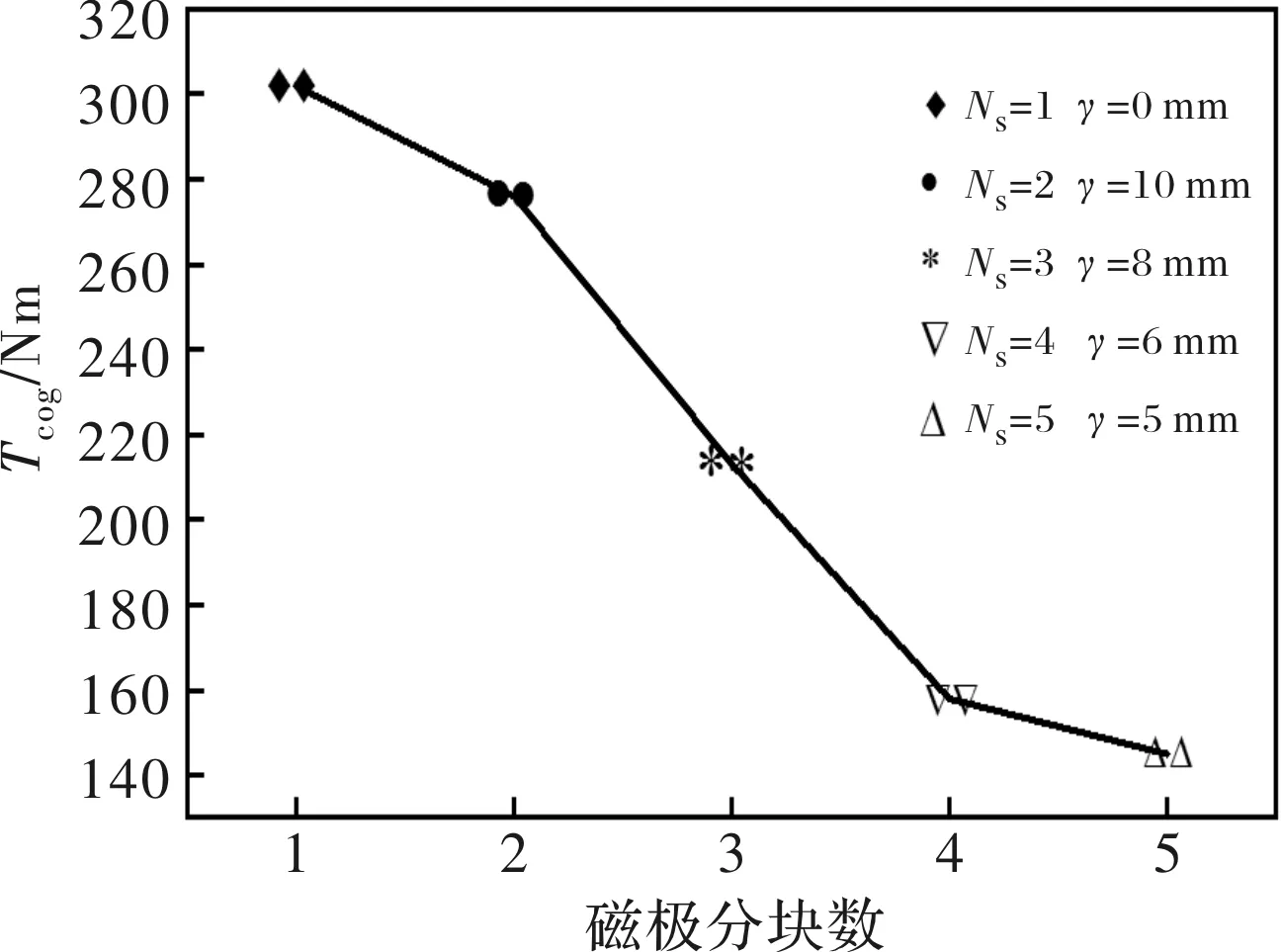
图4 磁极分块数Ns对齿槽转矩的影响

从图4可知，随着磁极分块数的增加，齿槽转矩的峰值在一直减小。磁极数为5时齿槽转矩为142 Nm，与磁极未分块时的306 Nm相比，齿槽转矩削弱了54%；与磁极分块数为4时相比，齿槽转矩的幅值相差并不大，制造成本却会明显增加。磁极间隔 对齿槽转矩影响的仿真结果如图5所示。

图5 磁极间隔 对齿槽转矩的影响(Ns=4)

由图5可知，在Ns=4的条件下，随着磁极间隔的增大，齿槽转矩先减小后增大，当γ=7.2 mm时取得最小值，齿槽转矩的幅值约62 Nm。

3.2 转子辅助槽对齿槽转矩的影响

由齿槽转矩的原理可知，通过对转子挖槽，可以减小Br(θ)的高次谐波系数，进一步削弱齿槽转矩。根据图2的方式对转子挖槽，挖槽用的辅助圆与转子圆心距d取360 mm，位置角θ取5°。利用Ansoft Maxwell仿真软件的参数化模块，对辅助圆的半径r扫描仿真，扫描范围为20 mm～30 mm，齿槽转矩随槽深变化曲线如图6所示。

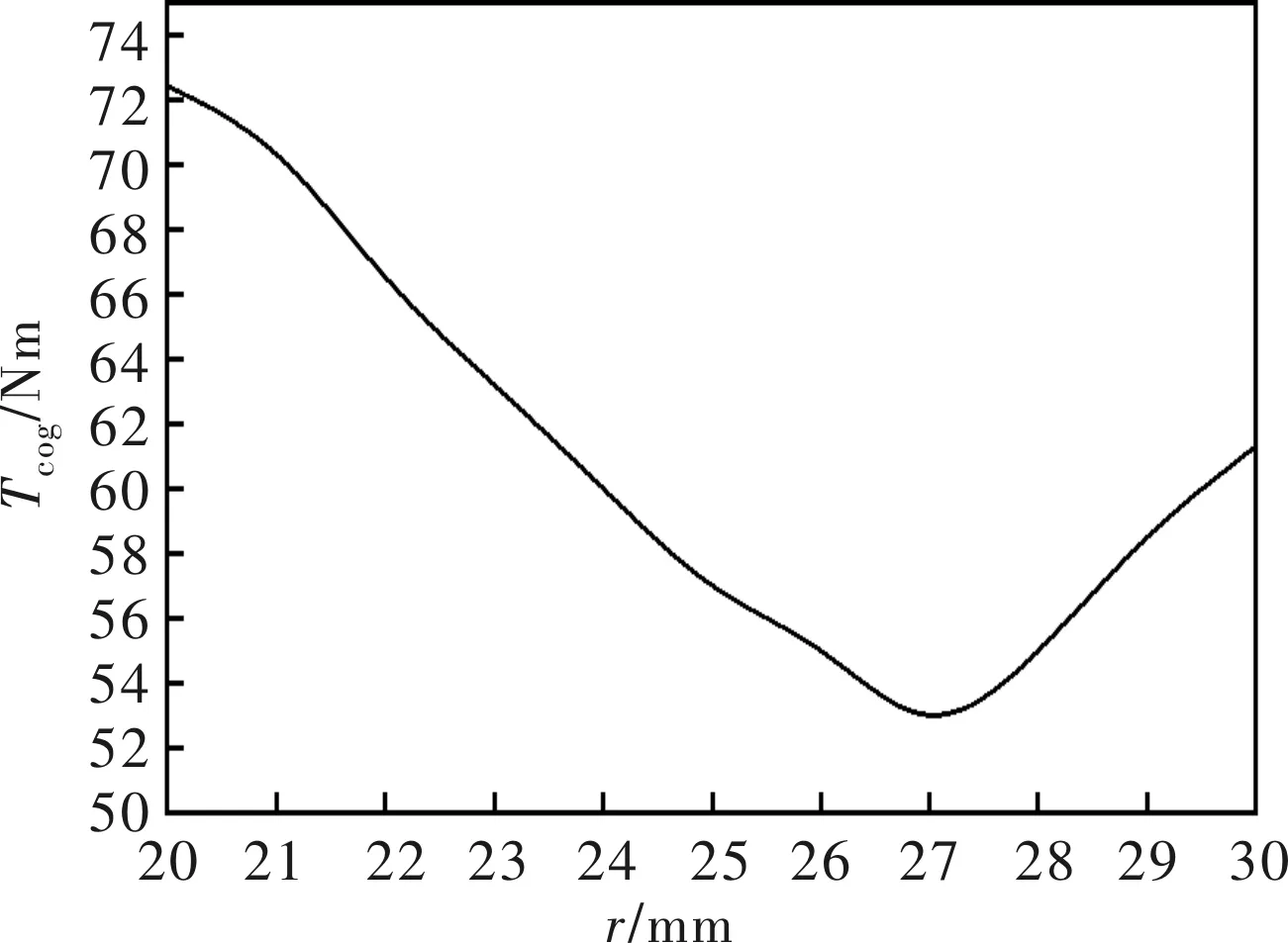
图6 槽深r对齿槽转矩的影响

由图6可知，随着槽深r的增加，齿槽转矩峰值呈现先减小后增大的趋势，在r=27 mm时，齿槽转矩取得最小值39 Nm。在此基础上进一步研究辅助圆位置角度θ对齿槽转矩的影响，θ的扫描范围为1°～7°，步长为1°，仿真结果如图7所示。

图7 极弧角度 对齿槽转矩的影响(r=27 mm)

由图7可以看出，不同位置角度对齿槽转矩的影响不同，合理的角度能有效降低齿槽转矩，而不合适的角度反而增加了齿槽转矩的峰值。齿槽转矩在θ=3°取得最小值，值为47 Nm，比转子未开槽时减小了15%。

3.3 优化前后电机性能对比

通过上述仿真分析，最终确定磁极均匀分为4块，磁极间隔取7.2 mm，槽深取27 mm，辅助圆的位置角度选择3°，并重新建立由此电机模型进行仿真。比较优化前后的电机的齿槽转矩，其结果如图8所示。

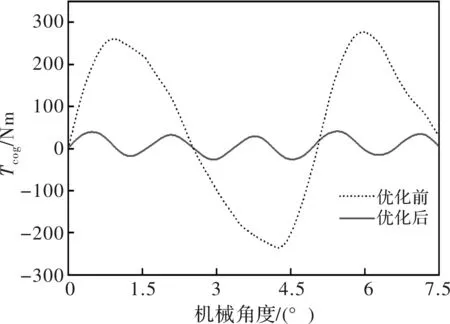
图8 齿槽转矩对比

从图8可知，通过磁极分块和转子开槽相结合的方法，永磁电机的齿槽转矩可以得到显著的削弱。与优化前相比，齿槽转矩削弱了87%，低次谐波分量幅值大幅度减小，高次谐波成为主导，齿槽转矩的周期发生变化。

电机运行性能与永磁体参数、转子结构也有很大的关系，优化后同样需要保证电机性能达到技术要求。表2为电机优化前后电机效率、线空载反电势、转矩脉动的仿真对比。

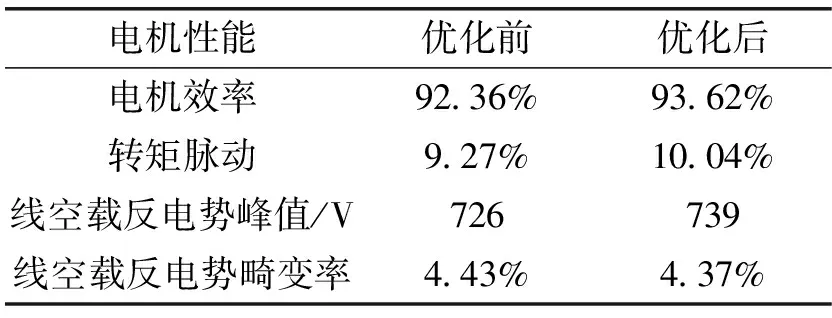
表2 优化前后电机性能对比

由表2可知，经过优化后的电机与初步设计的电机相比，电机效率以及线空载反电势峰值得到了提高，而转矩脉动和线空载反电势畸变率略有下降。整体来说，本文提出的磁极分块和转子开槽相结合的方法对电机其他性能影响较小，但是有效削弱了齿槽转矩的大小。

4 结 语

本文提出磁极分块和转子开槽相结合的方法来削弱永磁同步电机的齿槽转矩。通过Maxwell有限元仿真软件搭建6极72槽永磁发电机模型进行仿真验证，结果表明随着磁极分块数的增加，齿槽转矩的削弱效果不再显著；随着磁极间隔的增加，齿槽转矩先减小后增加；另外，合理的辅助槽深度和角度能有效降低齿槽转矩。最终，优化后的电机齿槽转矩减小了87%，而其他性能变化较小。