面向大规模定制的改进型AEWMAQ控制图应用研究

权政，赵玲玲，徐滨，樊树海

(1.南京工业大学工业工程系，江苏南京 210009;2.MIT Quality Information Program “Data Quality & Info Security” Lab.,Cambridge MA,USA)

0 前言

质量是企业的立足之本，是良好声誉的保障。大规模生产模式中，通过大批量生产某一产品而获得规模效益。这种生产模式能够产生大量的质量数据，质量控制图的绘制较为方便且可操作性强。然而，大规模定制生产模式中，由于单一产品生产的批量小，采用抽样的方法无法获取足够的质量数据，因此无法绘制质量控制图。

质量控制图由休哈特博士[1]于1928年提出，现阶段使用最多的是Xbar-R控制图。针对数据源不足的问题，杨旭等人[2]将样本均值、极差与总体均值、极差独立，实现小样本控制限稳定，降低了误发警报概率；苗瑞等人[3]利用概率积分变换理论，使质量特征值转化为标准正态分布而不受控于样本的μ、σ；刘祚时等[4]通过建立零件族与利用历史数据增加样本量，给出历史、实时数据的标准化方法，实现小批量生产监控；陈鑫和陈富民[5]引用贝叶斯理论，根据质量特征数据实时计算控制限，实现对生产过程的动态控制；宋承轩和吉卫喜[6]将Xbar-s与EWMA控制图联合监控，解决小规模数据对微小变化灵敏度不足的问题。赵玲玲等[7]提出EWMAQ控制图，减少了对源数据的需求量，对微小偏移也更加灵敏。

上述研究在一定程度上解决了大规模定制下质量监控问题，但未关注参数未知情况下相似产品质量数据标准化的方法以及控制图对微小、中等和较大偏移监测能力较差的问题。ROBERTS[8]于1959年提出指数加权移动平均控制图(Exponentially Weighted Moving Average,EWMA)，较休哈特控制图对微小偏移灵敏性高[9]。CAPIZZI和MASAROTTO[10]提出自适应EWMA控制图(AEWMA)，解决了常规 EWMA 控制图对中等和较大偏移不敏感的局限性问题。

本文作者针对上述问题，在产品族的基础上提出基于Q统计量的改进型AEWMA控制图，对大规模定制下产品生产过程进行质量监控，具有良好的效果。

1 基本理论

1.1 Q统计量

现有生产模式中，单一产品产生的质量特征值无相似性信息，没有建立休哈特控制图的条件。为此，DEL CASTILLO和QUESENBERRY提出Q统计量[11]，并给出正态分布下参数已知以及一个或两个参数未知情况下Q统计量的计算方法。事实上，控制图具有识别过程参数值异常的能力，Q控制图则对异常的监控更灵敏。如果将Q统计量绘制在控制限为±3σ的控制图上，就能较准确地知道当过程稳定且参数μ与σ为常数时预测点的趋势。

Q统计量要求样本特征值服从稳定的正态分布，即假设平均值和标准差是常数。这些统计量都具有正态或近似正态分布和近似独立特性，该方法利用t分布减少监控过程质量对于数据量的需求，且可较少地受控于样本量和样本分布的限制，能够较好地适应大规模定制所产生的数据量较少以及无可参考历史信息的情况。其通过公式(1)(2)进行转换：

ht=Gv(wt)

(1)

Qt=φ-1(ht)

(2)

式中:Gv(·)为服从自由度为v的t分布函数；φ-1(·)表示标准正态分布的反函数。统计量wt通过分布函数Gv转换为统计量ht，再通过标准正态分布函数的逆函数转换为Q统计量。

不同参数条件下的转换公式如表1所示，其中：μ表示分布均值；σ表示标准差；n表示子组大小；m表示样本量。在不同参数的情况，通过t分布函数、标准正态分布函数的逆函数Φ-1、χ卡方分布函数、F分布函数进行Q统计量转换。

表1 不同μ与σ参数条件下Q统计量转换公式

1.2 AEWMA

Shewhart控制图能够较准确地反映质量参数值的实际情况，具有一定的方便性与实用性。但是其灵敏度低，对微小偏移反应迟缓，无法及时发现异常值。

EWMA控制图较Shewhart控制图对微小偏移灵敏性高。EWMA统计模型如下：

(3)

Mt=Mt-1+Φ(et)

(4)

其中：M0=0；et=¯Xt-Mt-1为预测偏移量;Φ(·)为关于et的分段函数。

式中:λ∈(0,1];γ>0。当λ=1或γ→0时，AEWMA统计量退化为Shewhart统计量;当γ→∞时，Φ(et)=λet，Mt退化成EWMA统计量。AEWMA控制图实际上是Shewhart和EWMA控制图的平滑组合。确定控制图设计参数后，参数λ与γ为常量。为保证控制图的性能[12]，通常取0.1≤λ≤0.4、1.5σx≤γ≤3σx。

设v(t)=Φ(et)/et为等效平滑系数，v(t)随预测值et的变化而变化。当|et|增大时，v(t)随之增大，当|et|≤γ时，v(t)=λ。则AEWMA统计量表达式改写为

(5)

根据样本的均值与标准差，可得控制图的上控制限fUCL=μ0+L·σ0，下控制限fLCL=μ0-L·σ0。

2 基于产品族的改进型AEWMAQ控制图

基于上述理论，本文作者提出基于产品族的改进型AEWMAQ(Adaptive Exponentially Weighted Moving Average on Q-statistics)控制图。单一产品质量参数值存在数量不足以及无可参考历史信息的情况，通过相似元、成组技术等[13-16]理论形成相似产品的产品族。引用Q统计量对质量参数值进行标准化，为后续质量控制图的绘制创造条件。标准化后数据的方差独立于实际过程方差，并可使过程保持稳定。过程方差的变化可以转化为标准化后的数据在均值上的变化，它相较于未处理的数据具有稳定性和准确性的优势。与一般质量控制图相比，改进型AEWMAQ控制图能够更加准确、灵敏地对质量问题进行监控。通过Minitab对质量控制图进行仿真，提升了便捷性与准确性。在大规模定制的背景下，产品质量特征值数量较少，并且在实际生产过程中，其μ与σ通常是未知的。针对μ与σ未知的情况，给出Q统计量实时标准化具体步骤。样本数据如表2所示。

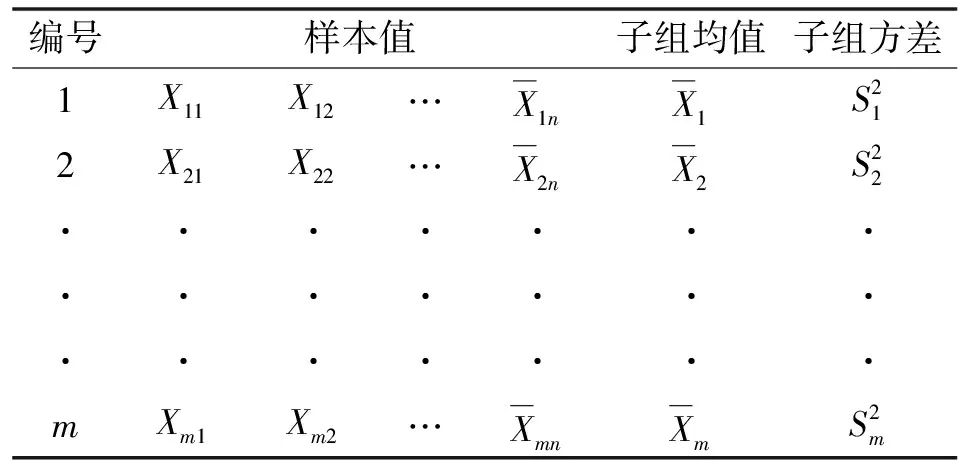
表2 样本数据

假设参数Xij～N(μ,σ2)(i=1,2,…,m;j=1,2,…,n)，则样本的均值为

(6)

(7)

样本的方差为

(8)

(9)

(10)

由于存在未知参数σ，引入卡方分布将其消除：

(11)

通过t分布，构造出不含未知参数的变量T：

(12)

变量T服从自由度为m(n-1)的t分布。为解决因为自由度的不同而使控制限不断变化的问题，求解变量T的概率密度积分h。求解过程如下：

(13)

根据概率积分变换定理,将变量T转换为Q统计量：

Q(xi)=φ-1(h)～N(0,1)

(14)

样本数据通过Q统计量标准化后，相应的AEWMA理论模型转化为

(15)

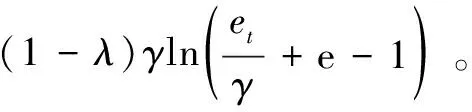
Φ(et)的表达式为

Φγ(et)=

本文作者提出的基于产品族的改进型AEWMAQ控制图，解决了源数据的处理问题，与Shewhart、EWMA控制图相比具有明显的优越性。其使用步骤如图1所示。

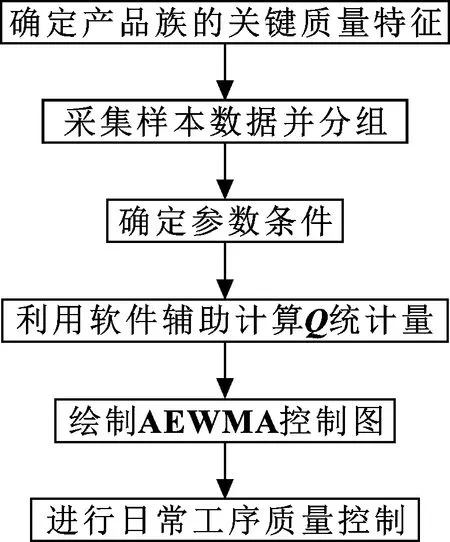
图1 控制图使用步骤

3 改进型AEWMAQ控制图应用案例

3.1 控制对象的选取

以净水器的水路板生产为例。水路板是净水器的核心物件之一，对净水器的整体质量起决定性作用。水路板由标准模具注塑而成，其质量受注塑时间、温度、环境等多种因素的影响，若直接测量水路板的力学性能，不仅会耗费额外的人力和物力，也会影响生产节拍。初步检测水路板的质量问题可采用称量其质量的方法，这种检验方法省时、简单、易操作。

大规模定制生产模式下，单一产品多为小批量生产，因此利用成组技术形成关于相似产品的产品族，收集相似产品的质量特征数据。

3.2 源数据处理

分别取AOS-S0010、AOS-S0016和AOS-S0030 三种相似型号水路板各35个质量参数值。

生产活动中，常常根据相对观测时间间隔来划分子组。子组大小n取4或5最适宜。表3所示为Q统计量标准化后的实验数据(n=5)。

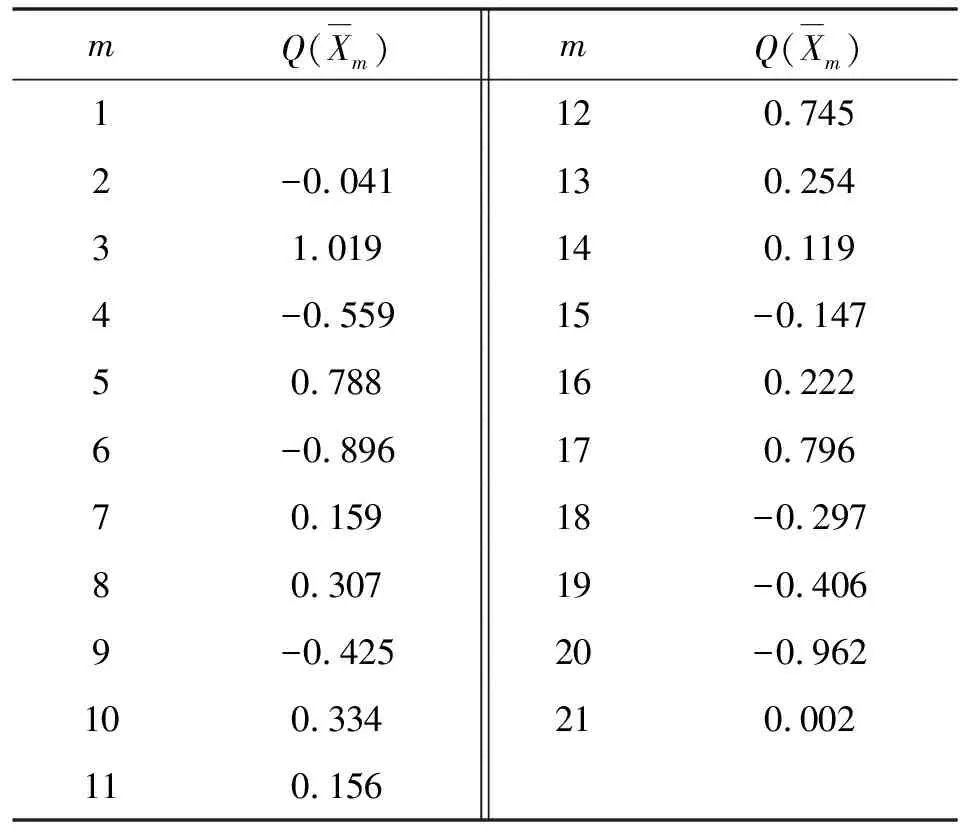
表3 Q统计量标准化后的数据(n=5)

3.3 AEWMA控制图

将Q统计量标准化后的数据进行自适应移动加权平均处理，结果如表4所示。

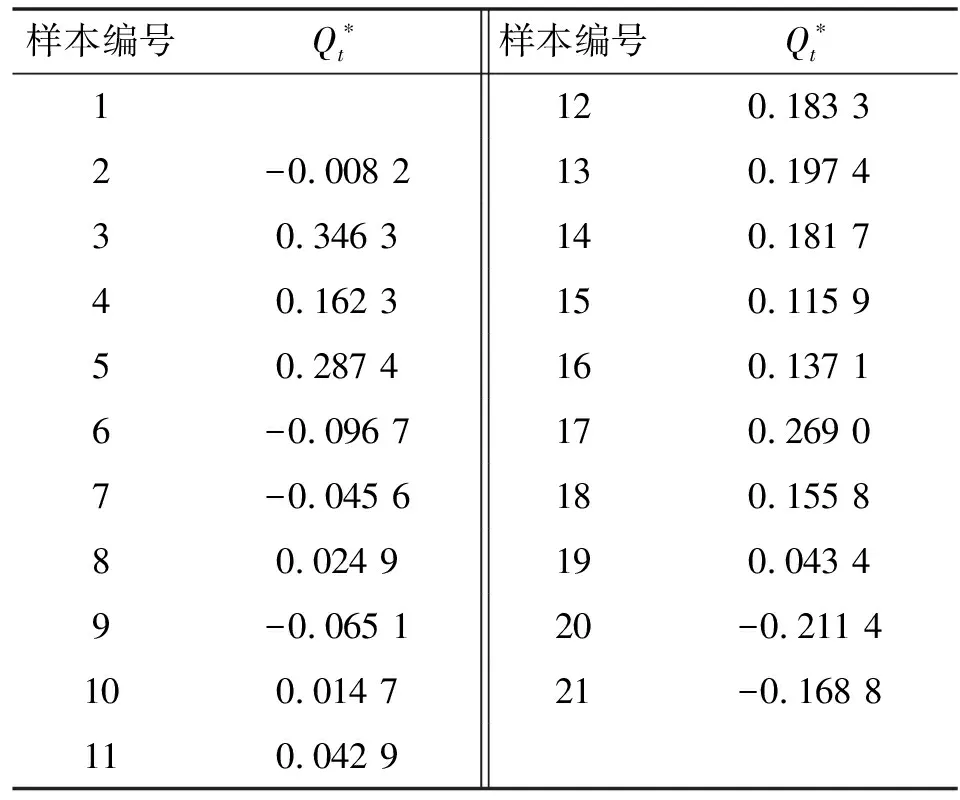
表4 自适应移动加权平均处理结果

中心线为

由于样本量较少，样本的方差采用移动极差平均值的方法估计：

(16)

式中：n表示参数数量；w表示移动极差长度，文中仿真移动极差长度取2；ε=1.128，为无偏常量。文中取最常见的L=3,以确定控制图的上下限。

控制上限：

控制下限：

图2所示为数据经过Q统计量标准化后建立的改进型AEWMA控制图。可见：样本多点靠近控制限，由此判断生产过程发生异常。

图2 改进型AEWMAQ控制图 图3 Q统计量标准化后的EWMA控制图

使用Q统计量标准化后的数据建立EWMA控制图作为对照组，标准化后的EWMA控制图处于稳定状态，如图3所示。

3.4 控制图评价

利用Q统计量对质量参数值标准化，并通过Minitab软件分别绘制改进型AEWMA控制图与EWMA控制图。由控制图的对比可以看出，两种控制图的总体趋势保持一致，但AEWMA控制图明显对中等、较大偏移更灵敏、准确性更高。

此例中EWMA控制图处于稳定状态，但是改进型AEWMA控制图有5个点位于±2σ与±3σ之间，靠近控制限。因此，控制图判异。该生产过程出现了异常，需要解决异常以后才能继续进行生产。

4 结束语

针对大规模定制下单一产品数据源不足的问题，引入Q统计量方法，对相似产品的关键质量参数值进行标准化处理。创新性地将Q统计量与自适应移动加权平均控制图联合应用，并对自适应移动加权平均模型进行改进。该方法有效解决了传统控制图与EWMA控制图的不足，实现了对大规模定制下产品质量的监控。文中给出的AEWMAQ控制图的使用步骤具有一定的实际应用价值。