基于传递函数标定法的异型盾构隧道地铁列车运行振动分析

张啟乐 董连东 刘林芽 拜立岗 马广驰 李 枫

(1.中国电子系统工程第二建设有限公司,214028,无锡；2.华东交通大学铁路环境振动与噪声教育部工程研究中心,330013,南昌∥第一作者,工程师)

单圆盾构隧道断面较小，对断面尺寸多变的区段适应能力差。最近兴起的异形盾构隧道结构断面形状较大，可同时容纳上行和下行2条线路，其在线路规划方面显得更为灵活。相关学者对异型盾构隧道的振动问题做了些探索性研究[1-3]。

现阶段地铁振动预测研究多数是完全基于有限元法。该研究方法没有对模型进行校准，故在预测过程中参数及模型假定等引入的误差不可预估。本文先现场测量振动传递函数，然后对有限元模型进行标定，并基于标定后模型对异形盾构施工隧道的列车运行振动进行分析，以期为异型盾构施工隧道的结构设计提供数据积累和经验参考。

1 振动传递函数测试

由于本文研究的线路尚未正式运营，所以选择施工车辆平板拖车作为测试目标。将隧道-土层耦合系统视为1个大的滤波系统，对施工车辆运行时隧道-土层的振动传递函数进行实际测量，并通过实测传递函数对有限元模型进行标定和校准。

现场测量的响应物理量为加速度，采样频率为1 024 Hz，数据处理窗函数为汉宁窗。测量10次过车数据取平均值作为使用数据。施工车辆在钢架支撑临时轨道上的行驶速度约为10 km/h。隧道壁测点及地面测点的振动时程和频谱如图1及图2所示。

图1 测试现场

由图2可见，信号振动加速度的峰值较多，类似于无序状态。经分析，在实测时平板车运行的临时施工轨道上，轨道接头比较多，故冲击荷载较大较多，导致振动加速度峰值较多。此外，由于施工车辆行进速度较慢，且施工车辆本身的减振系统较差，所以振动主频在10 Hz以下比较突出。

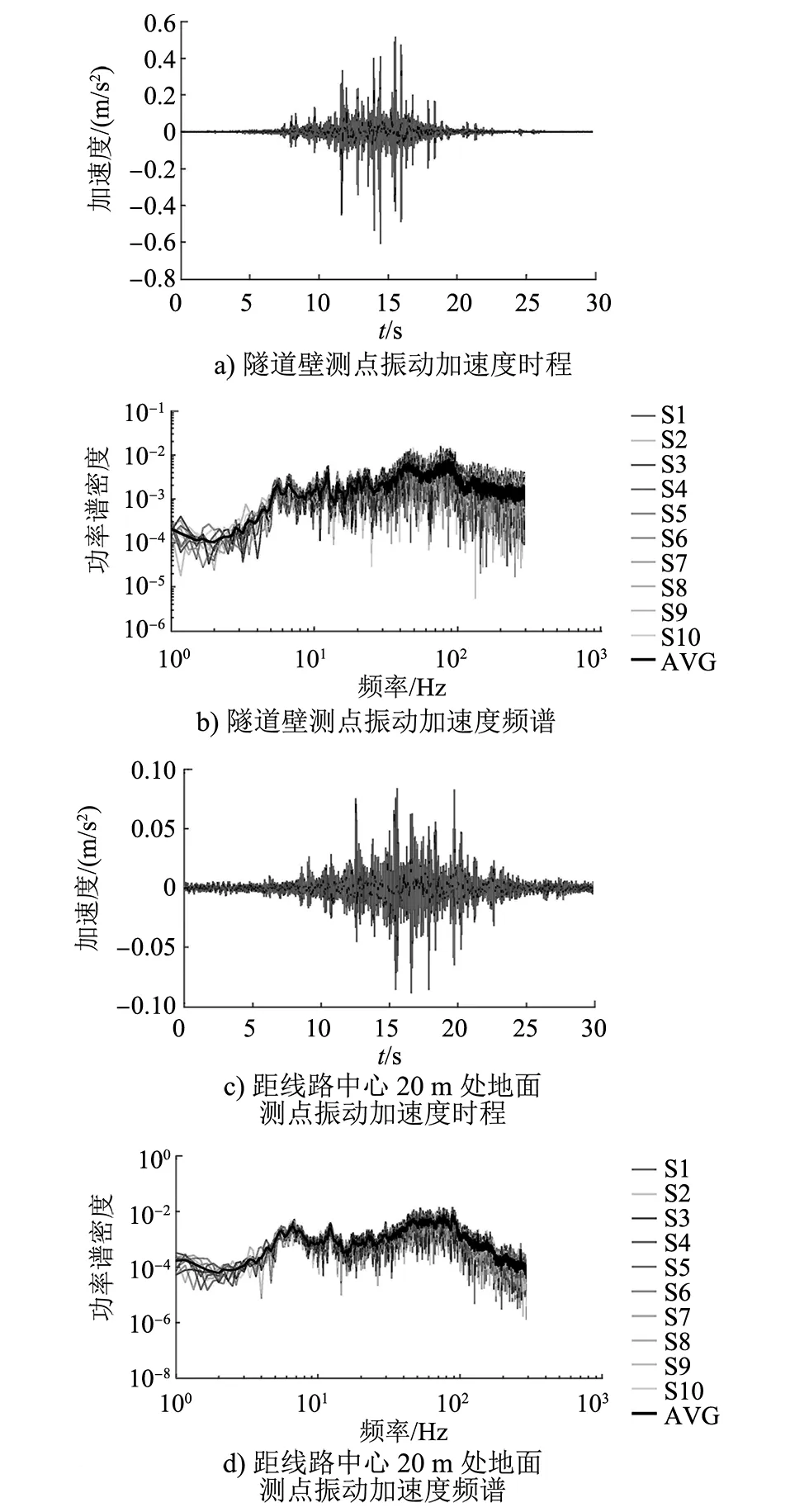
图2 振动信号时程与频谱

2 有限元模型计算

2.1 有限元模型及标定

根据地勘报告将土层等效为多个均质土层，其动弹性模量及动泊松比等可根据土层的纵波和横波波速求得。划分网格时，靠近隧道的土体网格划得较密集，而远离隧道的土体网格划得较稀疏，以缩短计算时间，并保证计算精度的可靠性。模型边界设置黏弹性人工边界，合理设置振动波的通透性，尽可能考虑所有影响结果精度的因素。有限元模型见图3。

图3 有限元模型

在隧道壁分别施加简谐荷载和测试得到的加速度时程荷载，计算两种荷载下距地面30 m处的隧道壁测点振动加速度频响函数，并与实测频响函数对比如图4所示。

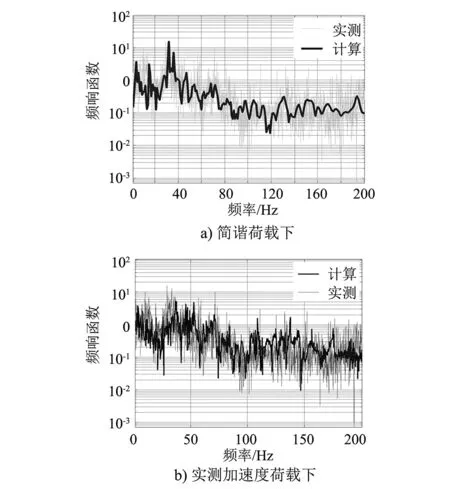
图4 实测频响函数与计算频响函数对比

由计算结果可以看出，测试频响函数和计算频响函数在各个频段均具有较好的吻合和对应，说明模型基于的假定和参数基本没有改变振动能量在各个频段的构成占比，故可以认为所采用的有限元数值模型可靠。

2.2 轮轨荷载求解[4-5]

2.2.1 实测钢轨加速度的数定求解

地铁列车的轮轨振动具有随机特性，经小波分解和重构后的钢轨加速度时程可认为是一个具有零均值的各态历经的平稳高斯过程，因此可将钢轨振动加速度波形分解为一系列不同频率的谐波。

(1)

其中，

(2)

(3)

式中：

t——记录时间；

x(t) ——根据傅里叶级数重构的加速度时程；

T——记录时长；

N——加速度波长离散点数量；

n——在0～N-1中取值；

An,Bn——傅里叶变换后的谐波幅值。

对钢轨竖向振动加速度波形进行离散采样，即将加速度波形离散成点后，有：

(4)

由式(1)～(4)，通过数学编程软件可得数定后的加速度时程。

2.2.2 基于简化列车模型的振动荷载求解

在进行地铁列车的环境振动影响分析时，主要考虑列车竖向振动，故可将列车简化为一系二系弹簧质量系统模型组合(见图5)，并设这个组合是沿隧道纵向均匀分布的。图5中,m1、m2分别为车体1/4质量及转向架1/2质量,k1、c1分别为构架的刚度与阻尼，k2、c2分别为轮对的弹簧与阻尼,P(t)为轮轨之间作用力,y0、y1、y2为竖向参考坐标系。

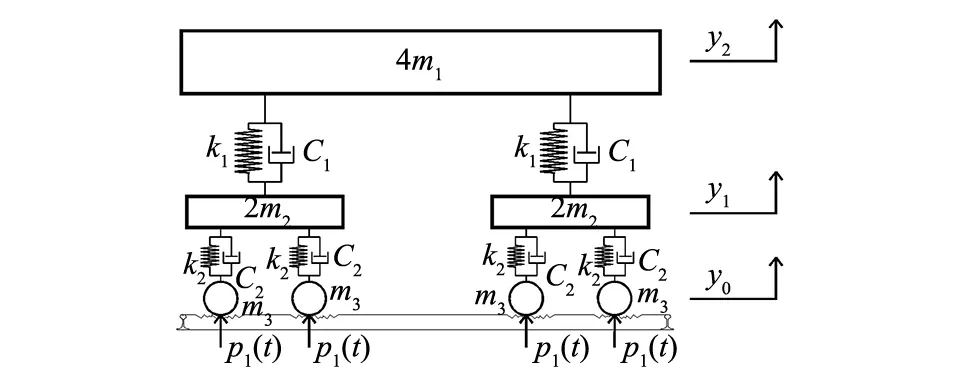
图5 地铁列车计算模型

由于列车车体重心在纵向与横向通常都是对称的，故分析单侧钢轨上的列车荷载时，可以只分析1个转向架的1侧情况。

根据图5的坐标系，利用直接平衡法建立车体的竖向运动方程。在列车正常运行过程中，若忽略轮轨之间的弹跳作用(非脱轨情况)，可以认为车轮的竖向振动加速度与实测的钢轨加速度相等。根据D′Alembert原理，仿真计算可得普通整体道床和钢弹簧浮置板道床两种情况下沿纵向均匀分布的列车线荷载，如图6所示。

图6 列车振动荷载

由图6可知：普通整体道床刚度大，整体性强，其在列车经过时的轮轨作用清晰可见；而钢弹簧浮置板道床因其依靠减小轨道系统刚度来减小振动，削弱了隧道基础与道床之间的耦合，故其振动荷载的变化无法清晰体现列车经过时的轮轨作用。

2.3 不同隧道埋深时的振动分析

在隧道埋深不同时，振动传递特性及钢弹簧浮置板道床减振效果也有差异。

2.3.1 埋深与水平距离的影响

本文基于既有土层不同埋深条件下，研究地面振动沿垂直线路方向的衰减关系。

在有限元模型中，以隧道正上方地面为坐标原点，于5 m、10 m、15 m及20 m埋深处，每间隔5 m取1个计算点。不同埋深下，地面振动与水平距离x的衰减关系如图7所示。

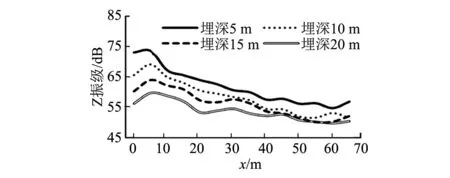
图7 Z振级沿地面衰减

当隧道埋深不同时，地铁运行引起的地面振动大致呈现出埋深越深、振动越小，埋深越浅、振动越大的规律。但这一规律并非绝对适用。不同埋深的隧道对应的地面振动放大区出现的位置不同，埋深越深，隧道地面振动放大区的x就会越大。

由图7可见，埋深增加量与Z振级衰减量不是线性关系。单就地铁环境振动控制而言，存在一个最佳经济埋深，其与地质参数、线路条件等有关。根据GB 10070—1988《城市区域环境振动标准》[6]，特殊住宅区昼间和夜间Z振级限值为65 dB。由此可知，本计算测点的最佳经济埋深为15～20 m。

2.3.2 地铁振动的传递特性

计算不同埋深时隧道壁到地面x=0、x=20 m及x=40 m处测点的振动传递损失，如图8所示。

由图8可知：30 Hz以下的低频振动衰减很慢，80 Hz以上频段的振动衰减非常快；频率越高衰减越大；在100 Hz以上有大于50 dB的振动加速度级衰减量；地铁振动是宽频振动，在各个频段均有能量分布，地铁振动传至地面时振动频率主要集中在63～80 Hz，与其他城市地铁振动测试结果结论相一致[7-8]。

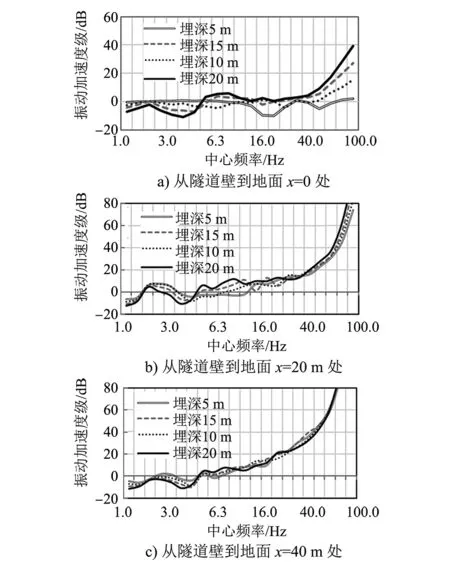
图8 振动传递损失

2.3.3 钢弹簧浮置板减振分析

在类矩形盾构隧道模型中建立特殊减振轨道结构-钢弹簧浮置板道床。假定埋深为17.8 m，分析采用钢弹簧浮置板隔振措施时Z振级沿地面的衰减情况，如图9所示。

由图9可知，采用钢弹簧浮置板道床减振系统后，地面各位置的Z振级有显著的减小，其中在线路正上方地面位置的Z振级减振量为14.6 dB，x=5 m位置的Z振级减振量为13.5 dB。

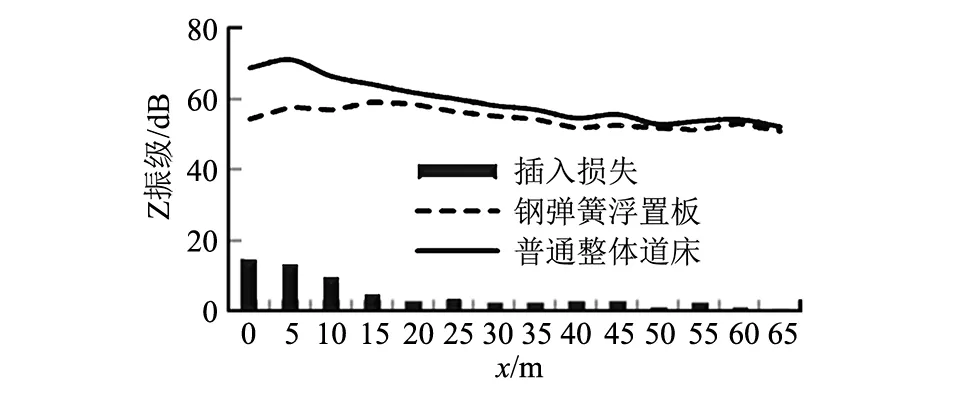
图9 地面Z振级衰减对比

2种轨道结构从隧道壁到地面的振动传递损失如图10所示。

图10 不同轨道结构的振动传递损失对比

振动由隧道壁传递至地面线路正上方的途径中：20 Hz以下低频振动的衰减不是很明显；在30～100 Hz的中间频段(相对于本频程的中间部分)，每个中心频率处整体道床和钢弹簧浮置板传递损失差值基本恒定，差别不大；在大于100 Hz的频段，普通整体道床的传递损失更大。究其原因，采用普通整体道床时，隧道壁处会产生大量高频振动，而且高频振动比低频振动衰减快。

3 结论

1) 埋深增加量与Z振级衰减量不是线性关系。单就地铁环境振动控制而言，存在1个最佳经济埋深。本算例的最佳经济埋深在15～20 m之间。

2) 地铁引起的80 Hz以上频段的振动衰减非常快，传至地面时峰值频段主要集中在63～80 Hz，80 Hz以上高频振动能量占比不大。

3) 距离线路中心线越近，采用钢弹簧浮置板后的振动插入损失越大，减振效果越好。采用钢弹簧浮置板措施后，在隧道正上方地面处的Z振级可以减小14.6 dB。