不同梯形巷道围岩应力特征及变形规律的数值模拟研究

孙宇超

(中铁十九局集团矿业投资有限公司，北京 100000)

0 引言

矿山开采过程中巷道的断面形状随矿体的赋存条件、矿体强度及地应力情况的不同存在多种形式，科学合理的断面形状可以有效地减缓围岩的应力，提高巷道的稳定性，即使遇到破碎岩层时，也可以采用适当的支护方式提高巷道的稳定性，减弱巷道的应力条件，提高巷道质量，减少支护成本。矿山在开采过程中，尤其是煤矿开采过程中，煤层的赋存条件常常呈水平或倾斜状，且倾斜煤层居多，地应力相对较大，对于倾斜煤层的巷道断面形状，主要以等腰梯形和直角梯形的方式进行布置，巷道的应力条件复杂，支护困难，时常出现片帮、顶板冒落和离层等危险情况。

近年来，许多学者对煤矿巷道断面的布置形式及支护方式进行了研究。杨旭明[1]研究了大断面煤巷巷宽效应及支护技术，提出了宽巷条件下巷道的有效支护方式，提高了巷道的稳定性。李小裕等[2]采用有限元数值模拟技术，研究了复杂采动条件下不同巷道断面形状条件下围岩的稳定性。孔祥松等[3]采用相似模拟试验，研究了南关矿煤巷在钢管混凝土支护作用下的巷道变形破坏规律。徐仁桂等[4]采用理论分析、数值模拟及工业性试验的方式，对倾斜煤层梯形巷道煤柱的合理宽度进行了研究。陈新年等[5]采用相似试验的方法，对倾斜煤层直角梯形巷道应力非对称试验进行了研究。本文在前人研究的基础上，采用FLAC3D数值模拟技术，对矿山开采过程中的等腰梯形巷道和直角梯形巷道的应力进行了研究，分析巷道围岩的应力分布情况，为今后矿山开采过程中巷道的布置方式提供了理论基础。

1 实验模拟方案

采用控制变量法[6-7]对复杂采动条件下不同梯形巷道围岩稳定性变化规律进行数值模拟研究。由于煤层赋存条件的差异，在煤层开采过程中常常以断面为梯形的巷道进行开采，根据煤层倾斜程度的不同，梯形巷道又分为等腰梯形巷道和直角梯形巷道。因此，此次研究分两种情况分别进行讨论，对于等腰梯形巷道，以巷道的顶板宽度和底板宽度的比值为研究对象，通过改变巷道的顶底板宽度的比值来分析巷道围岩的应力及变形规律；直角梯形巷道常适用于倾斜煤层，因此对于直角梯形巷道，以巷道顶板与围岩的夹角为研究对象，通过改变顶板宽度与侧帮（低帮）之间的夹角来分析巷道的变形特征，进而分析煤层在不同倾斜条件下直角梯形巷道的稳定性情况。设等腰梯形巷道的高度为5 m，顶板宽度为 4 m，顶底板宽度比例分别为 1:1.2，1:1.4，1:1.6，1:1.8，1:2.0，具体见表1。直角梯形巷道围岩低帮长度为3 m，底板宽度为4 m。顶板与围岩之间的高夹角分别为 10°、15°、20°、25°、30°，具体见表2。

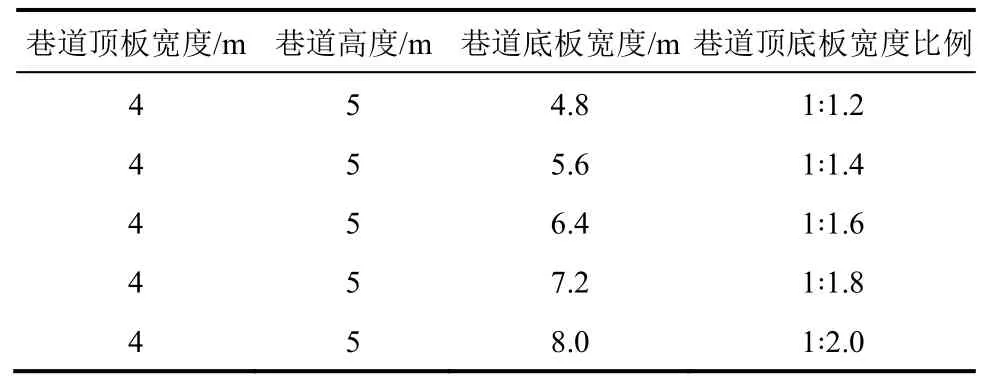
表1 等腰梯形巷道研究参数

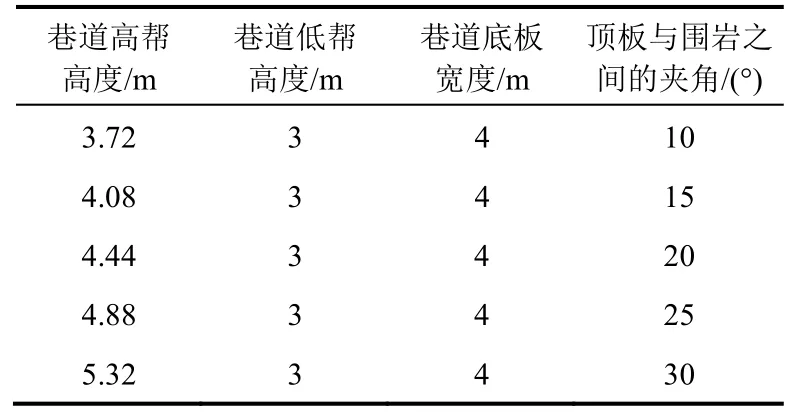
表2 直角梯形巷道研究参数

2 模型建立

由于煤层厚度相对较小，因此模型总体上分为煤层和围岩两部分。由于煤层埋藏深度较大，通常为 400～800 m，因此模型顶部施加密度为 2600 kg/m3，高度为500 m的垂直应力，侧压系数取1.2进行力学分析。鉴于此次模拟主要研究梯形巷道围岩的稳定性规律，且巷道开挖最大尺寸为5 m，工程上认为围岩开挖半径5倍以外的围岩应力对巷道的影响不足5%，可忽略不计。因此，为便于模拟运算，此次设计模型的尺寸为：长×宽×高=50 m×28.8 m×30 m，如图1所示。

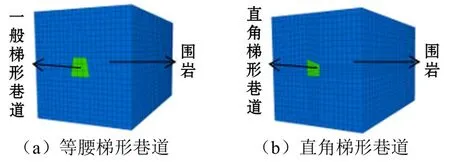
图1 模型示意（部分图件）

2.1 力学参数的选取

模拟中模型中部为巷道，周边为围岩，模拟中不区分煤层和围岩，统一以一种岩体代替，旨在更精确地分析出不同梯形巷道的围岩变形规律。根据相关文献了解得到2种岩体的力学参数，见表3。

表3 岩石力学参数

由于岩石应力-应变及变形等物理力学性质满足弹塑性材料特征，根据理论和经验，岩体破坏主要是剪切和拉伸破坏，所以此次研究选用摩尔-库伦强度准则作为材料破坏准则[6-7]。基于模型中摩尔-库伦准则的参数特点，结合表3中的岩石力学参数，可得出各岩层岩石单轴抗拉强度tσ、体积模量K和切变模量G，其公式为：

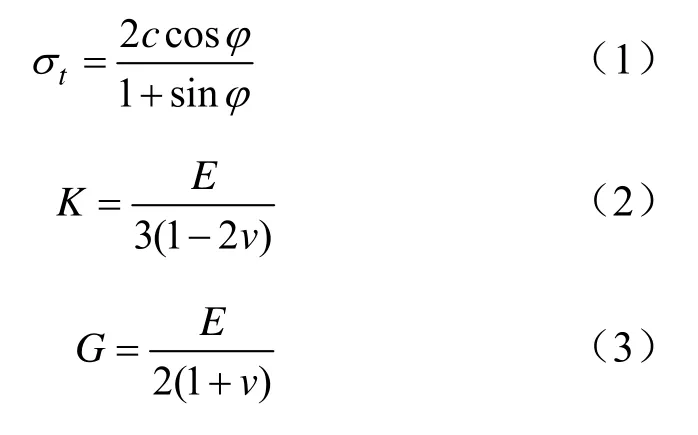
式中，E为弹性模量；v为泊松比；c为内聚力；φ为内摩擦角。

2.2 边界条件

边界条件包括位移边界和应力边界，其中应力边界指垂直应力和水平应力，研究中模型顶部施加密度为2600 kg/m3，高度为500 m的垂直应力，水平应力根据侧压系数为1.2进行计算。经计算得水平应力为6.35 MPa，垂直应力为7.62 MPa。位移边界为约束模型水平和竖直方向上的位移边界，在模拟过程中，需作如下假设：

（1）各岩层均为各向同性的均质体；

（2）符合摩尔-库伦弹塑性理论模型；

（3）模拟过程中不考虑地下水、节理裂隙和时间效应。

3 结果分析

3.1 模拟结果

根据模拟方案，计算得到等腰梯形巷道和直角梯形巷道在不同条件下的应力情况，其中，等腰梯形的水平应力云图如图2所示，直角梯形的水平应力云图如图3所示。

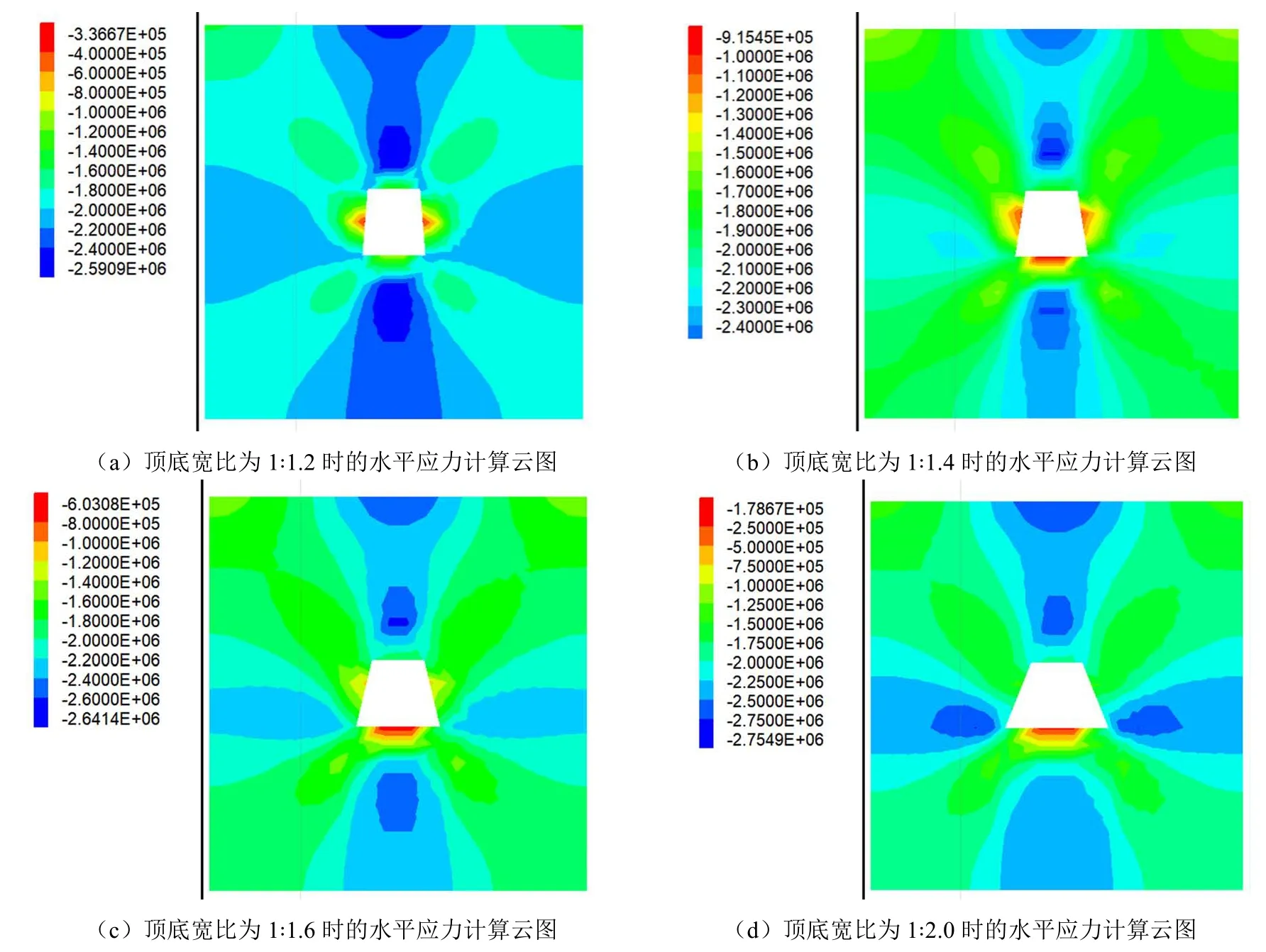
图2 等腰梯形巷道部分不同顶底宽比的巷道水平应力模拟云图

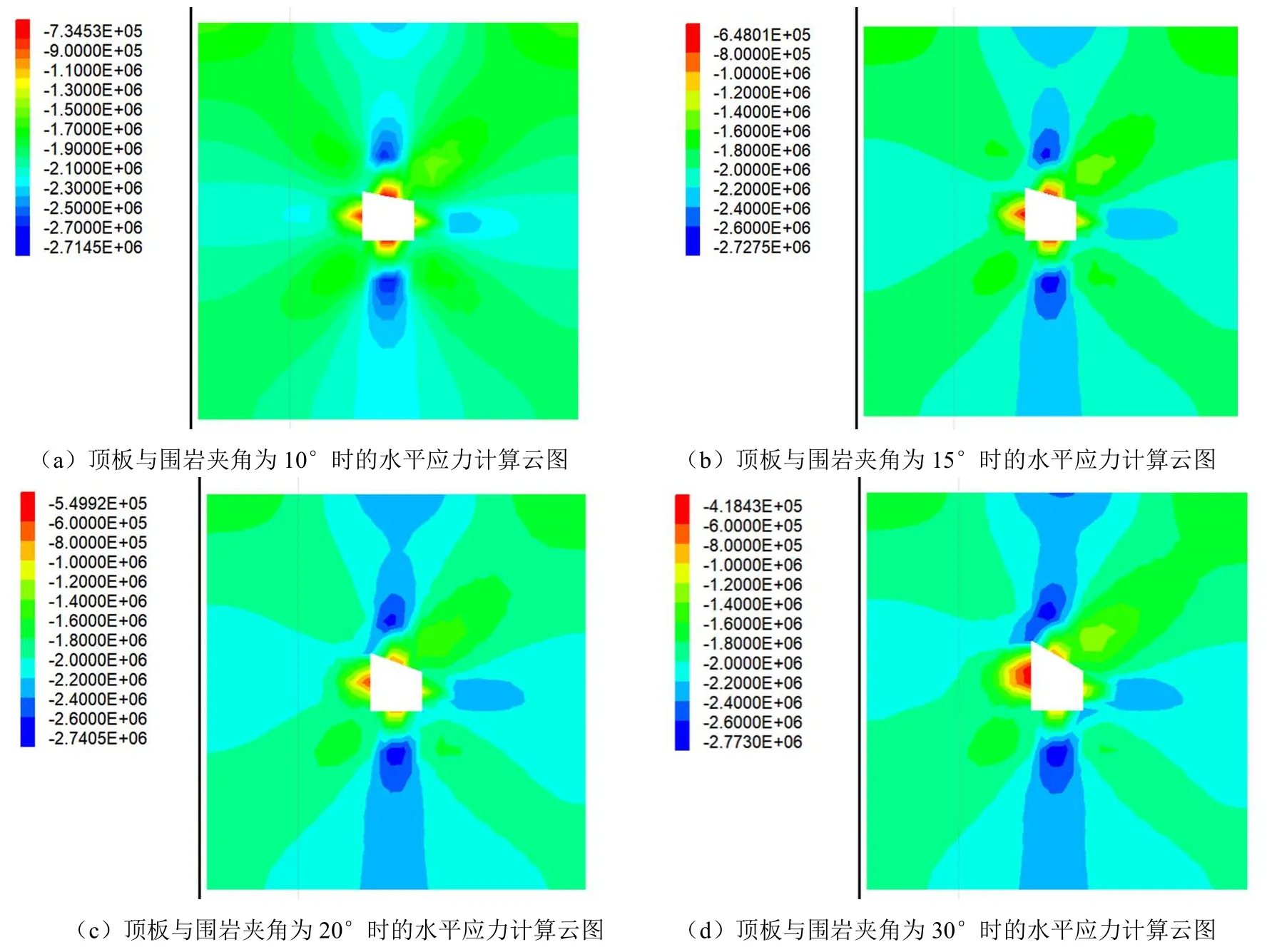
图3 直角梯形巷道部分顶板不同倾角下的水平应力模拟云图

将 FLAC3D数值计算结果导入 Origin[8]后处理软件，分别得到等腰梯形巷道和直角梯形巷道垂直应力、水平应力和最大主应力的对比结果（见图 4和图5）。

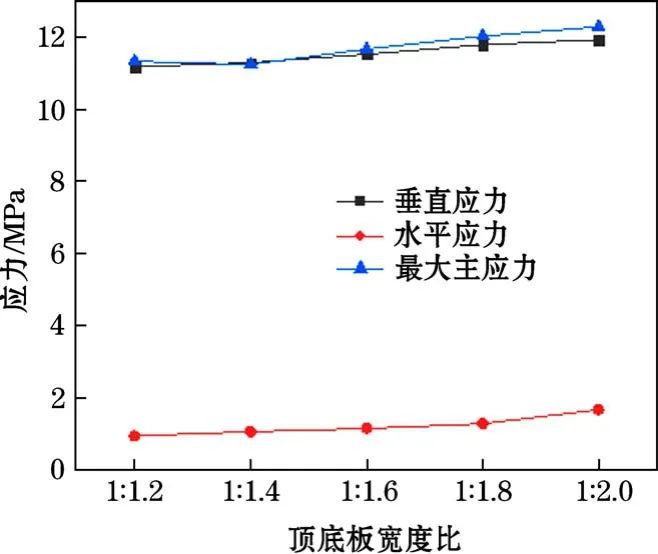
图4 不同顶底宽比等腰梯形巷道周边应力对比

图5 直角梯形巷道不同顶板夹角条件下巷道周边应力对比

3.2 数据分析

根据图2可知，等腰梯形巷道随着梯形巷道顶底宽比例的增加，巷道周边的水平应力逐渐向巷道底板转移，巷道周边的应力呈对称型分布，且巷道底板两侧边角处的水平应力逐渐增加，并在巷道底板两侧边角处产生了应力集中。因此，当矿山采用等腰梯形巷道时，要格外注意等腰梯形巷道底板两侧边角处的围岩变形及破裂情况。根据图3可知，直角梯形巷道随着顶板与低帮角度的增加，巷道周边的水平应力逐渐向直角梯形巷道高帮一侧转移，巷道周边的应力呈非对称型分布。且直角梯形巷道随着顶板与低帮角度的增加，水平应力主要集中在直角梯形巷道顶板靠近高帮一侧，并呈逐渐增加的趋势。鉴于此，当矿山采用直角梯形巷道时，应特别注意直角梯形巷道顶板高帮一侧的围岩变形情况，并在掘进中进行支护，以保证巷道的稳定性，确保掘进及回采作业的安全。

根据图4可知，等腰梯形巷道随着梯形巷道顶底宽比例的增加，巷道周边的水平应力、垂直应力及最大主应力均呈逐渐增加的趋势，且垂直应力的变化规律与最大主应力的变化趋势很接近，说明等腰梯形巷道在改变顶底宽比例的条件下，巷道周边的应力以垂直应力为主。根据图5可知，直角梯形巷道周边的水平应力无论是高帮一侧还是低帮一侧，均随着顶板与低帮角度的增加而逐渐降低，且高帮一侧的水平应力大于低帮一侧；同时将直角梯形巷道周边的水平应力、垂直应力和最大主应力进行对比发现，对巷道稳定性起决定性作用的应力为垂直应力，因此，当矿山采用直角梯形巷道时，不仅应加强巷道高帮一侧的支护，还应该加强对巷道顶板的支护，以提高巷道的整体稳定性。

4 结论

通过对等腰梯形巷道和直角梯形巷道围岩周边应力的分析，可以得出以下结论。

（1）等腰梯形巷道随着梯形巷道顶底宽比例的增加，巷道周边的应力均呈对称分布，且水平应力逐渐向底板转移，巷道底板两侧边角处为应力集中区域。

（2）直角梯形巷道随着顶板与低帮角度的增加，巷道周边的应力呈非对称分布，巷道周边的水平应力逐渐向直角梯形巷道高帮一侧转移，且巷道顶板靠近高帮一侧为应力集中区域。

（3）通过对等腰梯形巷道和直角梯形巷道周边应力的对比发现，开采过程中无论采用等腰梯形巷道还是直角梯形巷道，巷道周边的应力均以垂直应力为主，且在支护过程中，除应加强顶板的支护外，还应该加强对应力集中区域的支护，以确保巷道的稳定性。