锚杆支护路堑高边坡的稳定性及影响因素分析

王洪英

（广东省冶金建筑设计研究院有限公司 广州510080）

0 引言

边坡稳定性分析方法主要有极限平衡法和强度折减法［5］，其中以极限平衡法为代表的数值分析方法近年来在工程中得到广泛应用。期间也有许多学者和技术人员对锚杆支护路堑高边坡的稳定性分析方法及其影响因素进行了相关的研究，如董兆松［6］基于强度折减法求解了某边坡的安全系数；李振江等人［7］基于土体非线性本构模型，对锚杆加固边坡前后的应力场和位移场进行了分析，并对加固效果进行了评价；史卜涛等人［8］考虑边坡土体和支护结构的相互作用，分析了锚杆支护边坡的稳定性；林杭等人［9］基于强度折减法，采用双弹簧单元模拟锚杆，研究了锚杆对称布置形式对边坡安全系数及滑动面位置的影响。边坡稳定性计算方法还有极限平衡法，其包括瑞典条分法、毕肖普法、简布法和不平衡推力法等。我国现行《公路路基设计规范：JTG D30—2015》［10］主要推荐采用不平衡推力法进行设计。对于锚杆支护边坡，锚杆长度、水平间距以及锚杆倾角对边坡稳定性以及滑动面位置都会有影响［11-12］。为此，韩爱民等人［13］对锚杆支护边坡的设计参数进行了影响因素分析，研究了锚杆框架梁对边坡边坡稳定性的影响。熊文林等人［14］研究发现锚杆的方向角对支护效果影响较大，并给出了锚杆倾角的取值范围。总之，极限平衡法计算简单，在工程中得到了广泛应用。

基于此，本文拟在现有极限平衡法的基础上，进一步总结前人的研究成果，并以具体的工程为例，分析不同工况下锚杆支护路堑高边坡前后的稳定性；进而分析锚杆长度、水平间距以及倾角等支护结构参数对边坡稳定性的影响规律；据此提出更为合理的支护方案，以期为本工程或类似工程设计与施工提供参考。

1 边坡稳定性分析

在边坡中加入锚杆等支护结构的目的为用其承受土层自重产生的拉力或预应力，从而加固坡体的不稳定部位，建立有效支撑的工程。边坡稳定性分析的方法中，极限平衡法是目前工程中应用最广泛、最普遍的一种分析方，其主要包括瑞典条分法、简布法、毕肖普法及不平衡推力法。

1.1 未考虑锚杆支护的边坡稳定性分析

文献［10］推荐采用不平衡推力法计算边坡安全系数。不平衡推力法遵循摩尔库伦强度准则，将滑体划分为若干土条，并假定土条间作用力的合力平行于上一土条底的滑面。由于第1 块土条以上没有推力，故推力F0=0。对于其他土条，可将土条间作用力投影到底滑面上，据此可得到相应的推力Fi平衡方程为：

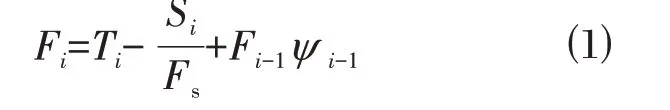
式中：ψ i-1、Si及Ti的表达式为：

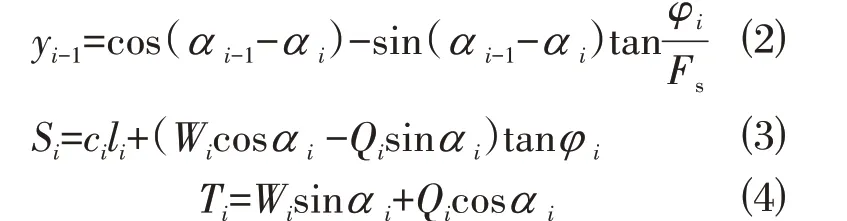
式中：i代表土条编号；Wi为各土条的自重；Qi为水平力；α i为土条各分条底边与水平线的夹角；ci为黏聚力；tanφ i为摩擦系数；li为各土条底边长；ui为底部孔隙水压力；Fi为不平衡推力；Fs为边坡安全系数；ψ i-1为第i-1 块段的剩余下滑动力传递至第i块段时的传递系数。

Alyn Wallace曾经研修天文学、工程学与物理学，现在是一位全职天文摄影师，他在家附近的威尔士及其他地区开办摄影讲习班。

隐式安全系数的计算需要用到迭代法。先假定一个用于迭代的初安全系数Fs，从坡体顶部第1 块土条算起，求出其下滑力F1；再计算第2块土条在原有荷载和F1作用下的不平衡下滑力F2，其表达式如下：

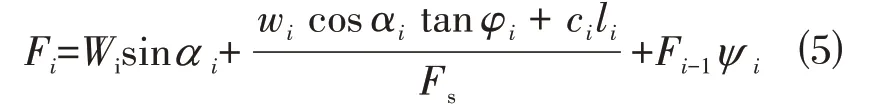
ψ i的表达式为：

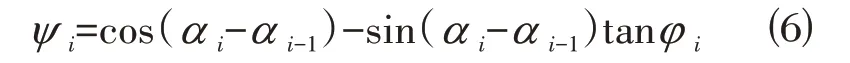
据此计算到第n块，如果该块土条在原有荷载及推力Fn-1作用下，求得的推力Fn=0，则所得Fs即为所求的坡体安全系数，否则调整Fs，依次迭代递推求解。

1.2 考虑锚杆支护的边坡稳定性分析

锚杆是目前比较经济有效的加固措施之一。当锚杆长度超过滑动面而深入坡体后，可以增强边坡潜在滑移面上的黏聚力和内摩擦角，为边坡潜在滑动体提供足够的抗滑能力，从而达到有效地阻止坡体位移，提高边坡土体强度和稳定性的目的。对于锚杆支护后的边坡稳定性，仍可采用不平衡推力法进行滑动体受力分析。

⑴锚固结构对抗滑力的作用可表达为：

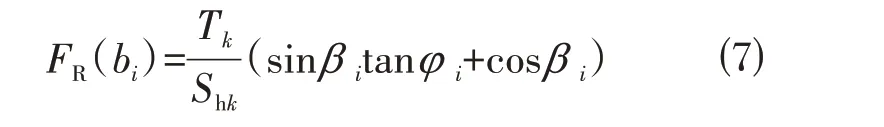
式中：Tk为第k排锚杆锚固段最大抗力；Shk为第k排锚杆水平间距；β i为第k根锚固体与滑动面圆弧切线夹角；φ i为土条i的内摩擦角。

⑵边坡安全系数Fs为：

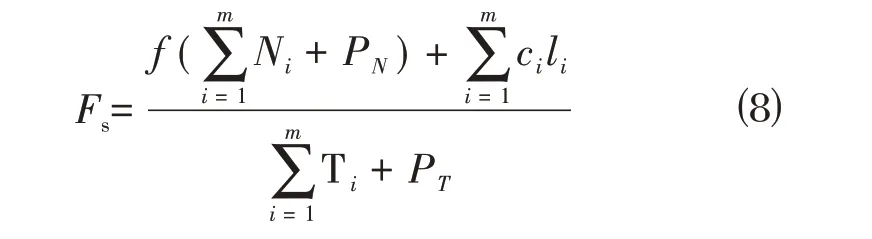
式中：Ni为作用在第i条滑面上的法向力；Ti为作用在第i条滑面上的切向力；Ci为土条第i条滑面上的黏聚力；li为第i条滑面上的长度；PN为锚杆锚固力沿滑面法向的分力；PT为锚杆锚固力沿滑面切向的分力；ƒ为滑面上摩擦系数；其他参数同上。

2 某路堑高边坡稳定性分析

2.1 工程概况

某公路高边坡位于广州市市内，全长2.65 km，道路采用1级城市主干道标准，双向四车道，设计速度为60 km∕h。该路段沿线为剥蚀丘陵地区，地势有一定起伏，植被较发育，地表孤石较多。本路堑高边坡位于K1+880～K2+015 段的路线前进的右方，坡体底边长92.2 m，纵向高为44.3 m。该段边坡共分四级，第一级坡高约6.0 m，平台宽约2.5 m；第二级坡高约10.5 m；第三级坡高约3.0 m；前三级坡坡率均为1∶1；第四级坡高1.5 m，坡率约为1∶1.25。该段边坡土体由上至下主要为砂质黏土、全风化、强风化及微风化土体。采用放坡开挖的方式对路基进行拓宽，最大挖高为37.6 m。通过现场勘察分析可得出，滑动面位于强风化和微风化交界面处，边坡的破坏模式为开挖引起沿强风化和微风化的土体交界面滑动。

2.2 模型建立

选取该公路K1+880～K2+015路堑高边坡的横断面，如图1所示，边坡岩土材料参数如表1所示。

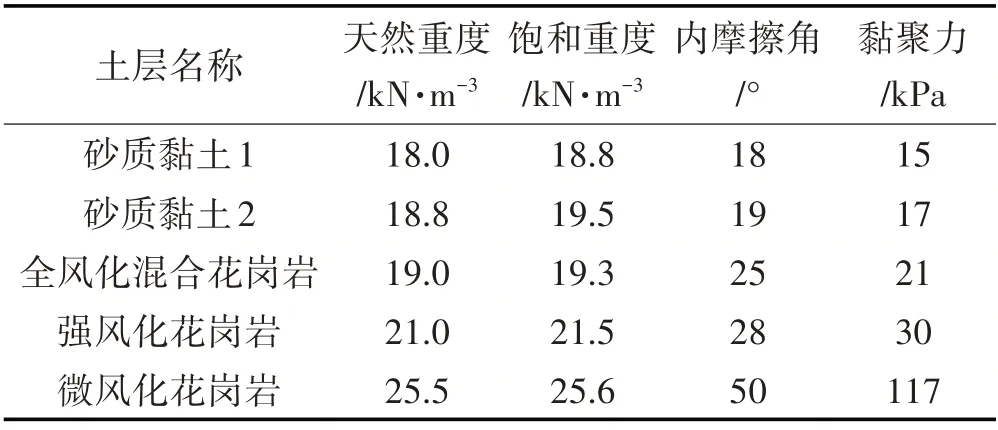
表1 边坡岩土层分布及材料参数Tab.1 Distribution and material Parameters of Slope

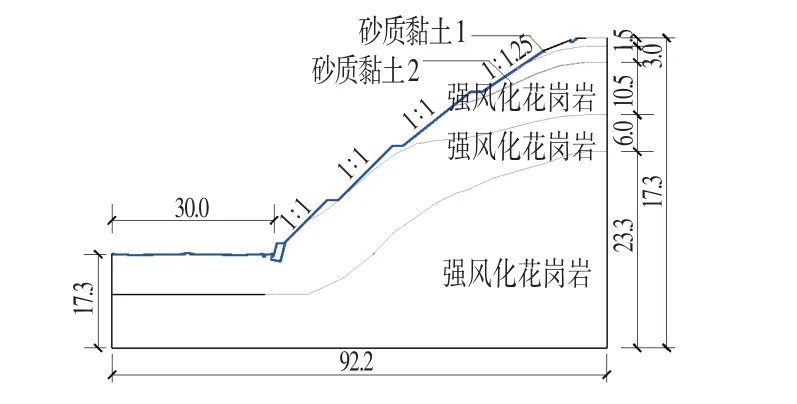
图1 边坡横断面Fig.1 Cross Section of the Slope （m）

2.3 边坡稳定性分析

根据前述理论和文献［10］，采用简布法、瑞典条分法和不平衡推力法，对自然工况、暴雨工况和地震工况下路堑高边坡的稳定性进行分析，计算结果如表2所示。

从表2 可以看出，3 种工况下该路堑高边坡的稳定性均不满足现行规范要求。因此，需要采取合理的防护加固措施，以确保边坡的安全稳定性。针对该路堑高边坡，拟采用锚杆框架梁进行支护加固，锚杆采用25 mm HRB335 钢筋制作，框架梁采用C30 钢筋混凝土进行浇筑。

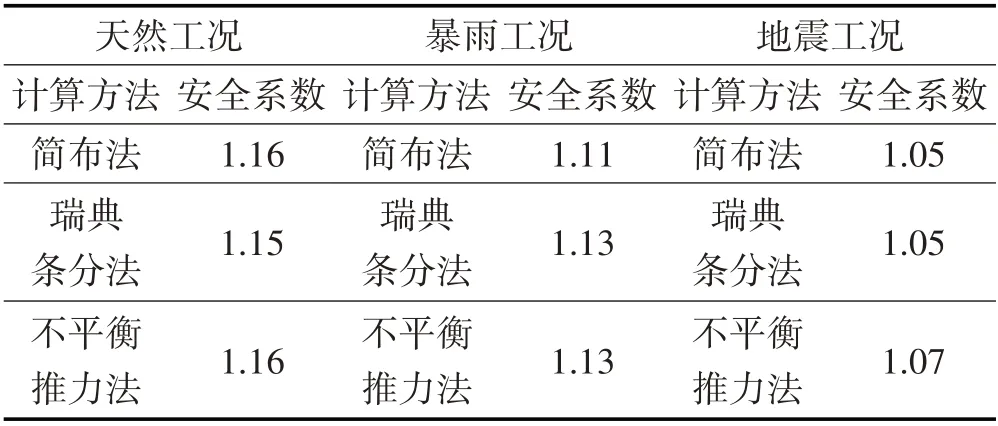
表2 不同工况下未锚固路堑边坡安全系数Tab.2 Safety Factor of Slope under Different Conditions

3 锚杆支护路堑边坡的影响因素分析

为获得更为优化合理的加固方法，针对锚杆支护路堑高边坡中的锚杆长度、水平间距以及倾角，进行相应的影响因数分析。

3.1 锚杆长度l对边坡稳定性的影响

为分析锚杆长度l对路堑高边坡整体稳定性的影响规律，取锚杆与水平面的夹角为25°，锚杆竖向和水平的间距均为3.0 m，锚固端长度均为3.0 m。各级边坡中锚杆自由长度分别为3.0 m、4.0 m、5.0 m、6.0 m和7.0 m。通过计算得到锚杆自由段长度与各级边坡安全系数的关系曲线，如图2所示。

由图2 可知，锚杆自由段长度对各级边坡的安全系数的影响比较明显。当锚杆自由段长度从3.0 m 增加至4.0 m 时，第一、二级边坡的安全系数提高幅度较小，而第三级边坡的安全系数提高较大，此时锚杆自由段长度增加对边坡整体锚固效果影响不大。但是，当锚杆自由段长度由4.0 m 增至7.0 m 时，边坡安全系数随锚杆长度增加而急剧提高，边坡整体安全系数约由1.60 提高至1.87，即锚杆自由段长度每提高1.0 m，其整体安全系数约提高0.09。这是因为当锚杆长度增加至超出潜在滑动面时，继续增加锚杆的长度，对边坡整体稳定性的提高已不明显，这就是所谓的有效锚固长度效应。另外，由上述分析可知当锚杆自由段长度大于3.0 m，即锚杆总长大于6.0 m 时，边坡整体安全系数均满足Fs＞1.35的设计要求［10，15-16］。

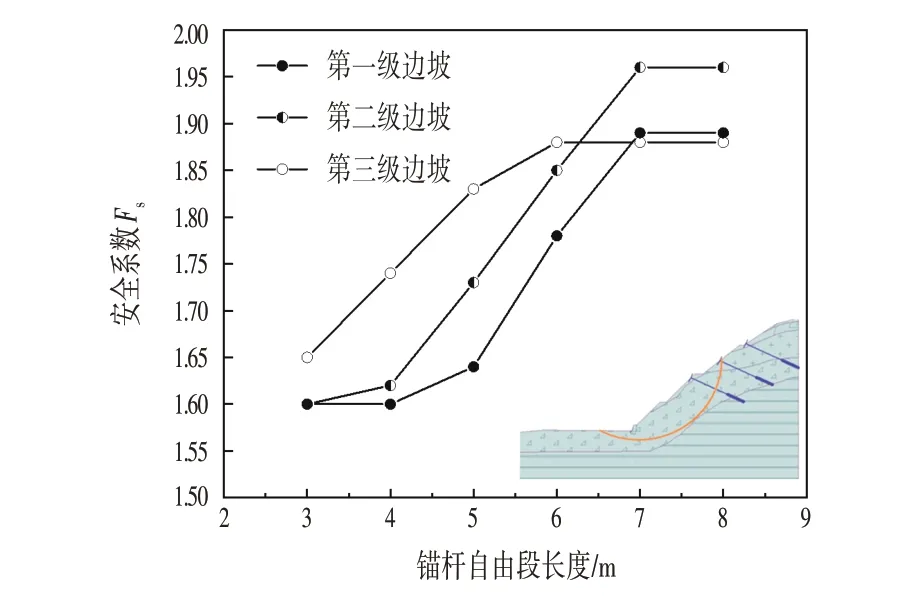
图2 锚杆自由段长度与边坡安全系数关系曲线Fig.2 Relationship Curve between Bolt Length and Safety Factor of Slope

3.2 锚杆水平间距h对边坡稳定性的影响

为分析不同水平间距下锚杆支护路堑高边坡整体稳定性的影响，现选取锚杆与水平面的夹角为25°、锚固端长度3.0 m、锚杆总长度6.0 m、锚杆竖向间距3.0 m 等设计参数不变，计算锚杆水平间距h分别为2.0 m、2.5 m、3.0 m、3.5 m 及4.0 m 下，路堑高边坡的安全系数；所得锚杆间距与各级边坡安全系数的关系曲线如图3所示。

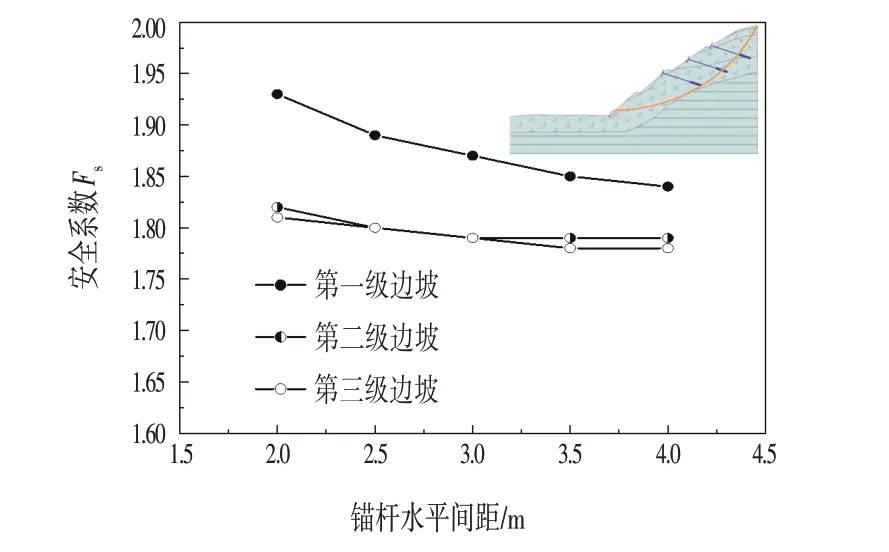
图3 锚杆水平间距与边坡安全系数的关系曲线Fig.3 Relationship Curve between Horizontal Bolt Spacing and Safety Factor of Slope

由图3 可知，路堑高边坡的整体安全系数随锚杆水平间距的增加而逐步降低。当锚杆水平间距从2.0 m增至4.0 m 时，第一、二、三级坡的安全系数分别降低了0.12、0.03 和0.02。其中，第一级坡的降低速率最大，约为4.7%。相对来说，锚杆水平间距对第二、三级坡安全系数影响较小，对第一级坡的影响较大。但是当锚杆水平间距在2.0～4.0 m 内，该路堑高边坡的整体稳定性均大于1.35，说明在该范围内取值均满足设计要求。但是考虑到经济性，该路堑高边坡的锚杆水平间距均可取3.0 m。

3.3 锚杆倾角α 对边坡整体稳定性的影响分析

为分析锚杆倾角对路堑高边坡稳定性的影响，保持锚杆锚固端长度3.0 m、锚杆自由端长度3.0 m、锚杆竖向和水平间距均取3.0 m 等设计参数不变，计算锚杆倾角分别为10°、15°、20°、25°和30°时，路堑高边坡的安全系数。不同锚杆倾角下的各级边坡的安全系数如图4所示。

由图4 可知，锚杆倾角对路堑高边坡稳定性的影响较大。当锚杆倾角由10°增至20°时，第一、二级坡的安全系数呈线性急剧增加，而第三级坡的安全系数则随之逐渐降低；当锚杆倾角由20°继续增至30°时，第一级坡的安全系数增加幅度较小，第二、三级坡的安全系数却随之逐渐减小。另外，当锚杆倾角在10°～30°内取值时，各级边坡的安全系数均大于1.35，说明路堑边坡的整体稳定性均满足设计要求。相对而言，取锚杆倾角为20°，对应的各级边坡的稳定性最为合理，锚固效果更优。

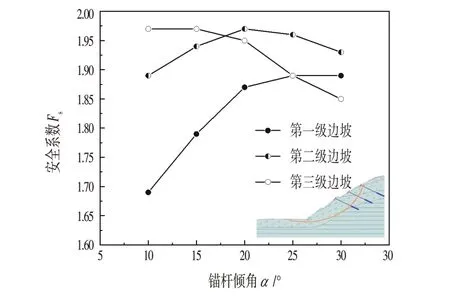
图4 锚杆倾角与边坡安全系数的关系曲线Fig.4 Relationship Curve between Bolt Inclination Angle and Safety Factor of Slope

4 结论

基于极限平衡法对不同工况下某路堑高边坡的安全稳定性进行了计算，并根据锚杆框架梁的支护方式进一步分析了锚杆长度、水平间距及锚杆倾角等设计参数对路堑高边坡稳定性的影响。本文所得结论如下：

⑴路堑高边坡加固前，3种工况下的安全系数均不满足文献［10］要求，提出了利用锚杆框架梁加固该路堑高边坡的支护方案；

⑵对于锚杆支护路堑高边坡，其整体稳定性随锚杆长度增加而提高；当锚杆长度由6.0 m增加至9.0 m时，边坡整体安全系数由1.60提高到1.85；

⑶随锚杆间距增加，边坡整体稳定性逐渐降低；当锚杆间距由2.0 m 增至4.0 m 时，边坡整体安全系数下降了4.7%；当锚杆水平间距在2.0～4.0 m 内，该路堑高边坡的整体稳定性均大于1.35，考虑到经济性，锚杆水平间距取3.0 m更为合理。

⑷随锚杆倾角的增大，边坡整体安全系数呈先增加而后保持不变的发展规律。取锚杆倾角为20°，对应的各级边坡的稳定性最为合理，锚固效果更优。

综上所述，锚杆支护该路堑高边坡的最优方案为锚杆总长度6.0 m（锚固3.0 m）、锚杆间距3.0 m、锚杆倾角20°。