基于深度学习的抽油机井工况诊断方法

肖 翔

(中国科学技术大学 信息科学技术学院，安徽 合肥230026)

0 引言

基于游梁式抽油机井的人工举升法[1]是目前主流的采油法。人工举升法以其结构简单、成本低廉、适应性强等优点著称。据不完全统计[2]，全球超过90%的油田以及国内超过85%的油田都是采用这种方式进行原油开采。在油田开采的过程中，地下深井作业的环境较为复杂，容易引起井下抽油泵从正常的状态转变为故障的状态。若抽油泵长期处于故障状态，抽油泵设备会加速磨损使其生命周期骤缩，进一步影响油田的开采效率。由实时监测的数据快速、准确地诊断识别出抽油机井的工作状态，会给实际的开采提供有价值的信息，实现高效开采的同时将损耗降至最小。

基于示功图[3]的故障诊断的方式是趋于成熟的一种诊断技术。示功图是由地面驴头悬点处的位移为横坐标，以载荷为纵坐标绘制而成的闭合曲线。泵功图则描述抽油泵处位移、载荷的曲线。虽然泵功图更能直接反映抽油泵在一次往复过程中的工作状态，然而直接测量井下的泵功图数据比较困难。因此，在实际的工程中通常使用测量比较简单的示功图代替井下泵功图。示功图具有实际的物理意义，不同工作状态的示功图在形状上存在特定的差异。从示功图的形状轮廓识别出具体的所属工况需要一定的专业知识，早期是由有经验的工程师协作完成，但是由于油井规模越来越大，采集得到的示功图数以万计，由人工来诊断十分繁琐且枯燥。若能提升计算机识别的准确率以满足生产需要，则计算机可以完全取代工人诊断。

基于示功图的计算机辅助诊断，近年来获得学者与研究人员的高度重视，诸多方法如专家系统[4]、模糊理论[5]、神经网络[6]、支持向量机[7]等先后被挖掘并应用于故障诊断任务。这些方法大多遵循先特征提取后模式分类的原则。特征提取是对原始数据降维达到降低问题的复杂度并能够保留原始数据的有效信息的技术，常用的方法有傅里叶描述子、不变矩理论、灰度矩阵特征提取[8]；模式分类是预测特征向量所属类型的技术，可以通过建立专家库计算相似度或通过机器学习算法设计分类器判别。然而，特征的选择需要借助经验和先验知识，人工特征提取的过程中存在信息丢失，直接影响后续分类器的最终性能。利用计算机出色的计算能力以及大量的历史数据的深度学习[9]，通过自动特征学习，刚好可以填补这一空缺。

受卷积神经网络(Convolutional Neural Networks，CNN)在图像处理的启发，本文提出基于卷积神经网络的示功图工况诊断模型，通过实验分析网络结构对模型性能的影响，设计出一种基于贪心策略的局部最优的卷积神经网络模型。实验结果表明，所提出的模型对未知的数据具有较强的预知能力，换言之，模型拥有优良的泛化性能。

本文提出基于CNN的功图工况诊断的方法，主要分为两个部分：离线训练与在线诊断，对于要求实时性诊断的任务，可以先离线利用历史样本将模型训练好，再对实时测量的新数据在线预测所属工况，工作流程如图1所示。

图1 示功图识别流程图

首先介绍了本文的研究背景与现状，接着简要阐述了卷积神经网络，然后对本文的数据集进行说明并阐明预处理过程，并通过实验设计结构最优的网络模型，最后对全文作出总结并提出了改进方向。

1 CNN模型

1.1 CNN结构

在早期的图像识别研究中，最大的挑战是如何组织特征，因为图像数据不像其他类型的数据那样可以通过人为理解来提取特征，需要借助SIFT、HoG等算法提取具有区分性的特征，然后利用SVM等机器学习算法识别。CNN可以直接接受原始图像作为输入，不需将特征提取与分类过程分离，其在训练时自动提取最显著的特征。

典型的CNN由输入层、卷积层、池化层、全连接层和输出层构成。本文采用一种基于LeNet[10]的CNN网络结构作为图像样本的分类器，如图2所示。输入层的大小由输入图像的分辨率决定，而输出层的大小则由分类任务的类别数确定，激活函数一般为选择为softmax，对应属于每个类别的概率。卷积层的目的则是由卷积核操作提取上一层的最基础的特征如点或边，一般称之为特征图，只要卷积核的数量足够多，就可以将每个卷积核提取的基础特征组合抽象成有效的高阶特征，整个过程中卷积核权值共享，可以降低模型的复杂度，减小计算量的同时避免出现过拟合。为避免训练过程中出现梯度弥散和梯度爆炸的现象，卷积层的激活函数通常选择为ReLU。一个卷积层后面连接一个池化层，一般采用最大池化操作降低维度，保留最显著的特征，提升模型的抗形变能力。卷积池化层的多层堆叠抽象组合出更高阶的特征，可以提升模型的表达能力。将最终提取的有效高阶特征进一步输入全连接层进行分类识别。

图2 LeNet-5结构图

1.2 性能度量

在评估模型的泛化能力时，不同的性能度量方式往往会得到不一样的衡量结果，一般由任务需求决定。本文采用正确率和错误率来评判算法性能的优劣。

假设D={(x1，y1)，(x2，y2)，…，(xm，ym)}数据集，其中xi为样本，yi为其对应的标签，模型为f。

准确率(Accuary)表示被分对的样本数量占所有样本数的比重，相应地，错误率(Error)表示分类错误的样本占样本总量的比重，计算公式为：

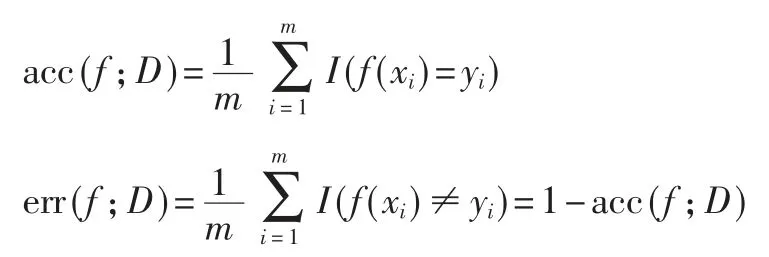
式中，I(·)表 示指示函数。

2 预处理

2.1 数据准备

本文数据源于某油田2019.01~2019.03不同油井的作业监测数据，该数据集合了不同类型传感器的采集结果，主要为电参、力参及其他参数，存储于后端服务器的数据库中。从数据库中读取无标注的原始数据，选取其中的光杆载荷和位移属性后，对数据清洗与自行标注。由于传感器每隔30 min就会测量一次光杆的载荷和位移数据，一般而言，前后测量的数据绘成功图差异不大，直接使用这些样本容易使模型对某些功图形成特殊偏好。为突出样本的多样性，采用以下策略筛选样本：

(1)保留去除重复值、异常值后的样本集合；

(2)按日期和井号分组，提取每天不同井号的首个记录、中间记录、末尾记录共三个记录；

(3)检查提取样本的完整性，若出现缺省值，轻度缺省采用平均值填充，重度缺省则丢弃。

基于上述策略，共提取出9类工况4 193份样本，将样本以8:2划分为训练集与测试集。样本分布如图3所示，详细分布见表1。

图3 样本分布图

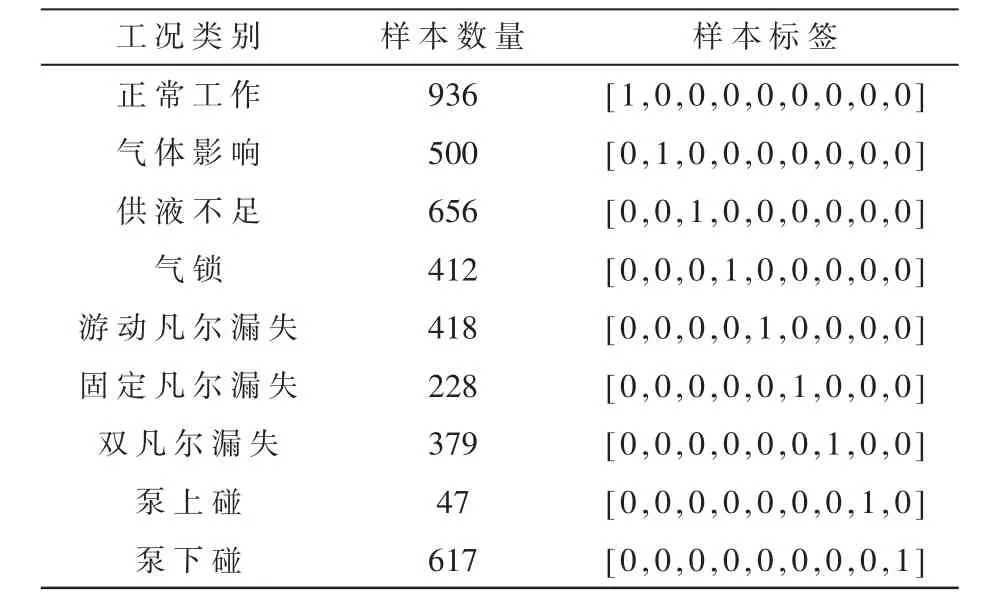
表1 数据集细分表

2.2 预处理

一般来说，样本的好坏决定最终模型分类性能的上限。对数据准备工作中获取的光杆载荷和位移向量，需要进行预处理使之满足某种协议，使处理后数据可直接作为后续模型的输入。具体步骤概括如下：

(1)正则化

将信号的数值限制在[0，1]之间，可以降低计算的复杂度加速模型收敛，同时消除不同井号量纲的影响，对不同的新数据适应性强。

(2)信号图像转化

CNN对2D图像输入数据的扩展性强，可通过2D卷积核进行卷积操作直接获取输入图像的特征图。本文采用绘图软件，将两个1D向量绘制成平面图像，再保存成64×64分辨率的像素矩阵存储在文件中，便于后续读取。

(3)图像二值化

设置像素矩阵的平均像素值为阈值，大于阈值的像素置为255，小于阈值的像素置为0。图像二值化的目的是使像素矩阵稀疏化，优化计算过程，加速模型收敛。

图像处理过程如图4～图6所示。

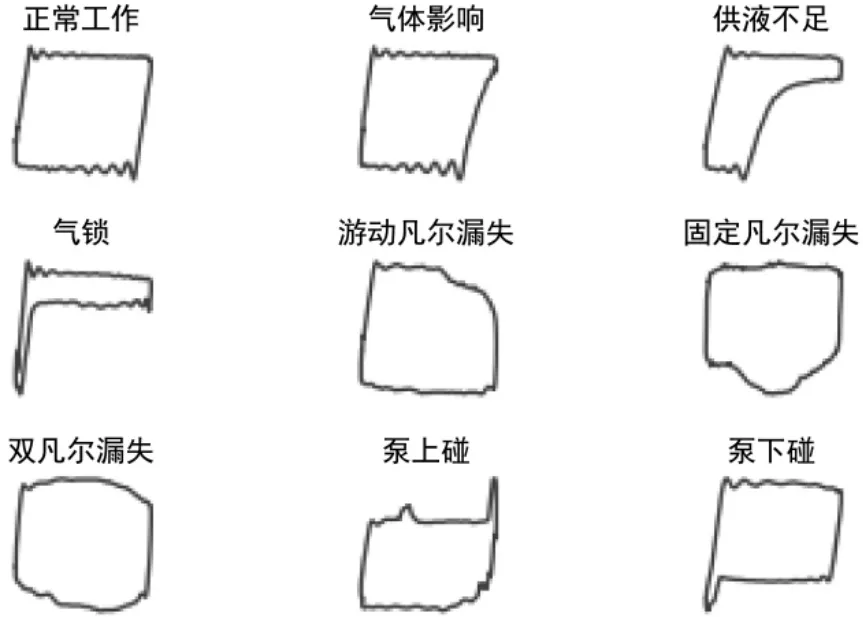
图4 原始图像

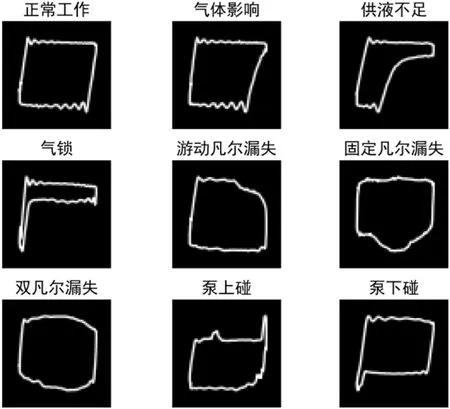
图5 灰度图像

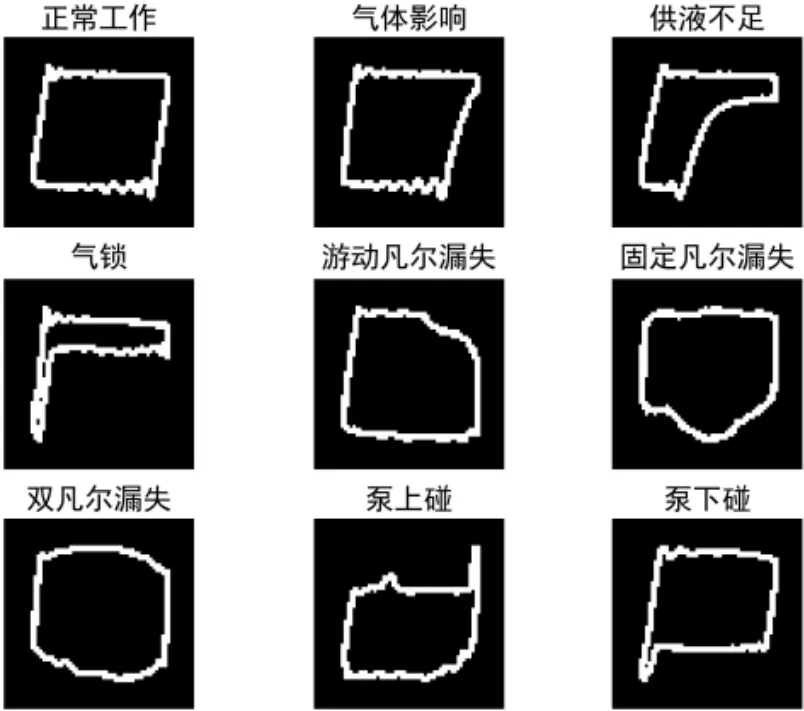
图6 二进制图像

3 实验探究

对于分类任务而言，特征选取的好坏直接决定网络最终性能的上限。因此对卷积核的探究显得格外重要。本小节采用LeNet-5框架结构，在此基础上细微改动增加一个dropout层。该网络结构为卷积层与池化层交替堆叠两次，再与全连接层交互，然后连接一个dropout层，最后通过softmax层输出。

本小节的实验框架如图7所示。

图7 探究不同卷积核对实验影响

为更好地探究卷积核对网络的影响，利用控制变量法将除卷积核外的参数设为一致：如设置随机种子，使权值伪随机初始化；预设置学习率为0.001，调用Adam优化算法更新权值加快网络收敛；池化操作选择最大值池化，大小为2×2，步长设置为2。分别将卷积核窗口尺寸设置为5×5、3×3、2×2，步长为1；第一个卷积层卷积核数量设置为8，第二个卷积层卷积核数量设置为16；全连接层由128个神经元节点构成的隐含层与9个节点构成的输出层组成。

实验过程采用交叉验证的思想，将由留出法划分的训练集样本再次拆分为训练集与验证集，具体使用10折交叉验证实现，将样本分为10份，轮询取其中1份为验证集，而剩余的9份自动变为训练集。这样拆分出10组训练集与验证集的不同组合，相应地对应10种不同的结果。分别对每组展开训练，将10组训练结果的平均值作为最终的输出，消除了随机偶然性对网络训练过程的影响，使结果更具有说服力与代表性。

3.1 卷积核为5×5

经10折交叉验证后发现，网络在大约200次迭代后逼近收敛，训练样本准确率在94.5%上下波动，而验证样本的准确率较为平滑，且与训练样本的准确率偏差不大，说明网络在训练过程中拟合程度恰好；对于网络输出的交叉熵损失值，相较于准确率训练样本与验证样本在损失函数曲线的逼近程度更高，几近重合，收敛于0.13，进一步证实了网络的拟合性能恰好，未偏向过拟合或欠拟合任意一方。

通过测试集平均值得到最终的准确率为97.7%，整个过程耗时63.03 min。训练过程如图8所示。

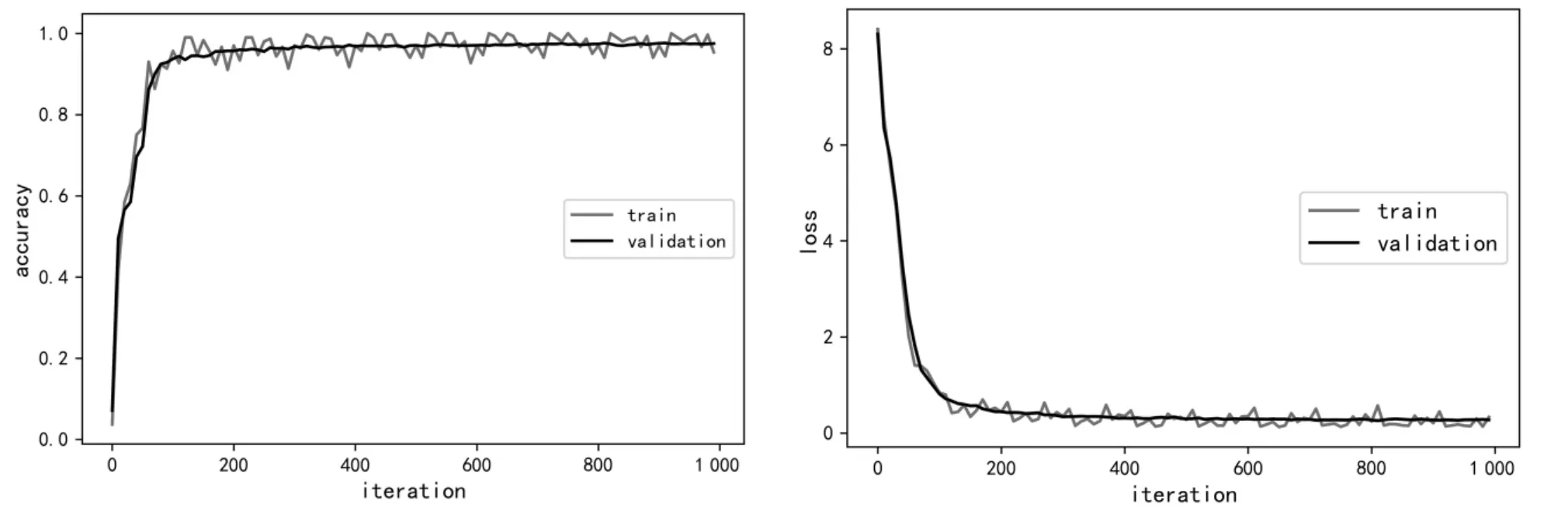
图8 卷积核为5×5的网络训练过程

3.2 卷积核为3×3

经10折交叉验证后发现，网络在大约200次迭代后逼近收敛，训练样本准确率在97.5%上下波动，波动较为明显，且验证样本的准确率也呈现一定的轻微波动，但与训练样本的准确率偏差在可控的范围内，说明网络在训练过程中稳定性稍差，拟合程度较好；对于网络输出的交叉熵损失值，相较于准确率训练样本与验证样本在损失函数曲线的更为贴近，偏差稍小，最终收敛于0.07，在性能方面与5×5相比较而言优越，从准确率和损失曲线来看则在稳定性与拟合程度方面差些。在满足基本要求的前提下，为追求性能，选择3×3卷积核是更好的选择。

通过测试集平均值得到最终的准确率为98.1%，整个过程耗时52.18 min。训练过程如图9所示。

图9 卷积核为3×3的网络训练过程

3.3 卷积核为2×2

经10折交叉验证后发现，网络在大约200次迭代后逼近收敛，训练样本准确率在96.6%上下波动，波动较为剧烈，说明样本在训练过程中极不稳定，但验证样本的准确率相对比较平滑，导致训练样本的准确率与验证样本的准确率偏差在可控范围内。方差较大，说明网络在训练过程中拟合程度稍差，容易出现拟合不足的现象。该现象同样体现在损失曲线上，对于网络输出的交叉熵损失值，训练样本损失在0.09上下浮动，较为频繁，但验证样本的损失相对比较平滑。在性能方面，相较于5×5而言略微占优，从准确率和损失曲线来看则在稳定性与拟合程度方面明显差距，导致一般情况下，极少直接使用2×2卷积核。

在测试集平均值得到最终的准确率为97.8%，整个过程耗时47.32 min。训练过程如图10所示。

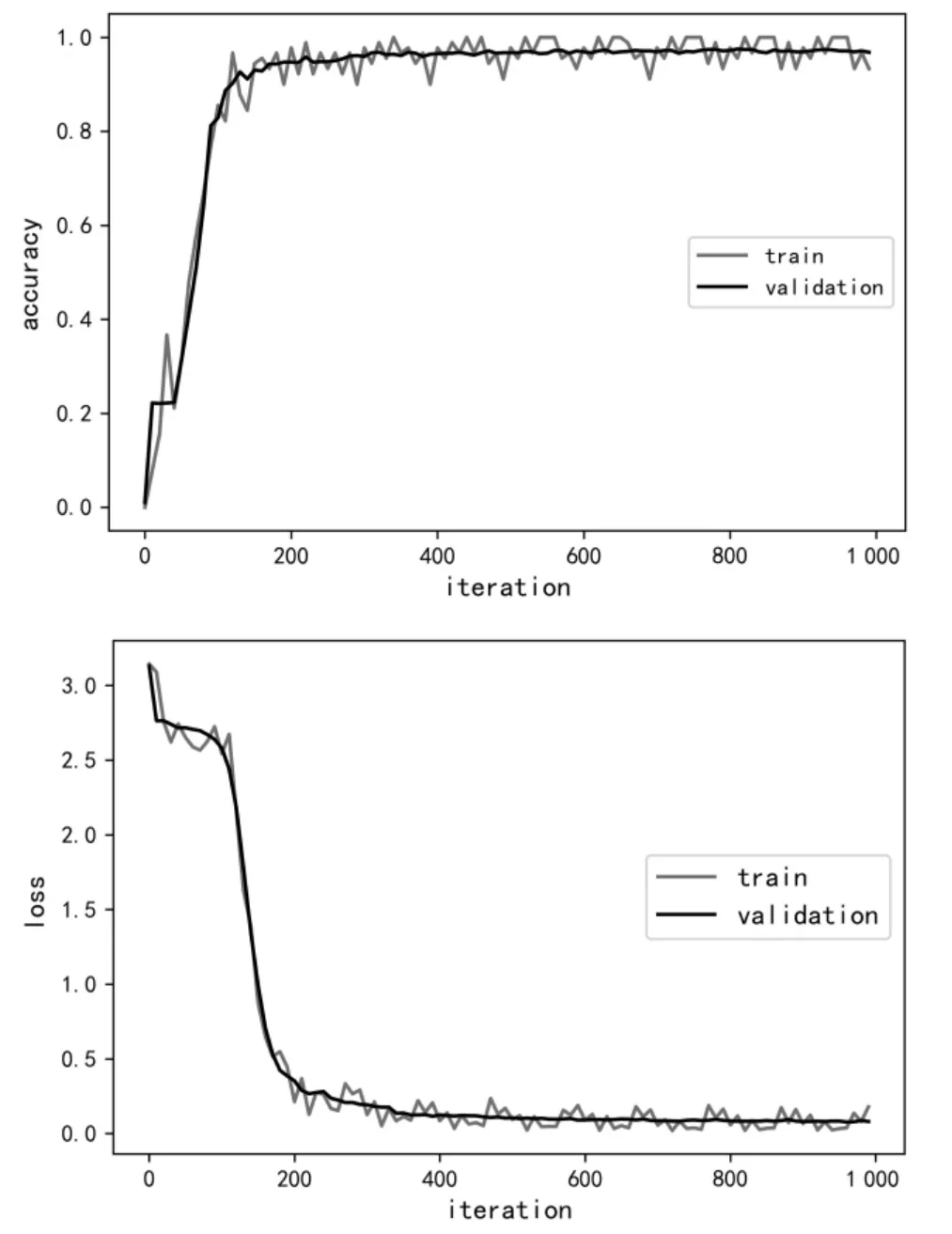
图10 卷积核为2×2的网络训练过程

4 实验总结与改进空间

利用已有数据，在文献[11]提出的目前先进的自编码机算法作出一组对照实验，具体数值见表2。

由表2可以看出，卷积核大小直接影响网络最终的性能。在上述CNN三个实验中，网络均处于正常拟合状态，性能都达到指标要求，过程也都近似，譬如都通过大约200次迭代逼近收敛，收敛的过程中训练准确率与验证准确率偏差不大，训练损失与验证损失偏差也不大，较自编码机500次迭代收敛效率更高。而差异更多体现在最终的性能指标上，如5×5卷积核的训练准确率在94.5%左右，3×3卷积核为97.5%左右，2×2卷积核为96.6%左右，在表现上3×3积核最优，5×5卷积核较差，但仍比自编码机性能好。该结论也同样适用于各卷积核中训练样本损失值。不失一般性，测试集准确率同样遵循这一结论，5×5卷积核平均测试准确性只有97.7%，CNN中三者最低，较于自编码机泛化性能好得多。在时间复杂度上，与卷积核大小呈现正相关，具体体现在计算的复杂性上，由模型的规模决定，而自编码机实验计算却复杂得多。

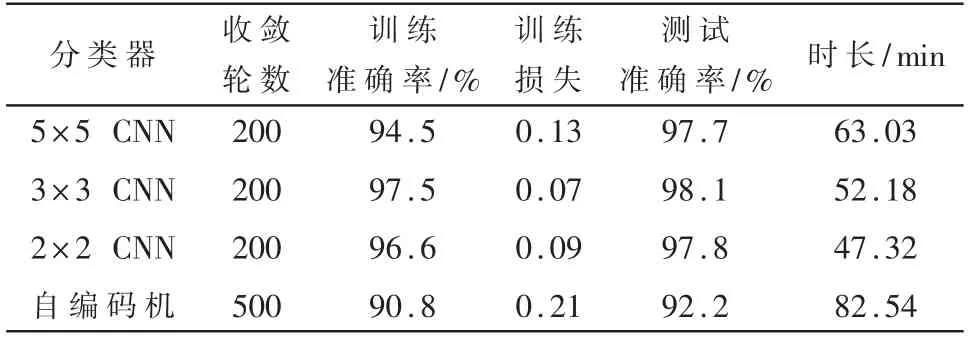
表2 不同结构分类器性能对比

实验结果表明，3×3卷积核实验中表现最佳，预测准确率高达98%，验证了本方法的有效性与可行性。

显然，由于本文主要针对有限、无标注的数据进行学习训练，预测的准确度受输入标签和算法的共同影响。若想要进一步提升模型的准确率，可以从两个方面进行扩展：(1)为尽量减少人为标注带来的误差，一方面通过挑选一部分有充分理由证明是正确的标签样本为训练集，但训练集的数量必然不会多，另一方面对海量无标签的数据进行半监督学习，设置阈值通过轮询学习使得更多的样本加入到训练集中，迭代一定次数获得的训练集比人为模糊性标注的样本更具有说服性；(2)改进模型算法，对于数据多、分辨率大的图像数据，可以换用AlexNet[12]、VGG-16[13]甚至更复杂的ResNet[14]网络解决。