分辨矩阵在逻辑优化中的应用

闫心怡，温 馨，陈泽华+

1.太原理工大学 电气与动力工程学院，太原 030024

2.太原理工大学 大数据学院，太原 030024

组合逻辑电路[1]由门电路组成，门之间的相互连接形成了逻辑网络。逻辑网络可由布尔函数或真值表来描述。通过化简布尔函数或真值表，可以减少逻辑网络的复杂性，从而提高电路的可靠性并降低系统功耗。K-map（Karnaugh map）[1]是典型的图形表示的布尔函数化简方法，当输入变量超过5 时其图形难以理解。Q-M（Quine-McCluskey algorithms）[1]方法更便于计算机计算，但是Q-M 算法的运行时间随变量数量呈指数增长。随着电路规模不断扩大，数据挖掘理论的迅速发展，从知识工程角度重新考虑逻辑电路优化，是一种新的思路。

经典粗糙集理论由Pawlak 提出，除了通过定义上、下近似完成知识的近似表达，还可以基于等价关系处理信息系统，在保证信息不减的前提下实现知识约简或规则提取。

Skowron 教授提出的不可分辨矩阵[2-3]是信息系统属性约简和规则提取的经典方法，在此基础上衍生出很多相关改进算法[4-11]，有学者将其与覆盖[6]、模糊粗糙集[7]启发式算子联系起来构建新的辨识矩阵，使之能够对一致、不一致系统进行更为有效的属性约简和规则提取。近年来，学者将分辨矩阵和形式概念分析[12-14]结合起来，基于分辨矩阵的方法也在形式概念分析中发展起来。

在逻辑电路的分析与设计中，真值表用来表征数字逻辑电路输入与输出之间的逻辑关系，真值表约简是逻辑优化的理论基础。本文将真值表看作逻辑信息系统（logic information system，LIS）[15]，在传统分辨矩阵基础上构造了粒分辨矩阵，与多粒度形式概念分析的类属性块方法[16]中一样，试图寻找决策蕴含与不同属性组合之间的关系，但是不同的是本文通过定义信息粒来分析属性与决策间的关系，将逻辑电路化简转化为基于粒分辨矩阵的LIS 最简规则发现问题。该方法避免了传统分辨矩阵中大量的矩阵元素计算问题，同时证明了该方法与传统卡诺图约简的等价性。

1 预备知识

数字电路可以用布尔函数以及真值表进行表示。它们处理的是“0”“1”信号。

定义1（真值表）真值表是表征逻辑事件输入和输出之间全部可能状态的表格，它对所有可能的逻辑输入定义了对应的逻辑输出，用逻辑关系的表格形式表示。真值表的输入包括了全部n个变量的乘积项（每个变量只以原变量或反变量的形式出现一次），称为最小项。n个输入变量的真值表包含2n个最小项，用表示。

定义2（最小项表达式）真值表中对应所有逻辑函数值为1 的最小项之和，称为最小项表达式。

定义3（最简逻辑函数表达）化简后的真值表中所有逻辑函数值为1 的条件属性乘积项的组合称为最简逻辑函数表达式。

定义4[15]（逻辑信息系统）定义LIS=(U,R,V,f)为一个逻辑信息系统，其中U为论域，|U|表示论域元素个数，R=A⋃Y为属性集，A={A1,A2,…,Am}表示逻辑信息系统的输入变量（条件属性），|A|表示条件属性的个数，Y={Y1,Y2,…,Yn}表示逻辑信息系统的输出变量（决策属性），|Y|表示决策属性的个数。V={0,1} 是属性值的值域，f:U×R→V是一个信息函数，它指定U中每一个对象的属性值。

真值表是一个逻辑信息系统，它的每一行代表一条逻辑规则。

特殊地，当n=1 时，这是一个多输入单输出逻辑信息系统。

从逻辑信息系统的角度研究真值表，可以将数字逻辑电路中的逻辑优化问题转化为信息系统最简单规则发现问题。

定义5（信息粒）逻辑信息系统中的任意逻辑输入变量Ai∈A可以导出论域U的一个划分：

式中，fAi(u)=0 表示在属性Ai论域下具有属性值0 的论域元素u。同样的表示在属性Ai下论域中具有属性值1 的论域元素u。可以得到由输入变量Ai推导出的等价类划分，本文将该等价类划分定义为信息粒。由逻辑输入属性Ai∈A推导出的所有信息粒构成了一个信息粒集（information granular set，IGS）。

定义6（决策类划分）对于任何逻辑输出属性Yi，其属性值也将在整个论域中划分。定义U0=，表示输出属性Yi中所有属性值为“0”的论域元素。相应地，，表示输出属性Yi中所有属性值为“1”的论域元素。

显然地，U0⋃U1=U，U0⋂U1=∅。

定义7（粒分辨矩阵）本文利用等价类定义信息粒，进而构成粒分辨矩阵。对于多输入单输出信息系统，定义粒分辨矩阵：

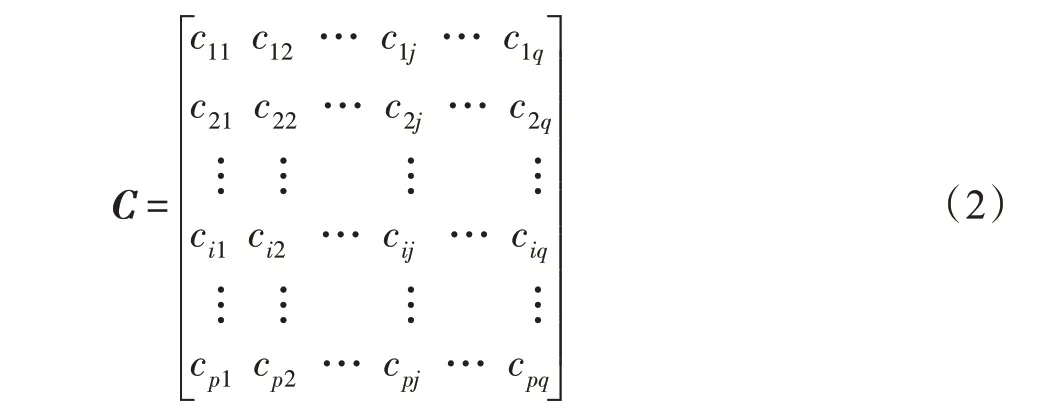
式中元素：

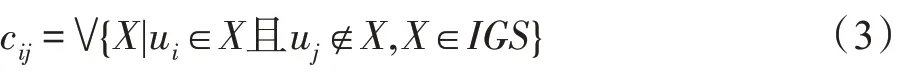
式中，cij表示信息粒集合中能够区分元素ui∈U1与元素uj∈U0的信息粒，X表示信息粒集合中的任一元素。同时p=|U1|表示输出属性Yi中所有属性值为“1”的论域元素个数。q=|U0|表示输出属性Yi中所有属性值为“0”的论域元素个数。

定义8（决策规则）组织粒分辨矩阵中的元素cij，定义决策规则：

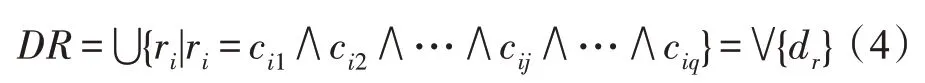
式中，ri包含所有能区分ui∈U1与uj∈U0中的所有元素，DR即为能区分等价类U0和U1的最简规则集，dr作为其中的一条规则。

定义9（启发式信息）在最简规则基础上提出启发式信息：

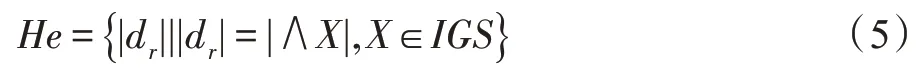
式中，|dr|表示规则的信息粒组合的个数。

2 粒分辨矩阵的逻辑表达式优化算法

根据第1 章的相关内容，本文针对真值表提出了一种基于粒分辨矩阵的约简算法。

2.1 算法描述

算法1基于粒分辨矩阵的真值表约简算法

输入：真值表。

输出：最小布尔逻辑表达式。

步骤1计算U0和U1，初始化MBE=∅，计算信息粒。

步骤2计算逻辑输出的粒分辨矩阵C。

步骤3根据粒分辨矩阵元素cij组织决策规则，计算每条规则的启发式信息He。

步骤4对He由大到小排序，判断每条规则是否存在新识别的论域元素。

步骤5若存在，将该条规则记录到MBE中；同时判断是否覆盖U1集合中的所有元素，若覆盖跳到步骤7，否则返回步骤4，继续计算下一条规则。

步骤6否则，不记录。

步骤7输出最小布尔逻辑表达式MBE，结束。

可以证明本文所提算法与K-map方法的等价性：

对一个n行真值表，设有r个最小项F输出变量值1 且Fi为其中一个最小项（0 ≤i≤r），则有n-r个最小项G输出变量值0 且Gj为其中一个最小项（0 ≤j≤n-r）。

设Fi与Gj不同的输入变量为X1,X2,…,Xs，则在卡诺图中可以形成s组互补的包围圈，其中任一组包围圈中的均包含最小项Fi在卡诺图中的“1”，而不包含Gj，因此这s组包围圈互相为“或”关系。同理，若使得Fi与n-r个输出变量值为0 的最小项G都区分出来，则需Fi与n-r个最小项形成的包围圈互相为“与”关系。

粒分辨矩阵中，行为真值表中输出为1 的最小项Fi，列为输出为0的最小项Gj。矩阵元素cij为Fi与Gj不同的逻辑输入变量，cij中任一变量均可区分Fi与Gj，故cij中，各变量为“或”关系，cij=X1∨X2∨…∨Xs，cij和Fi所在s组包围圈对应。同理，若欲得到Fi与所有输出变量值为0 的最小项G都不同的逻辑输入变量，需n-r个cij为相“与”关系，即ci1∧ci2∧…∧cir。由上述分析可知，粒分辨矩阵方法与卡诺图方法原理相同，故粒分辨矩阵方法等价于卡诺图方法。

2.2 实例说明

逻辑电路与逻辑表达式是可以转化为真值表来表示的，本文将通过例2 来说明算法1 的实施过程。

例2对于图2 逻辑电路图，其函数式为Y=。可以将图1 转化为如表1 所示真值表，对于有3 个逻辑输入的逻辑电路，其对应的真值表有8 行数据。

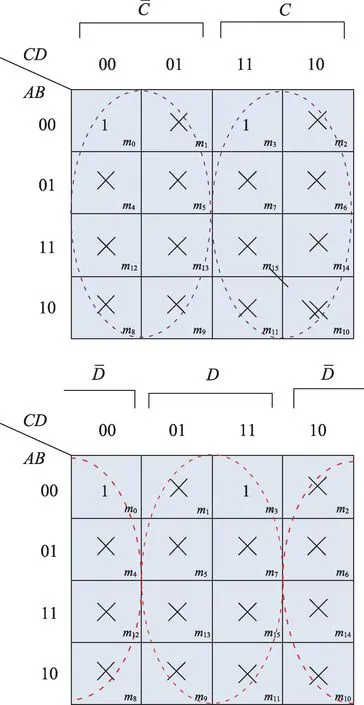
Fig.1 Complementary encirclement diagram图1 包围圈示意图

Fig.2 Logic circuit diagram图2 逻辑电路图

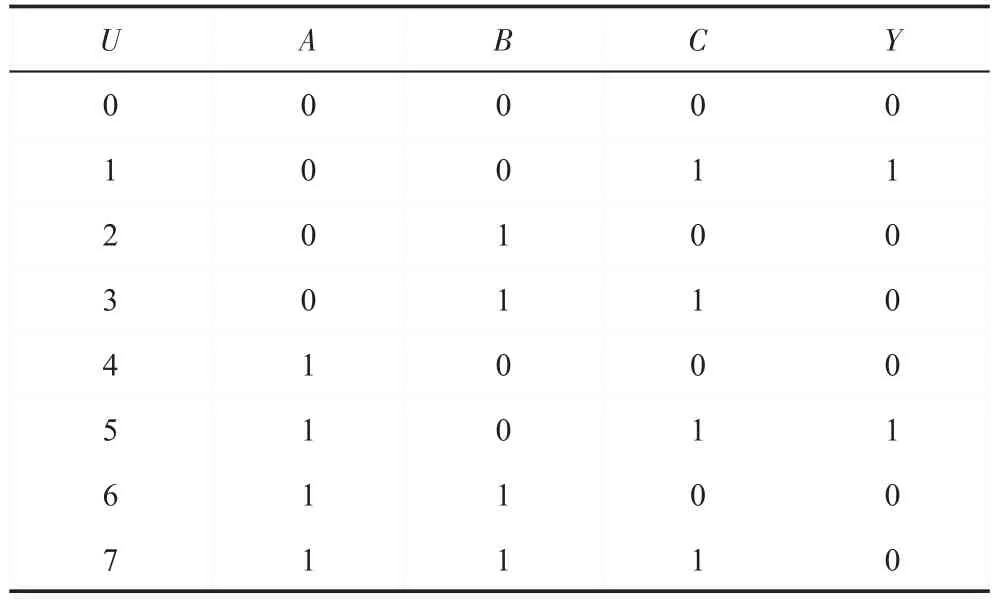
Table 1 Truth table表1 真值表

本例以逻辑输出Y为例说明本文算法的运算过程，如表1 所示，可知：

论域U={0,1,2,3,4,5,6,7}，逻辑输入属性为A={A,B,C}，逻辑输出属性为Y，根据定义4 可以得到：

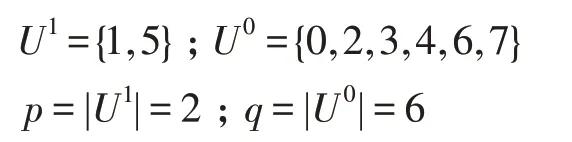
同理可得：

构造粒分辨矩阵：

同理可得矩阵中的其他元素，得到如上矩阵计算结果。

根据定义8 计算决策规则可得：

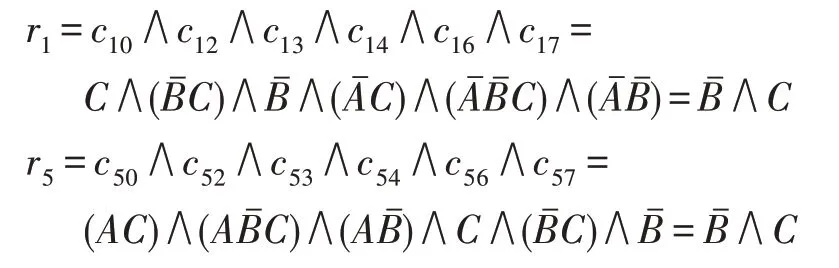
最后根据式（4）可以得到：

Table 2 Heuristic information表2 启发式信息

根据文献[1]中的卡诺图化简方法首先得到图3，由图可知卡诺图化简结果为。对比两种方法的结果可知，本文算法所得结果与卡诺图化简结果一致。

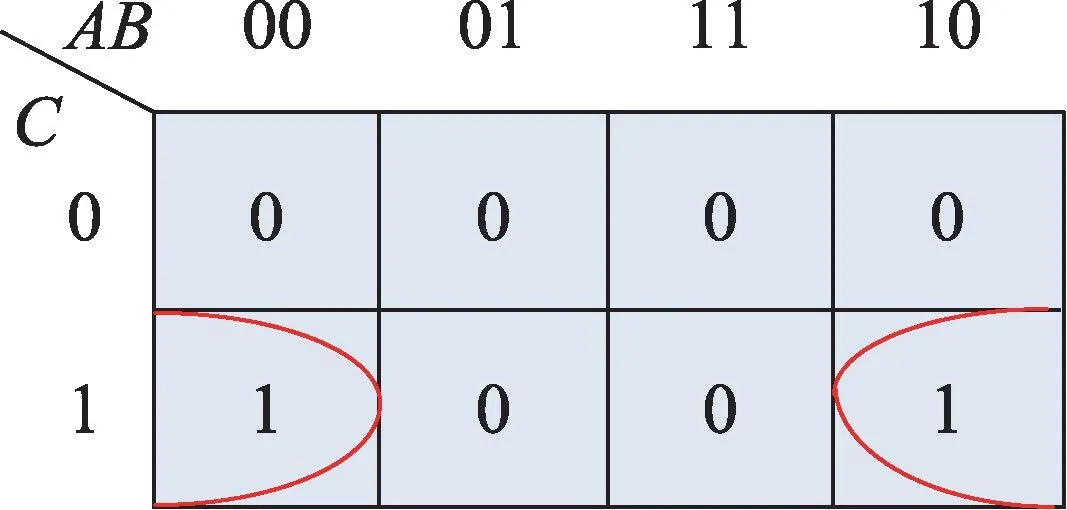
Fig.3 Karnaugh map reduction diagram图3 卡诺图化简示意图

3 算法分析

K-map 方法使用简单直观，但是图形表示难以描述5 个以上的输入变量；Q-M 算法使得K-map 方法易于在计算机上实现。对于含有m个输入的真值表，|A|=m,|U|=2m，Q-M 算法的时间复杂度为O(|U|×3|A|)，即O(2m×3m)。在粒矩阵法（granular matrix reduction algorithm，GMRA）[15]中，用粒度计算和矩阵来区分真值表中的所有“1”，将逻辑化简问题转化为布尔矩阵运算的问题，算法的时间复杂度为O(|U|2×|A|×2|A|)，即O(m×23m)。文献[17]提出的变粒度真值表约简算法（variable granularity reduction algorithm，VGRA），随着真值表的输入逻辑变量的粒度变化，通过引入标记矩阵和启发式算子，对大规模真值表进行知识约简，其算法复杂度为O(|U|×|A|×2|A|)，即O(m×22m)。文献[18]将MIMO（multiple input multiple output）真值表转化为决策形式背景，将真值表的约简问题转化为决策形式背景的最简规则提取过程，提出一种基于FCA（formal concept analysis）的MIMO 真值表并行约简算法，其算法的复杂度为O(|U|×|A|)+O(|U|2×|A|2lb(|U|×|A|))，即O(m×2m)+O(22m×m3×lbm)。

本文算法中，粒分辨矩阵C=[cij]的规模为p×q，其中p+q=2m，而经典分辨矩阵的规模为2m×2m。从矩阵的规模可以看到，矩阵复杂度大大下降。生成本文提出的粒分辨矩阵C的计算复杂度O(p×q)，决策规则的计算复杂度为O(q)，规则提取过程的计算复杂度为O(p)，故整个算法复杂度为O(p2×q2)，在最坏情况下也远小于O(22m-1)。各算法复杂度对比如表3 所示。

GMRA 算法复杂度以指数8 为底，Q-M 算法复杂度则以指数6 为底，VGRA 算法复杂度以指数4 为底。本文提出的GMD 算法，在传统分辨矩阵的基础上，简化了矩阵的规模，避免了大量矩阵元素的计算，同时利用启发因子的优势，加快算法收敛速度。较Q-M 算法以及其他算法在计算复杂度上具有明显的优势。

Table 3 Complexity comparison表3 复杂度对比

4 结束语

本文将分辨矩阵应用到逻辑优化中，提出了一种获取最小布尔表达式的方法。构造粒分辨矩阵区分真值表中的所有“1”，本文从理论证明和实例分析的角度，说明了算法的正确性和有效性。

本文的创新之处在于：（1）粒分辨矩阵与传统的分辨矩阵不同，它既不是方阵也不对称，大大减少了矩阵规模。（2）矩阵的元素由信息粒度（等价类代替属性）表示，而非将属性作为基本元素。（3）证明了本文算法与卡诺图法的等价性。（4）以覆盖真值表中所有的输出“1”为终止条件，简便运算同时避免了规则的冗余。

在下一步的研究工作中，可以继续将该方法扩展到多输出逻辑信息系统中。虽然从算法复杂度的角度来看，本文算法比以往算法的复杂度有所下降，但是依旧以指数形式增长。在以后的工作中可以探索并行计算方式，并能够将相关成果和概念研究融合起来。另外本文方法还暂未推广至普通的信息系统中，方法仍需要继续改进扩展，这也是未来努力需要解决的问题。