面积法解二面角高考题
2021-01-12 10:08:34叶文明叶丽英
数理化解题研究 2020年34期
叶文明 叶丽英
(浙江省松阳二中 323406)

一、原理

图1

二、应用举例
例1(2018年高考天津卷)
如图:AD∥BC,AD=2BC,AD⊥CD,EG∥AD,EG=AD,CD∥FG,CD=2FG,DG⊥面ABCD,DA=DC=DG=2.
(1)若M、N分别为CF、EG的中点,求证:MN∥面CDE;
(2)求二面角E-BC-F的正弦值;
(3)若点P在线段DG上,且BP与面ADGE所成的角为60°,求线段DP的长.

由已知可得BC⊥面GDCF,于是△OBC和△FBC都是Rt△.

图2



图3

(1)证明:平面AMD⊥平面BMC;
(2)当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.



图4
例3(2018年高考北京卷)

(1)求证:AC⊥面BEF;(2)求二面角B-CD-C1的余弦值;(3)证明:直线FG与平面BCD相交.
解析(1)(3)略.
(2)由已知二面角B-CD-C1与二面角B-CD-A互补,又BE⊥面ACC1A1,
∴△BCD在面ACC1A1的射影为△ECD.
∴二面角B-CD-A的平面角θ的余弦值为:

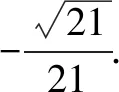
猜你喜欢
语数外学习·高中版下旬(2024年10期)2024-12-20 00:00:00
语数外学习·高中版上旬(2024年30期)2024-02-20 00:00:00
语数外学习·高中版中旬(2024年2期)2024-01-01 00:00:00
民间文学(2018年9期)2018-12-13 02:02:48
福建中学数学(2018年1期)2018-11-29 02:52:14
浙江林业(2017年8期)2017-11-13 03:31:41
绿色中国(2017年19期)2017-05-25 13:25:14
浙江林业(2015年9期)2015-12-21 01:21:10
数学教学通讯·初中版(2014年12期)2014-04-29 00:44:03
化学分析计量(2014年6期)2014-04-04 15:34:48

