小跨高比混凝土三点弯曲梁双K 断裂参数研究

尹阳阳，胡少伟

(1.河海大学土木与交通学院，南京 210024；2.重庆大学土木工程学院，重庆400045)

由于混凝土材料在施工、养护及服役期总是伴随着裂缝的存在，而作为基本的材料参数，研究混凝土断裂性能对评价裂缝的稳定性具有重要意义。据混凝土材料断裂过程的3个阶段：裂缝起裂、稳定扩展及失稳扩展，徐世烺和Reinhardt[1−3]提出了用起裂断裂韧度KIiCni和失稳断裂韧度KIuCn判断裂缝起裂及失稳扩展的双K断裂模型(DKFM)。由于其试验过程仅要求单调加载，不需要测下降段的裂缝张口位移值，从而极大地降低了对试验机刚度的要求。基于DKFM，我国于2005年推出了混凝土断裂试验规程[4]。文献[5]指出，DKFM是唯一一种被结构设计规范采用并得到广泛应用的模型。

目前大多基于跨高比为4的标准三点弯曲梁研究混凝土的双K断裂性能[4−14]。当试件尺寸较大时，自重对于跨高比为4的三点弯曲梁的断裂性能影响较大[15]。为了减小试件自重的影响及节省材料，很多学者尝试采用小跨高比三点弯曲梁研究混凝土断裂性能[16−27]。

式中：σN为三点弯曲梁试件的名义应力；a为裂缝长度；Fβ(a/h)可以认为是与跨高比和a/h有关的计算三点弯曲梁KΙC的形函数；t为试件宽度；h为试件高度；P为外荷载；W为试件跨度间自重。

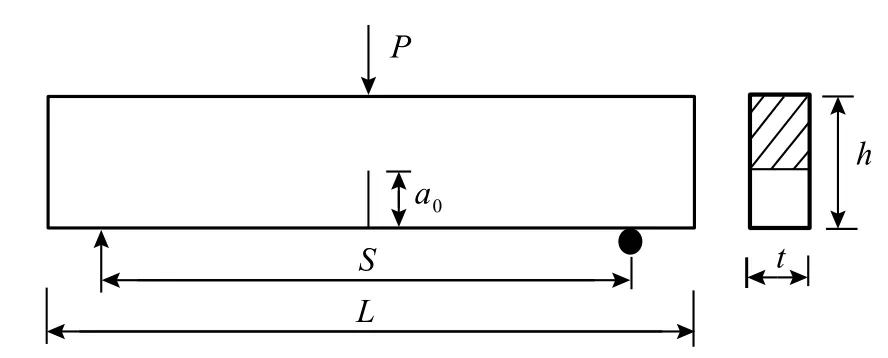
图1 三点弯曲梁试件Fig.1 TPB specimen

其中，ci为试件实测P-CMOD曲线初始裂缝张开柔度，ci=CMOD/P[4]。

将实测的CMOD代入式(3)求得a，再将a代入式(1)即可得到KΙC。

应该指出，对于采用小跨高比三点弯曲梁研究混凝土断裂性能的关键是确定试件的Fβ(a/h)及Vβ(α)。很多学者[22−27]将跨高比为4的三点弯曲梁的F4(a/h)及V4(α)应用于了研究跨高比为3和2.5的三点弯曲梁的断裂性能将使所得的双K断裂韧度偏大，从而带来不安全因素。最近，Aliha 和Mousavi[30]提出了用小跨高比三点弯曲梁研究不同材料断裂性能的概念，并基于有限元分析指出小跨高比试件可以实现纯Ι 型断裂模式。

综上可见，很有必要对基于小跨高比三点弯曲梁研究混凝土的断裂性能作进一步研究。

目前一般采用Guinea 等[31]给出的Fβ(a/h)及Vβ(α)研究小跨高比三点弯曲梁的断裂韧度[13−15]。但随着断裂力学理论应用领域的增多，并为了进一步验证文献[31]中计算公式对双K断裂参数的适用性，本文通过对跨高比为4和2.5的三点弯曲梁Fβ(a/h)及Vβ(α)的线性插值，给出了计算小跨高比三点弯曲梁断裂参数的公式，并通过开展3种小跨高比三点弯曲梁试验对两种方法计算结果进行了对比分析。最后，通过文献中已有数据进一步验证了本文所给公式的适用性。

1 双K 断裂参数计算

为了叙述的完整性，本文分别就基于线性插值法及Guinea 等[31]的方法计算如图1所示的三点弯曲梁双K断裂参数的过程简述如下。

1.1 基于线性插值理论确定双K 断裂参数

1.2 基于Guinea 等[31]的方法确定双K 断裂参数

至此，同上述基于线性插值方法计算双K断裂参数过程，即可得到基于Guinea 等[31]的方法确定的双K断裂参数。

1.3 解析法确定起裂断裂韧度

式中，fc为立方体抗压强度，由边长为150 mm 的立方体试件测得。

2 试验概况

为了验证本文所给出的公式的适用性，设计了3种跨高比试件，其中，所有试件长度L=500 mm，跨度S=400 mm，厚度t=100 mm，高度h分别为100 mm、150 mm 及200 mm，对应的初始裂缝长度a0分别为30 mm、50 mm 及60 mm。试验用混凝土由饮用水，P∙O42.5级水泥，最大骨料粒径10 mm 的石灰岩碎石，天然河砂，配合比为水∶水泥∶砂∶石子=1∶0.47∶1.369∶2.780制成。所有试件24 h 后拆模，试件拆模后均用潮湿的土工布覆盖，并在室温下养护28 d。试件试验龄期为120 d。试验前2 d，试件的预制缝由锯片厚度为3 mm 的切割机制作而成。混凝土标准立方块120 d 龄期抗压强度为47.96 MPa。

所有试验均在最大量程200 kN的万能试验机上开展，加载速率由跨中挠度控制，所有试件均为0.05 mm/min。CMOD及CTOD均由量程为2 mm的夹式引伸仪测量。试验过程中所有数据由动态应变测试系统进行采集。加载装置如图2所示。

3 试验结果与分析

3.1 P-CMOD曲线

图3给出了测得的P-CMOD曲线。可见，小跨高比三点弯曲梁的断裂过程同样可分为3 个阶段，即初始加载的线性段至荷载达到Pini时试件起裂，而后由于微裂缝的发展而进入稳定扩展的非线性段至荷载达到Pmax，当荷载达到Pmax后由于裂缝的进一步发展连通，试件进入失稳扩展阶段直至宏观裂缝出现，试件破坏[5,8]。应该指出，对于高度为200 mm 的个别试件由于峰值荷载较大，导致积蓄的应变能过大而出现了软化段荷载的突然降低。由P-CMOD曲线确定的起裂荷载Pini、最大荷载Pmax及临界裂缝张口位移CMODc及实测的临界裂尖张口位移CTODc如表1所示。随着试件高度从100 mm 增大至200 mm，Pini、Pmax及CMODc均逐渐增大，其中，Pini从2.596 kN 逐渐增大至8.576 kN，Pmax从4.533 kN逐渐增大至16.773 kN，而CMODc则从0.0378 mm 逐渐增大至0.0595 mm，分别增大了230.3%、270.0%及57.4%。

图2 加载装置Fig.2 Test device

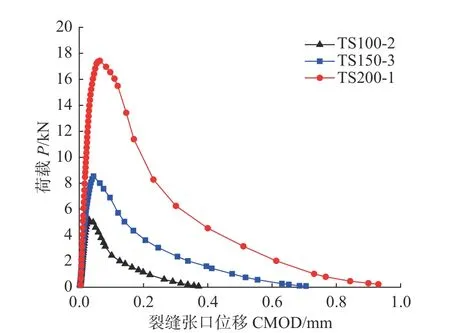
图3 P-CMOD曲线Fig.3 P-CMOD curves

破坏后的试件如图4所示，可见，小跨高比三点弯曲梁试件的裂缝扩展路径基本保持直线扩展，符合Ι型断裂模式，与文献[30]结论相同。

3.2 基于线性插值法的断裂参数

由线性插值法计算所得的计算弹性模量E、有效裂缝长度ac及双K断裂参数如表1所示。

图5给出了临界有效裂缝扩展长度(ac−a0)随试件高度的变化，可知，(ac−a0)随试件高度逐渐增大，从7.712 mm 逐渐增大至12.522 mm，分析原因是随试件高度的增大，韧带长度逐渐增大，试件的边界效应对裂缝扩展的影响逐渐减小，即试件韧带长度较大时，更利于裂缝的扩展[9]。

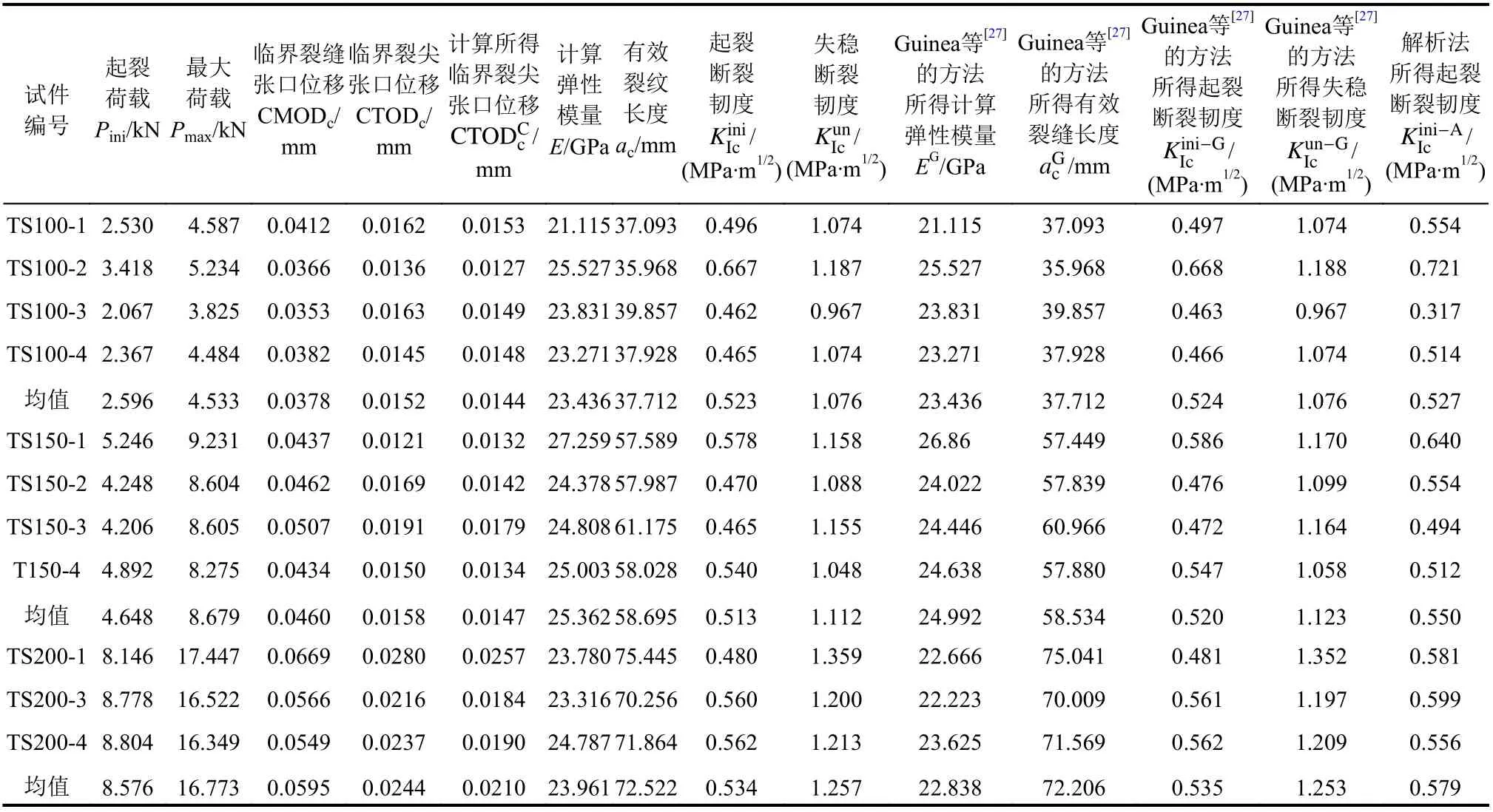
表1 试验及计算结果Table 1 Experimental and calculated results

图4 裂缝扩展路径Fig.4 Crack propagation path

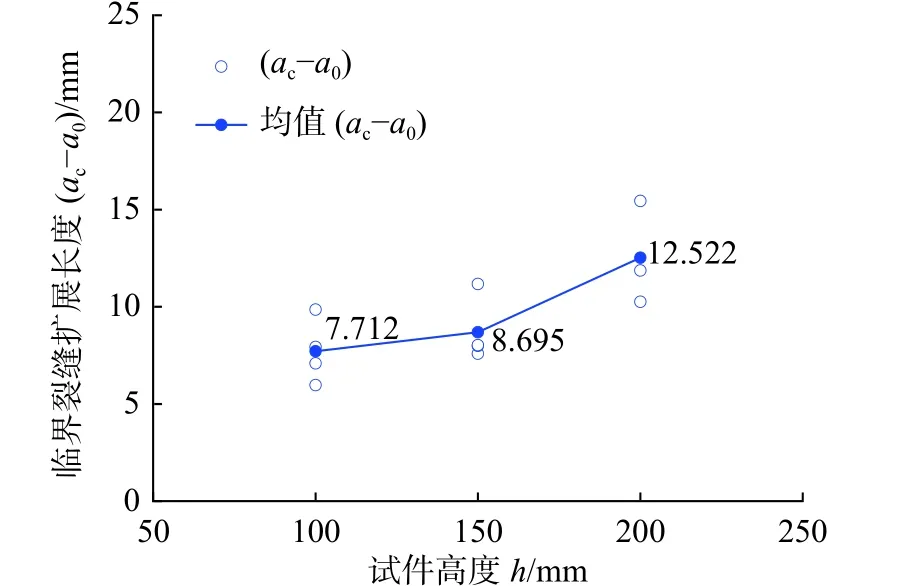
图5 (a c-a0)与试件高度关系Fig.5 Variation of (a c-a0)with depth

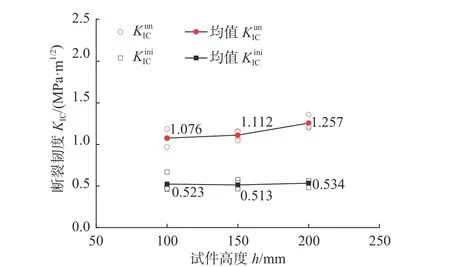
图6 双K 断裂参数与试件高度关系Fig.6 Variations of double-K fracture parameters with depth

3.3 两种方法断裂参数结果比较

3.4 解析法计算起裂断裂韧度比较

如表1所示，实测的CTODc与式(28)计算所得的临界裂尖张口位移CTODCc误差仅一个试件大于15%，可知，式(28)可以用于确定小跨高比三点弯曲梁的CTODc，与文献[39]中结论基本相同。

进而由式(22)计算所得的起裂断裂韧度KIinCi−A如表1所示。图8比较了基于线性插值法与解析法得到的起裂断裂韧度，可见，解析法计算所得结果总体稍大，其平均值为0.552 MPa∙m1/2，较试验法得到结果仅大了5.5%。从而验证了本文所给公式的正确性及解析法对于小跨高比三点弯曲梁的适用性。

3.5 进一步分析

为了进一步验证本文所给出的公式的适用性，参考文献[16, 18]中试验数据，其中，编号为0.2、0.3、0.4 及0.5的各组试件尺寸均为L×h×t=550 mm×200 mm×100 mm，S=500 mm；编号为30的试件尺寸为L×h×t=800 mm×300 mm×100 mm，S=750 mm；编号为TPB300及TPB400各组试件，L=1000 mm，S=900 mm，t=200 mm，h分别为300 mm 和400 mm。材料的具体参数可参考相关文献，这里仅给出初始缝高比a0/h、最大荷载Pmax、临界裂缝张口位移CMODc及计算所得的有效裂缝长度ac、起裂断裂韧度KIinCi及失稳断裂韧度KIuCn结果，分别如表2和表3所示。由于文献[16,18]中未给出起裂荷载，故KIiCni由KIuCn减去文献中所给出的KIcC得到。

由表2知，据本文线性插值法所得的有效裂缝长度ac、起裂断裂韧度KIiCni及失稳断裂韧度KIuCn的结果与文献[16]中所给结果吻合较好，ac较文献[16]中的小，总体差别均小于4.4%；KIiCni与KIuCn的最大偏差分别为4.4%和1.1%。

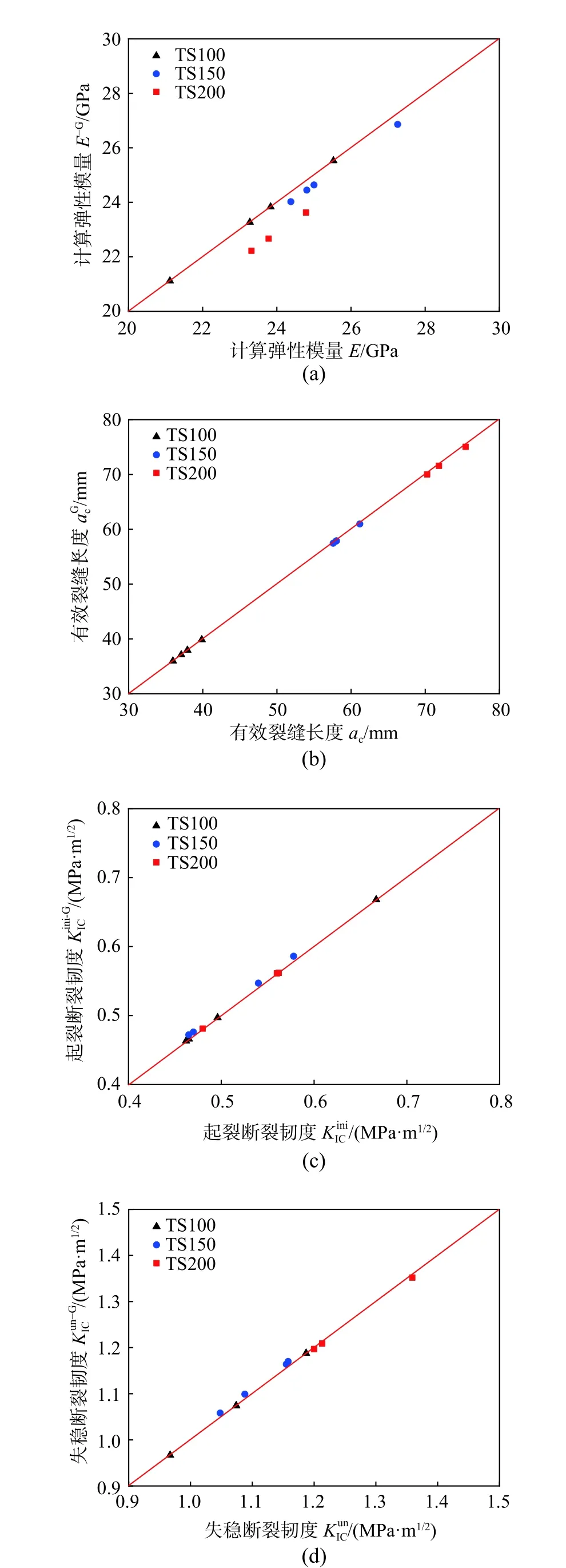
图7 E、a c、KI inCi 及 KI uCn 的结果对比Fig.7 Comparisons of E,a c,KI inCi and K IuCn

图8 KI iCni 的结果比较Fig.8 Comparison of KI iCni

由表3知，据线性插值法所得的相对临界有效裂缝长度ac/h、起裂断裂韧度KIiCni及失稳断裂韧度KIuCn的结果总体较文献[18]稍大，对于ac/h的偏差均在9.5%以内，最大差值为TPB300-1的0.027；KIinCi的最大偏差为TPB400-3时的15.6%，即0.168 MPa∙m1/2；而对于KIuCn的偏差均在9.2%以内。KIiCni的最大偏差稍大可能是由文献[18]中粘聚断裂韧度的计算误差较大所致。

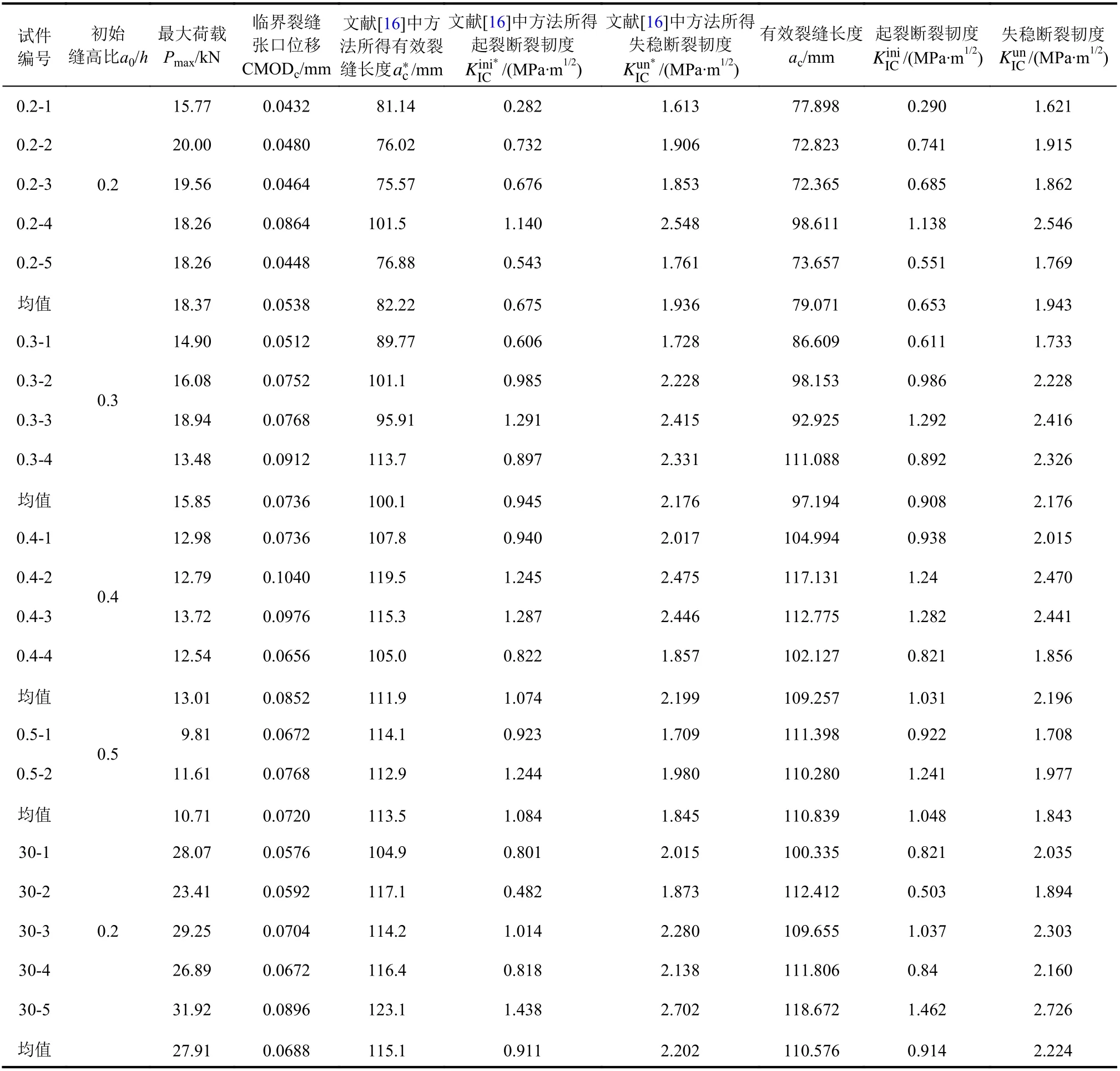
表2 断裂参数计算结果Table 2 Results of fracture parameters

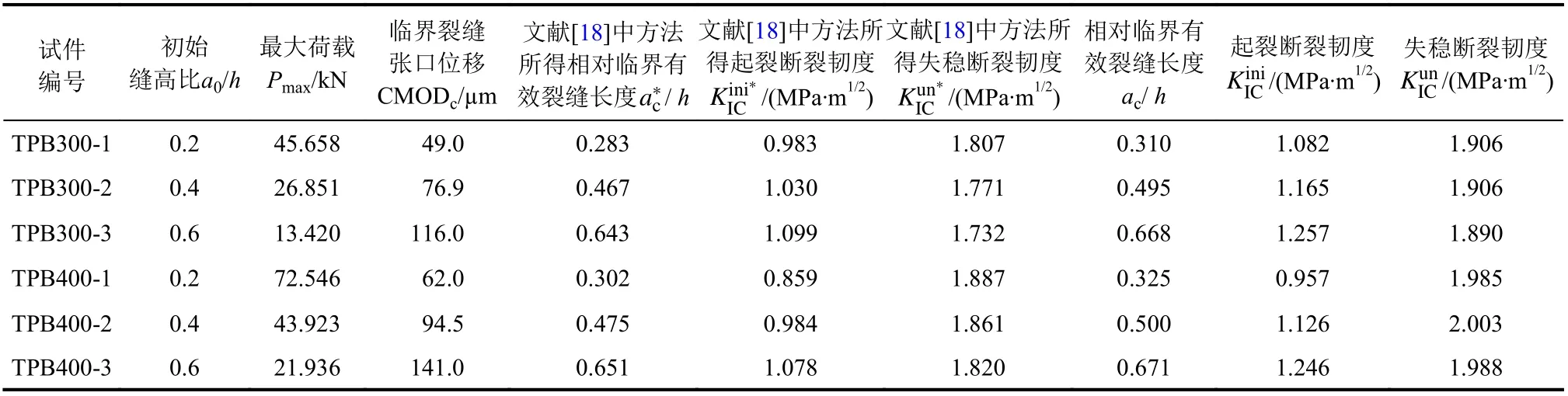
表3 断裂参数计算结果Table 3 Results of fracture parameters

4 结论

(4)通过对文献中已有数据的分析，进一步证明了本文所给出公式可以用于研究小跨高比三点弯曲梁试件的断裂性能。

最后，本文所给的方法有望为研究腐蚀环境下混凝土、价格较昂贵的新材料及不宜加工的岩石材料的断裂性能而采用小跨高比三点弯曲梁(如跨高比为2.5或3)时提供参考。