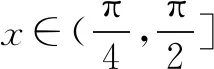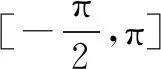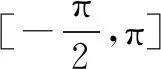例谈一类三角混合题的求解策略
黄智锐 江中伟
(广东省梅州市虎山中学 514299)
近几年来,全国和各省高考对三角函数部分的考查,在内容、题量、分值三个方面保持相对稳定的同时,加大了对三角函数和其他函数结合的一类新函数的考查,难度较大,往往都是压轴题. 这样的命题意在考查考生的计算能力、演绎推理能力、综合应用知识解决问题的能力以及数学思想方法的应用,激发学生进一步学习的潜能. 近几年来不断在高考的相关问题中出现,成为高考题型中的一个创新,仅供参考.
一、sinx、cosx或tanx与一次函数的和或差相结合
此题型形如f(x)=asinx+bx+c、f(x)=acosx+bx+c或f(x)=atanx+bx+c(a,b,c∈R).
例1 设函数f(x)=ax-sinx.若a=1,求曲线y=f(x)在点(π,f(π))处的切线方程.
解析由已知得f(x)=x-sinx,求导得f′(x)=1-cosx,因为f(π)=π,f′(π)=2,故所求的切线方程为y-π=2(x-π),即y=2x-π.
点评根据导数的几何意义求解切线方程.
例2 设函数f(x)=3x+2cosx,g(x)=(ex-1)(e2x-5),若∀x1∈(-,0],∀x2∈R,f(x1)+a≤g(x2),则实数a的取值范围是( ).
解析因为f′(x)=3-2sinx>0,所以f(x)在(-,0]上为增函数,所以f(x)max=f(0)=2.令t=ex(t>0),则h(t)=(t-1)(t2-5),h′(t)=(t+1)(3t-5).当时,h′(t)<0;当t>时,h′(t)>0.所以从而依题意可得即故应选D.
点评求导,确定f(x)max=f(0)=2,然后换元,构造函数求出g(x)=(ex-1)(e2x-5)的最小值,利用f(x)max+a≤g(x)min,列不等式求实数a即可.
请同学们思考:
1.若∀x1∈(-,0],∃x2∈[-1,1],其余条件不变,则实数a的取值范围是____.
2.若∃x1∈(-,0],∃x2∈[-1,1],其余条件不变,则实数a的取值范围是____.
3.若∃x1∈(-,0],∀x2∈[-1,1],其余条件不变,则实数a的取值范围是____.
二、sinx、cosx或tanx与二次函数的和或差相结合
此题型形如f(x)=asinx+bx2+cx+d、f(x)=acosx+bx2+cx+d或f(x)=atanx+bx2+cx+d(a,b,c,d∈R).
例3 设函数f(x)=cosx+kx2+(2k-1)x(x∈R).
(1)证明:对∀k∈R,函数f(x)都不是奇函数;

解析(1)假设函数f(x)为奇函数,因为x∈R,所以f(0)=0,这与f(0)=k·02+cos0+(2k-1)·0=1矛盾.故对∀k∈R,函数f(x)都不是奇函数.

点评(1)采用反证法,假设f(x)为奇函数,则必有f(0)=0与f(0)=1矛盾,故假设不成立,即可证明f(x)不是奇函数;

三、sinx、cosx或tanx与三次函数的和或差相结合
此题型形如f(x)=asinx+bx3+cx2+dx+e、f(x)=acosx+bx3+cx2+dx+e或f(x)=atanx+bx3+cx2+dx+e(a,b,c,d,e∈R).
例4 设函数f(x)=ax-sinx.当a≤1,x∈[0,+)时,证明:
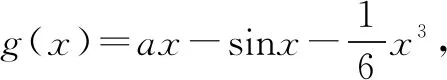
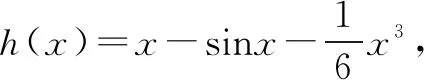
四、sinx、cosx或tanx与指数函数的和或差相结合
例5 已知函数f(x)=ex-cosx.
(1)求函数f(x)在点(0,f(0))处的切线方程;
综上,采用经阴道联合彩超检查剖宫产子宫瘢痕妊娠有着较高的确诊率,其诊断快捷、方便、易操作,患者检查痛苦少易于接受,可以作为早期诊断剖宫产子宫瘢痕妊娠的首选方式,值得推广。
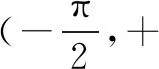
解析(1)∵f(x)=ex-cosx,则f′(x)=ex+sinx,∴f(0)=0,f′(0)=1.故函数f(x)在点(0,f(0))处的切线方程y=x.
(2)当x>0时,ex>1≥cosx,此时f(x)=ex-cosx>0,所以函数f(x)在(0,+)上没有零点.又f(0)=0,下面只需证明函数f(x)在上有且只有一个零点.构造函数g(x)=f′(x)=ex+sinx,则g′(x)=ex+cosx.当时,g′(x)>0,所以函数g(x)在上单调递增.因为f′(0)=1,由零点存在定理知,存在使得f′(t)=0,且当时,f′(x)<0;当t 点评(1)利用导数研究曲线上某点(x0,f(x0))处的切线方程是基本题型,只需求出f(x0)和f′(x0),然后利用点斜式写出所求切线的方程即可; (2)利用分类讨论思想,当x>0时,ex>cosx来说明函数f(x)在(0,+)上没有零点,并利用函数f(x)的单调性和零点存在定理证明函数f(x)在上有且只有一个零点,结合f(0)=0,可证明函数f(x)在)上有两个零点. 例6 函数f(x)=sinx-ln(1+x),f′(x)为f(x)的导数. 证明:f(x)有且仅有2个零点. ②当0 ③当x1 ④当x>2π时,∵ln(1+x)>lne=1,sinx≤1,∴f(x)>0. 故f(x)有且仅有2个零点. 点评此题是2019年高考理数全国Ⅰ卷第20题第(2)问,用分类讨论的方法结合求导判断函数的单调性,再利用零点存在定理可证得. 点评(1)先对函数求导,再求切线的斜率写出切线方程,即得切线的纵截距. 点评根据导函数的解析式可判断f′(x)为偶函数,利用偶函数图象性质及函数图象的特点即可选出正确答案. 总之,这类三角混合题的求解,无论如何变化,都离不开函数单调性的研究,因此在备考中就应该紧紧围绕这个中心问题,熟练掌握函数求导公式、运用导数工具研究单调性的方法. 进行分类讨论、数形结合、转化与化归等数学思想方法的训练和总结.五、sinx、cosx或tanx与对数函数的和或差相结合

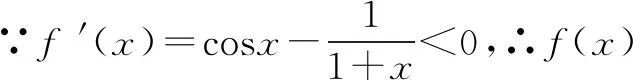
六、 sinx、cosx或tanx与分式函数的积或商相结合
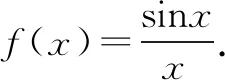
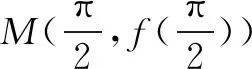
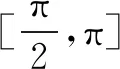
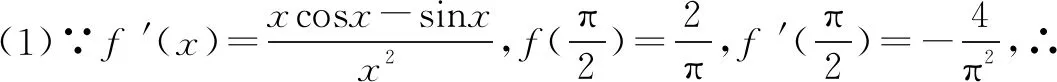

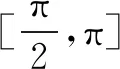
七、形如f(x)=Axmsinx+Bxncosx+C (A、B、C∈R,m、n∈N*)
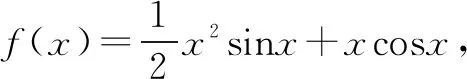

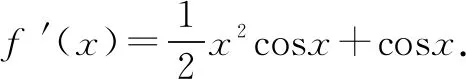
八、sinx、cosx或tanx与其他函数的和差积商相结合