向量是表达几何性质的语言

沈海全

(浙江省绍兴市越州中学 312000)

平面向量是高中数学中重要和基本的概念之一， 也是浙江高考的亮点和难点内容. 它是沟通代数、几何与三角函数的一种工具，有着极其丰富的实际背景,常用平面向量解决一些比较复杂的几何问题，即几何问题代数化.而在高考中某些向量问题常具有丰富的几何背景和几何性质，反而需要把向量问题转化为几何问题，借助几何方法来更好地解决，那就需要我们用敏锐的眼光识别向量语言中所蕴含的几何性质，这也是解决此类问题的难点.本文从课本习题出发通过一系列的拓展变式将一些具有明显几何意义的向量问题进行归纳总结，揭示问题的本质，供老师同学参考学习.

一、在教材中寻根

人教版必修四课本P120 第2,3题.

1.已知向量a，b为非零向量，且|a+b|=|a-b|，求证：a⊥b，并解释几何意义.

2.已知向量a，b为非零向量, 且(a+b)⊥(a-b)，求证：|a|=|b|，并解释几何意义.

下面再看两个小问题.

3.已知向量a，b满足|a|=2，b·(a-b)=0，你能解释其中蕴含的几何意义吗？

4.已知向量a，b满足|a|=2，|b|=|a-b|，你能解释其中蕴含的几何意义吗？

四个简单的向量表达式，蕴含了我们最熟悉的平行四边形、菱形、线段、圆所具有的最美的性质．为变式拓展提供了材料和动力，结合以上性质再加入新的元素|λa-b|设计了这么一个问题. 已知向量a，b满足|a|=2，b·(a-b)=0，|b|=|a-b|，λ∈R，求|λa-b|的最小值.

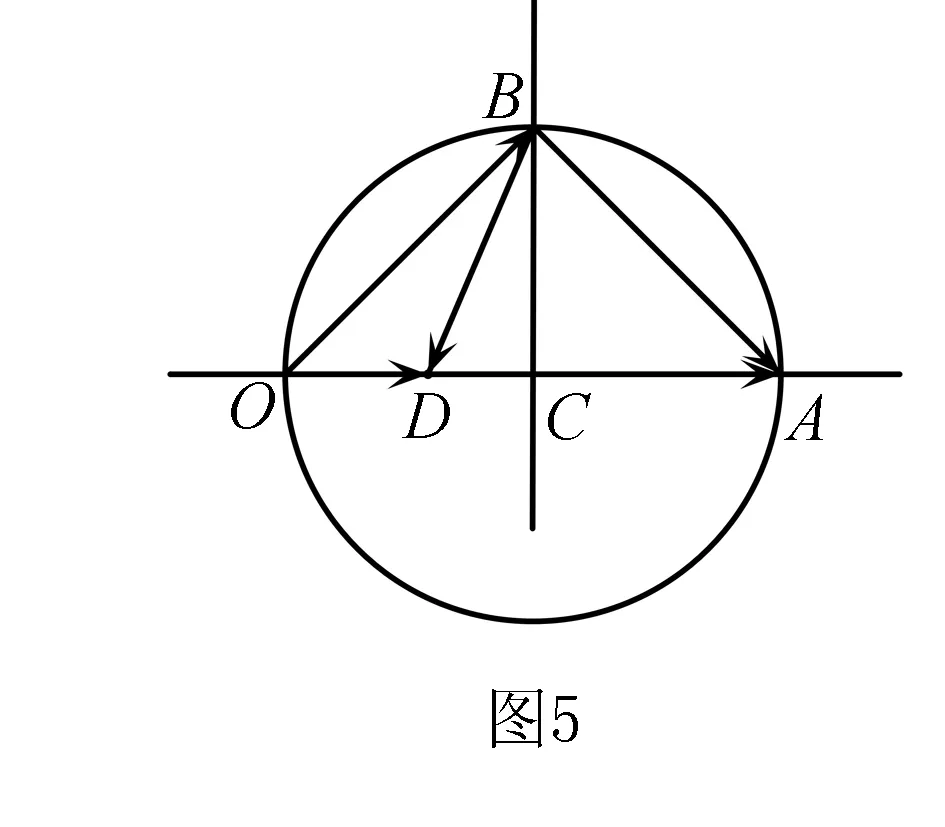
解由以上几个问题可知，b的终点B既在以线段OA为直径的圆周上，又在线段OA的中垂线上，所以b唯一固定，而|λa-b|所表示的几何意义为向量λa终点D和向量b终点B连线距离，即为直线OA上的动点D与定点B连线距离，所以表达的几何意义为直线外一点与直线上一动点的最小距离，即|BD|min=|BC|=1.

二、在根基中求变

问题1已知向量a，b满足|a|=2，a与a-b的夹角为60°，求|b|的最小值.

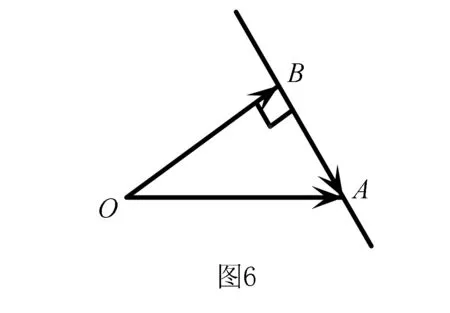
以上问题源于2010年浙江高考试题，体现了直线外一点到直线上动点连线的最短距离为垂线段长度.下面将条件a与a-b的夹角为60°改为b与a-b的夹角为120°,惊喜的发现b终点的轨迹由射线变为了圆弧，而初中已经知道圆最优美的几何性质是同弧所对的圆周角相等.这么优美的几何性质以向量语言表现出来了.而解决这个问题又可以用正弦定理来解决，从而又用到了三角形最美的性质即正弦定理.下面给出问题和解答.

问题2已知向量a，b，c满足|a|=|b|=2，a⊥b，c=λa+(1-λ)b，λ∈R，求|c|的最小值.

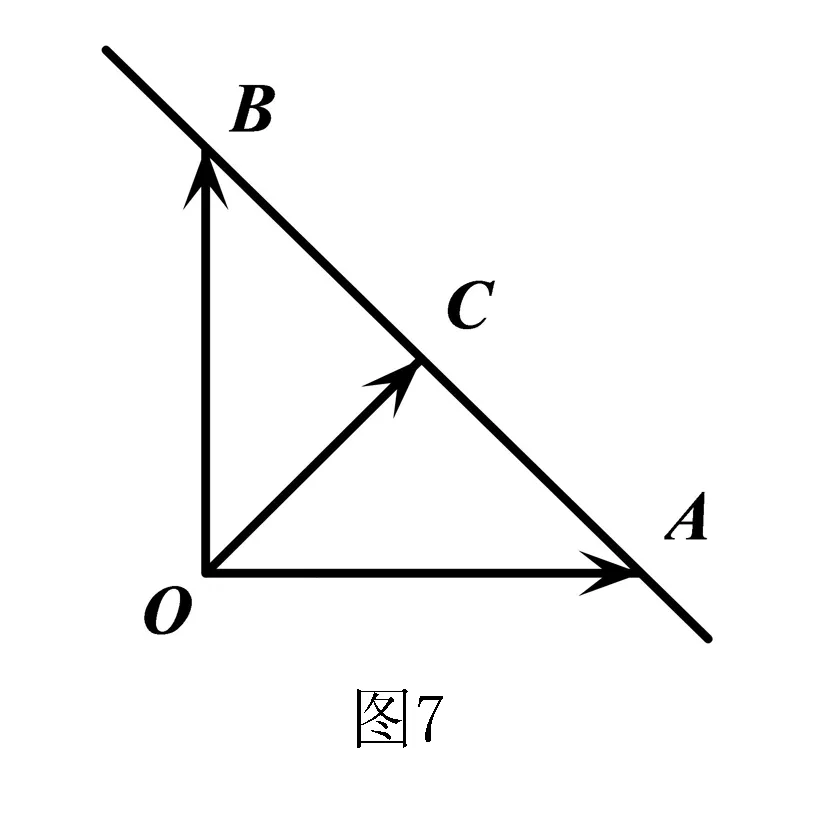
问题2是在问题1的基础上再加进一个新的向量c，向量表达式c=λa+(1-λ)b体现了三点共线.变式1-4对各条件和角度进行了改变，产生了不同的几何性质，变式5更大胆地让c也运动起来，最后转化为两圆相切问题.有了以上的探究，下面对2018年浙江高考平面向量试题进行分析,原来试题是那么自然而漂亮.

三、在真题中实践

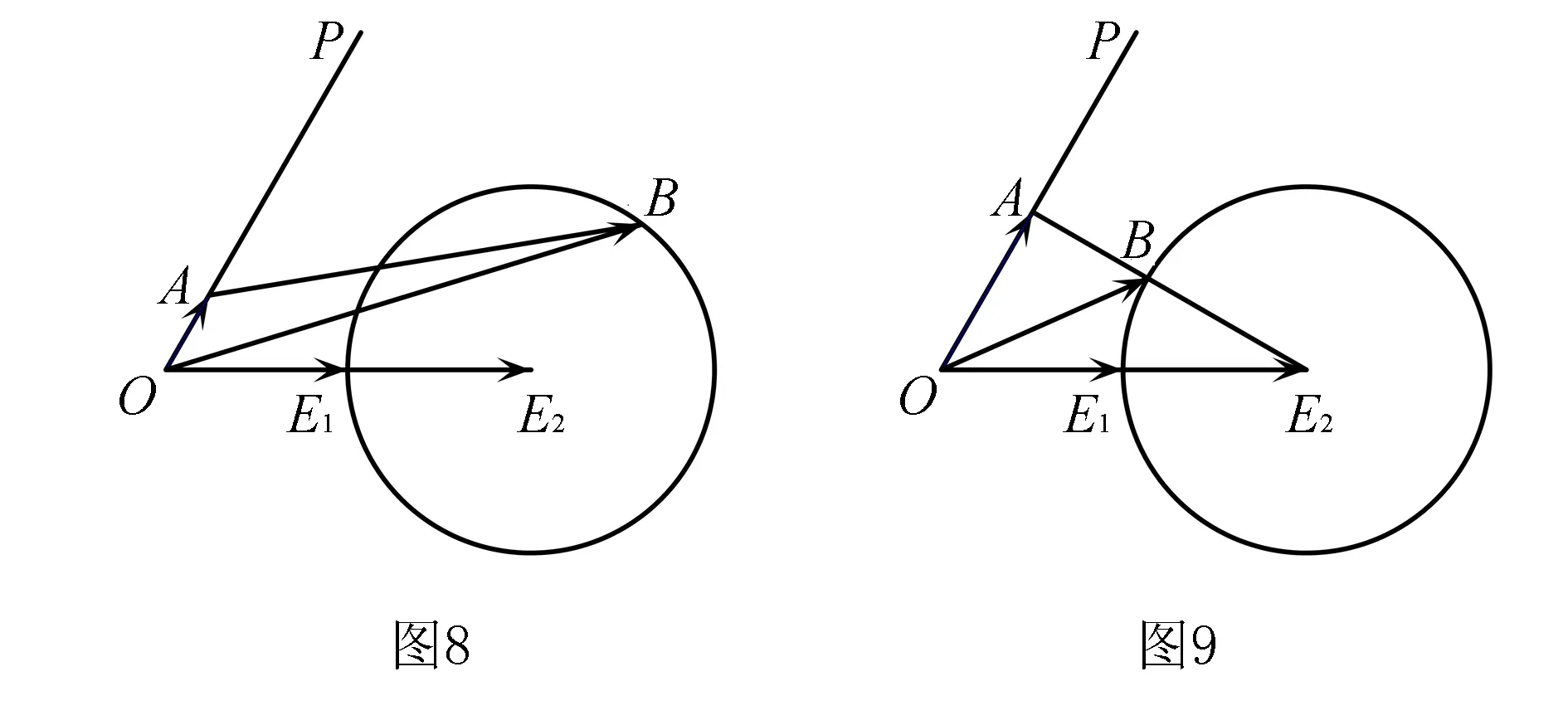
(b-e)·(b-2e)=0，即(b-e)⊥(b-2e).所以b的终点在以E1E2为直径的圆周上.下面同解法一.

著名的艺术家罗丹说：“美到处都有，生活中不是缺少美，而是缺少发现美的眼睛.”本文中简洁的向量表达式展现了平面几何中一些最美的性质.这就需要教师在高考复习过程中精心选择教学复习材料，精心设计教学过程.在教学过程中要注意知识发现的过程，让学生体会知识的来龙去脉，使学生在发现知识的过程中，经历探究、思考、加工的过程，实现知识的“表象特征”到“内在价值”理解升华.着力让学生数学能力数学素养在数学问题的解决过程中生成、在教学互动的过程中成长、在思维思辨过程中升华.