基于测点优选和改进L曲线法的动载荷识别

李晓旺， 赵海涛， 陈吉安

(上海交通大学 航空航天学院， 上海 200240)

动态载荷识别[1]是结构动力学中的第2类反问题.目前，载荷识别方法主要有频域法、时域法以及其他一些智能算法[2-4].对于每一种算法而言，其最终目的都是要建立起输入载荷和输出响应以及系统特性之间的数学模型.由于反求输入载荷的过程需要对数学模型中的传递函数矩阵求逆，并且被测响应容易受到环境噪声的干扰，往往会导致出现不适定问题.

为了尽量减小传递函数矩阵的病态性和响应噪声对载荷识别精度的负面影响，国内外学者做了大量的研究工作.这些研究总体上可分为两种思路：第1种思路为通过优化响应点的位置[5-6]获得病态程度较低的传递函数矩阵，然后直接求广义逆；第2种思路为避免对传递函数矩阵直接求逆，而是通过一定的技术手段对振动方程进行特殊处理，间接反演动态激励，比较典型的方法有奇异值分解(SVD)法[7]和 Tikhonov 正则化方法[8].对于正则化方法来说，如何选择正则化参数是关键，而L曲线法[9-10]是最为常用的计算正则化参数的方法.

然而，目前的研究鲜见将两种思路结合起来.对此，本文提出在时域中分2步解决不适定问题.第1步对不同测点对应的传递函数矩阵进行分析，找出条件数最小的传递函数矩阵，从而获得最佳测点.第2步采用Tikhonov正则化重构载荷.同时，针对正则化方法精度不高的缺点，在确定正则化参数的过程中对L曲线法进行改进，即引入B样条函数[11]对L曲线进行插值，并通过计算B样条曲线的各点曲率获得更加准确的正则化参数.

1 基于Taylor多项式迭代的载荷识别方法

采用Taylor多项式迭代法[12]在时域内识别载荷时间历程.对于一个多输入多输出的振动系统，其振动微分方程可表示为

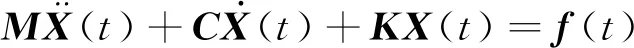
(1)

为了将振动方程解耦，总时间历程被离散成n个时刻.对于任意相邻的第i时刻t和第i+1时刻t+Δt，t+Δt时刻的振动响应被近似地表示为t时刻响应的Taylor多项式展开形式，即

(2)

(3)

(4)

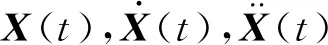
(5)

式中：A1,A2,Ad,Av,Aa,B1,B2,Bd,Bv,Ba,D1,D2,Dd,Dv,Da均为m×m阶定常矩阵；下标a，d，v分别为加速度、位移和速度；F为从t1～tn+1时刻的全部激励组合.

设结构自由度数为m，则对式(5)作递归可得到总线性离散方程为

(6)

式中：Yl为从t1～tn时刻的全部响应组合；Hl为总体传递函数矩阵.

2 载荷时间历程重构

2.1 响应测点的优选方法

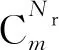
(7)

通过遍历全部组合情况可以找到条件数最小的传递函数矩阵H，此时的测点组合Y即为最佳选择，从而实现了响应测点的优化配置.

2.2 改进的L曲线法

在获得最佳测点的响应值并确定了条件数最小的传递函数矩阵之后，采用Tikhonov正则化技术重构式(6)中的输入载荷.设系统误差e为

e=Y-HF

(8)

引入罚函数J的概念

J=(eTe)+λ(FTF)

(9)

当J对F的1阶导数为0，误差e达到最小值.此时激励F可以表示为

F=(HTH+λI)-1HTY

(10)

式中：I为单位矩阵；λ为正则化参数.

正则化技术的核心在于如何选择合适的正则化参数λ，L曲线法是常用的一种计算λ的方法.该方法的思路是选取一系列不同的λ值，分别计算每一个λ所对应的lg‖Y-HF‖和lg‖F‖值.然后以lg‖Y-HF‖为横坐标，lg‖F‖为纵坐标作图，其曲线形状类似于字母“L”.在L曲线的拐点位置可找出曲率最大的一个点，该点对应的λ值即为最合适的正则化参数.

然而，传统的L曲线法存在一定的缺陷.首先，该方法的第1步对λ值的选取具有一定的盲目性，很可能会遗漏最准确的λ值.其次，由于受到矩阵H奇异性的影响，对lg‖Y-HF‖和lg‖F‖求1阶和2阶导数很容易偏离真实值，从而直接造成L曲线的曲率计算结果不可靠.

为弥补上述不足，本文建立了基于B样条插值的改进L曲线算法.首先依据常规方法获得L曲线，然后截取L曲线的拐点部分(L-Co)进行插值操作，最后计算B样条各点曲率从而获得最佳正则化参数.

2.2.1L-Co的B样条插值 设L-Co共有Nc个坐标，第j个坐标为(xj，yj)，其对应的正则化参数为λj，则共可以组成Nc个B样条插值函数的控制顶点，任意一个控制顶点Pi可表示为

(11)

(i=0,1,…,Nc-1)

对L-Co进行k次B样条插值后，曲线可写为

(12)

0≤u≤1

式中：Ni,k(u)为定义在节点矢量U=[u0u1…uNc+k]上的k次B样条基函数，Ni,k(u)的计算公式为

(13)

(14)

经过B样条插值操作后，L-Co涵盖的λ值远远超过预先选取的控制点的数量，避免了遗漏最佳正则化参数的可能.与选取同样数量λ值计算L曲线坐标的传统方法相比，B样条插值操作的计算量要小的多.

2.2.2L-Co的各点曲率求解 经过插值操作后，计算L-Co各点的曲率问题可以转化为计算B样条函数的曲率问题.对k次B样条曲线求1阶导数的公式为

(15)

令

则式(15)可以改写为

(16)

将式(16)和(12)比较可知，k次B样条曲线的1阶导数恰好是一条新的k-1次B样条曲线.因此，求S(u)的2阶导数只需根据式(15)计算S′(u)的1阶导数即可求出S″(u)的值.插值后的L-Co是一条二维平面曲线，所以S′(u)和S″(u)分别对应坐标(x′，y′)和(x″，y″)，则L-Co各点的曲率Cu的计算公式为

(17)

曲率最小值所对应的λ值即为最优正则化参数，代入式(10)可以重构输入载荷.

3 数值算例研究

为验证所提方法的可行性和有效性，建立了3个不同的数值算例.3个算例所施加载荷的数量和复杂程度逐渐增加，扰动噪声的水平也依次升高.采用本文算法分别对3个算例的输入载荷进行重构，并与最差测点识别结果以及奇异值分解法识别结果进行对比.

3.1 正弦载荷识别算例

算例(T)1建立了一个悬臂梁模型，悬臂梁各项参数分别为弹性模量E=70 GPa，泊松比μ=0.35，密度ρ=2 700×103kg/m3，长宽高尺寸为600 mm×60 mm×30 mm.受正弦激励的悬臂梁模型如图1所示，对悬臂梁模型施加2个正弦时变载荷，2个动态激励可表示为

(18)

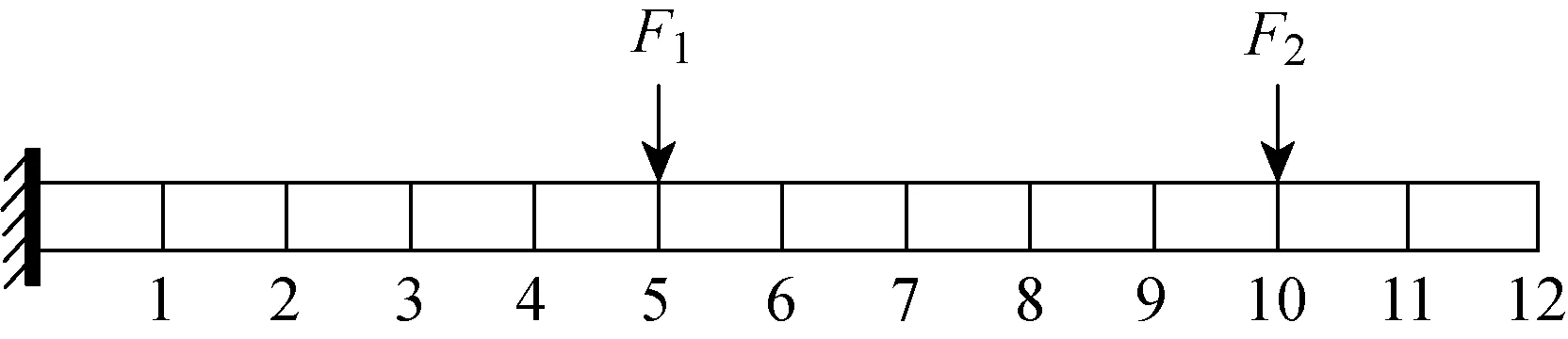
图1 受正弦激励的悬臂梁模型

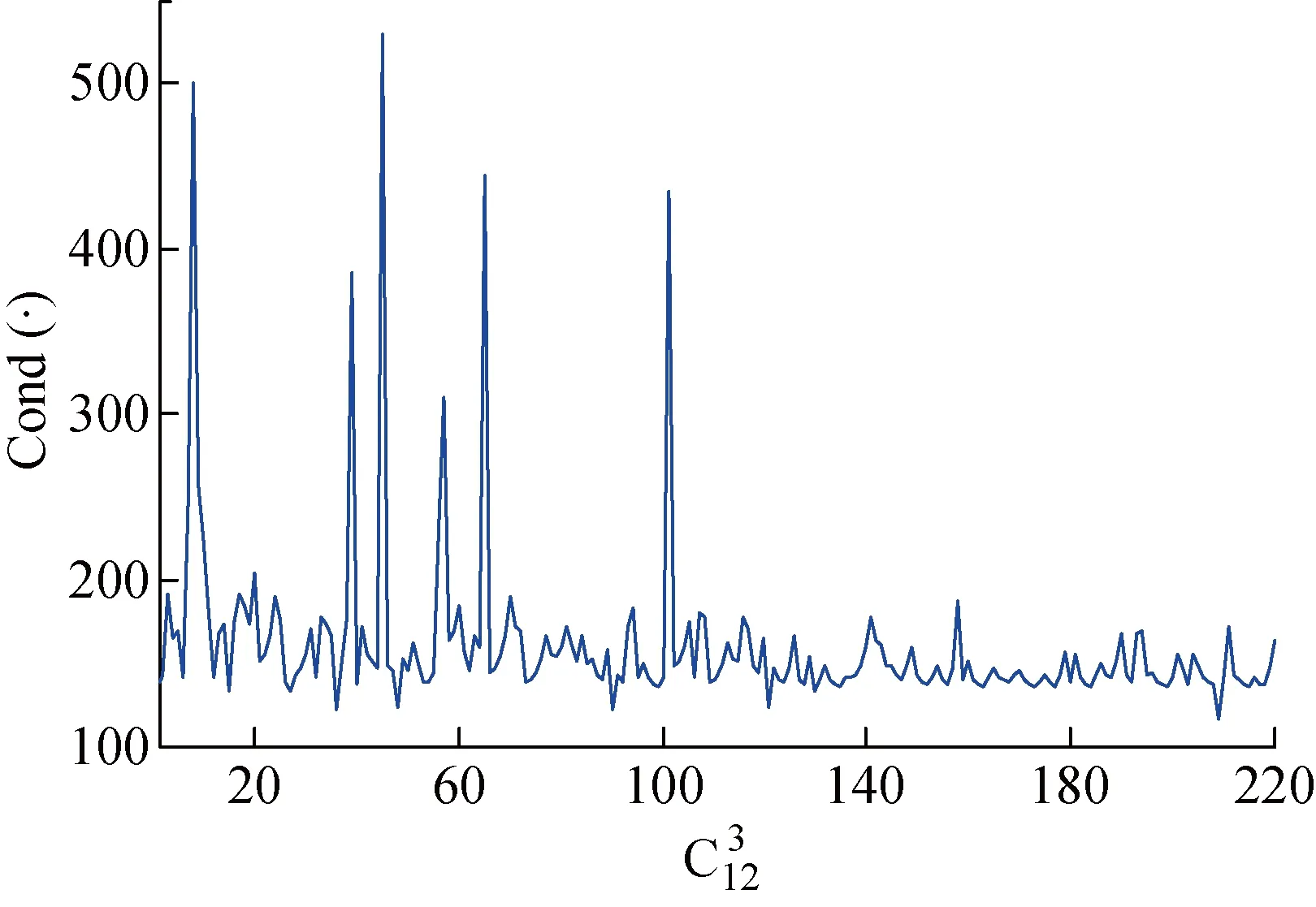
图2 T1中不同测点组合对应的条件数

根据图2可知，第209种组合情况可获得最小条件数为97，对应最佳测点为7、10、12；第45种组合情况可获得最大条件数为441，对应最差测点为1、7、12.

在分别获得最佳测点和最差测点的响应值前提下，对被测响应混入5%的Gaussian白噪声.采用改进的L曲线法计算最佳测点下的最佳正则化参数λ.T1中的整体L曲线如图3所示，对L-Co进行B样条插值的结果如图4所示，所有λ对应的L-Co曲率如图5所示，其中Cu为曲率.

由图5可知，当λ=9.87×10-6时，L-Co的曲率达到最大值.将该λ值代入式(10)，即可反求输入载荷的时间历程.本文方法和两种对照方法的识别结果如图6所示，其识别误差如表1所示.

由图6可知，本文算法对正弦载荷的识别结果与真实值吻合得较好.由表1可知，本文算法的识别误差低于另外两种算法.同时，SVD法的识别误差也保持在较低水平，低于选用最差测点的识别误差.这说明对于载荷数量较少且形式简单、噪声影响水平较低的载荷识别问题来说，SVD法也可以适用，测点的选取对识别精度的影响要大于不同重构算法的影响.

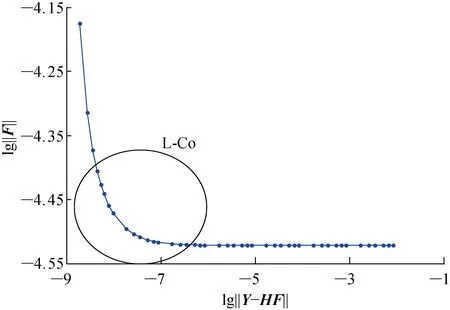
图3 T1的L曲线图

图4 T1中L-Co的B样条插值结果

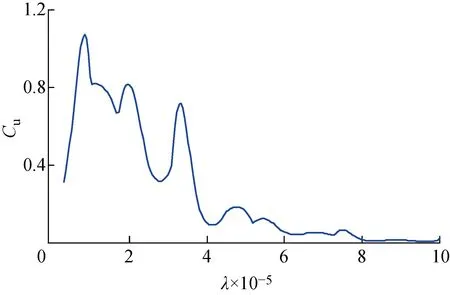
图5 T1中L-Co各点曲率计算结果

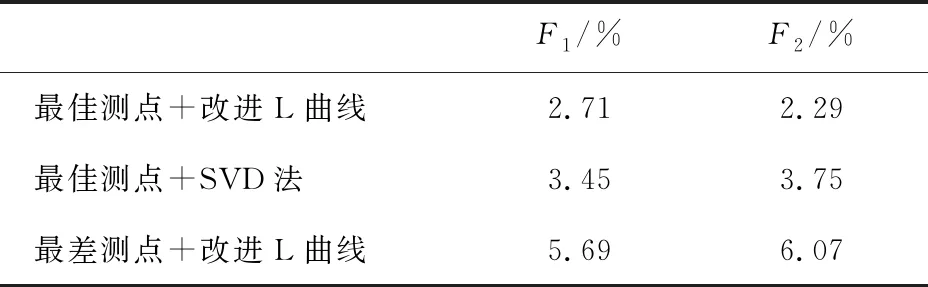
表1 T1载荷识别误差

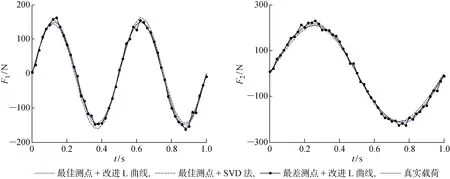
图6 T1载荷时间历程重构结果

3.2 正弦叠加载荷识别算例

T2选用和T1相同的悬臂梁模型，该结构受到3个正弦叠加载荷的激励，受力情况如图7所示.

3个动态激励的表达式为

(19)

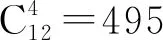
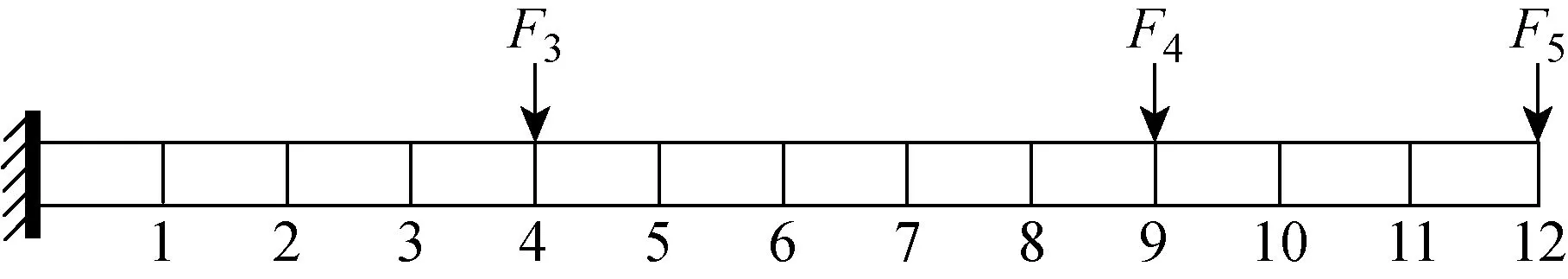
图7 受正弦叠加激励的悬臂梁模型

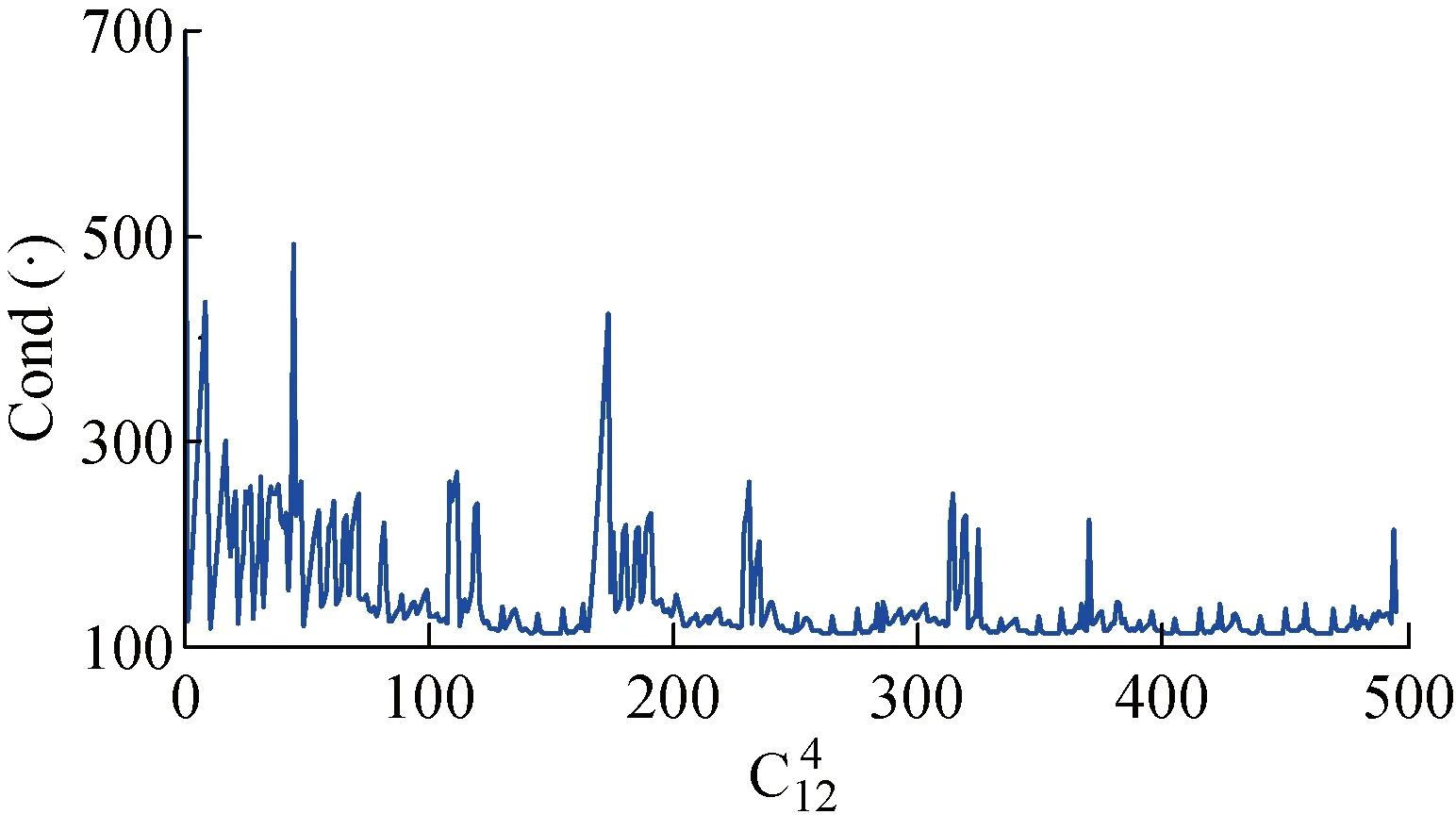
图8 T2中不同测点组合对应的条件数

依据图8所示的计算结果，当组合数为271时，得到最小条件数为112，对应的最佳测点为2、7、9、11；当组合数为1时，得到最大条件数为811，对应的最差测点为1、2、3、4.

接下来通过仿真获得最佳测点和最差测点的响应值，对响应混入10%的Gaussian白噪声.采用改进的L曲线法计算最佳正则化参数λ.图9～11分别为T2的L曲线图、B样条插值后的L-Co图，以及L-Co的曲率图.

根据图11中的曲率计算结果，当λ=2.06×10-5时，L-Co的曲率获得最大值.将该λ值代入式(10)重构3个正弦叠加激励的时间历程.动载荷的识别结果如图12所示，其识别误差e如表2所示.

表2 T2载荷识别误差

图9 T2的L曲线图

图10 T2中L-Co的B样条插值结果

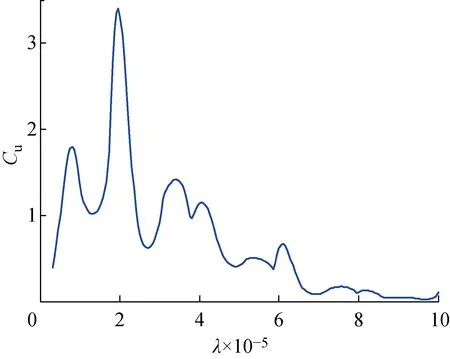
图11 T2中L-Co各点曲率的计算结果

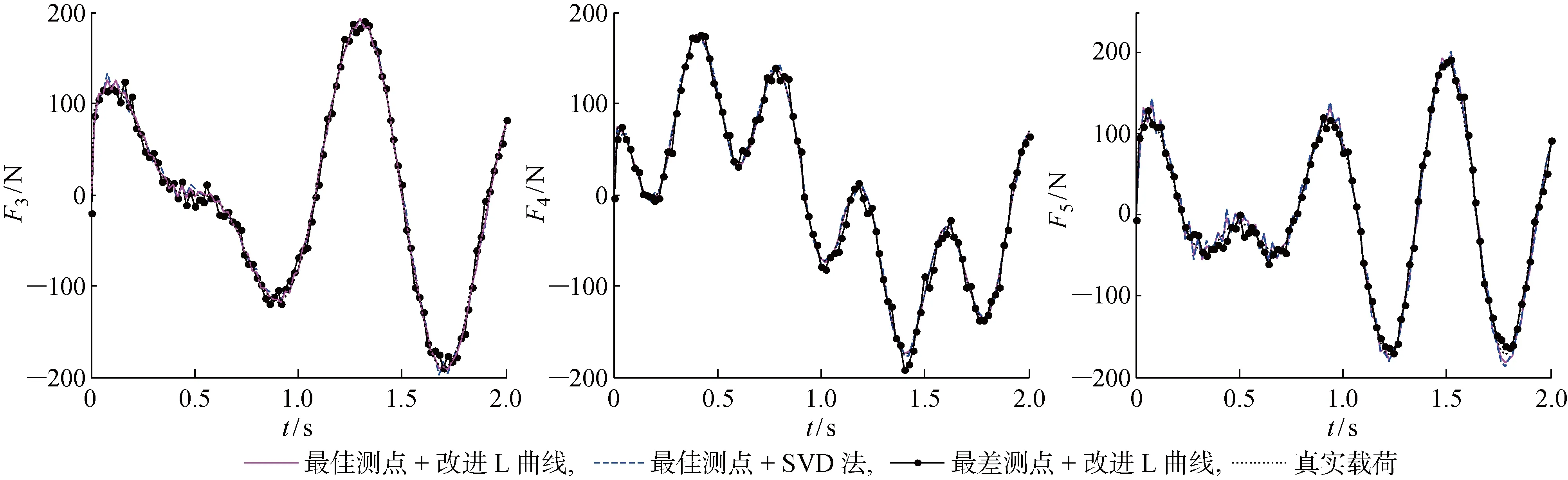
图12 T2载荷时间历程重构结果

由图12可知，本文算法可以较为准确地反演出正弦叠加激励的时间历程，其识别结果相比于另外两种算法更靠近真实载荷.从表2可以看出，由于T2的载荷复杂度、载荷数量以及噪声水平均高于T1，导致算法的识别误差比T1有所提高.而从数据值来看，3个载荷的识别误差均在6%以下，仍属于较低水平且低于两种对照算法的误差，体现了所提算法的优越性.

3.3 Gaussian白噪声载荷识别算例

T3建立了一个桁架模型，其各项参数为E=200 GPa，μ=0.3，ρ=7 800×103kg/m3，截面积为20 cm2，所有水平桁架和竖直桁架的长度均为1 m.对桁架模型施加4个Gaussian白噪声载荷，载荷幅值分别为80 N、70 N、60 N、50 N，如图13所示.

由图14可知，当测点组合数为595时，条件数取到最小条件数为194，对应的最佳测点为3、4、9、11、12；当组合数为109时，条件数取到最大条件数为 1 215，其对应的最差测点为1、2、7、10、12.

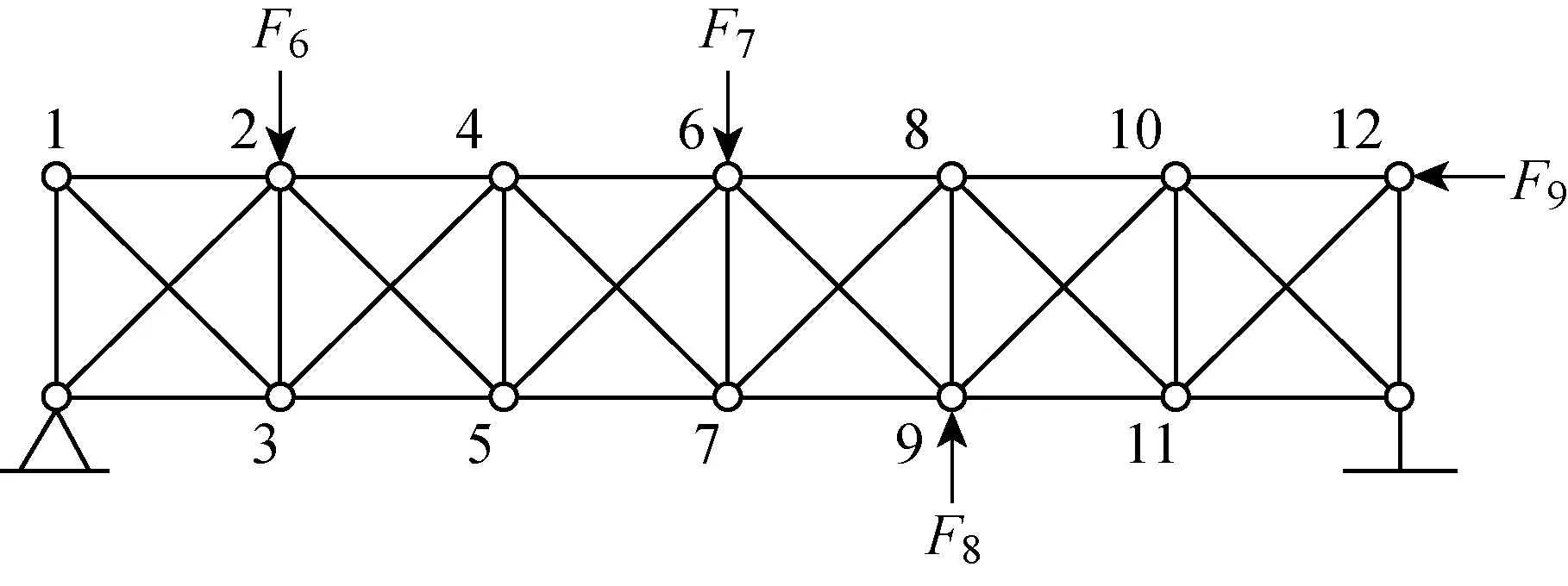
图13 受Gaussian白噪声激励的桁架模型

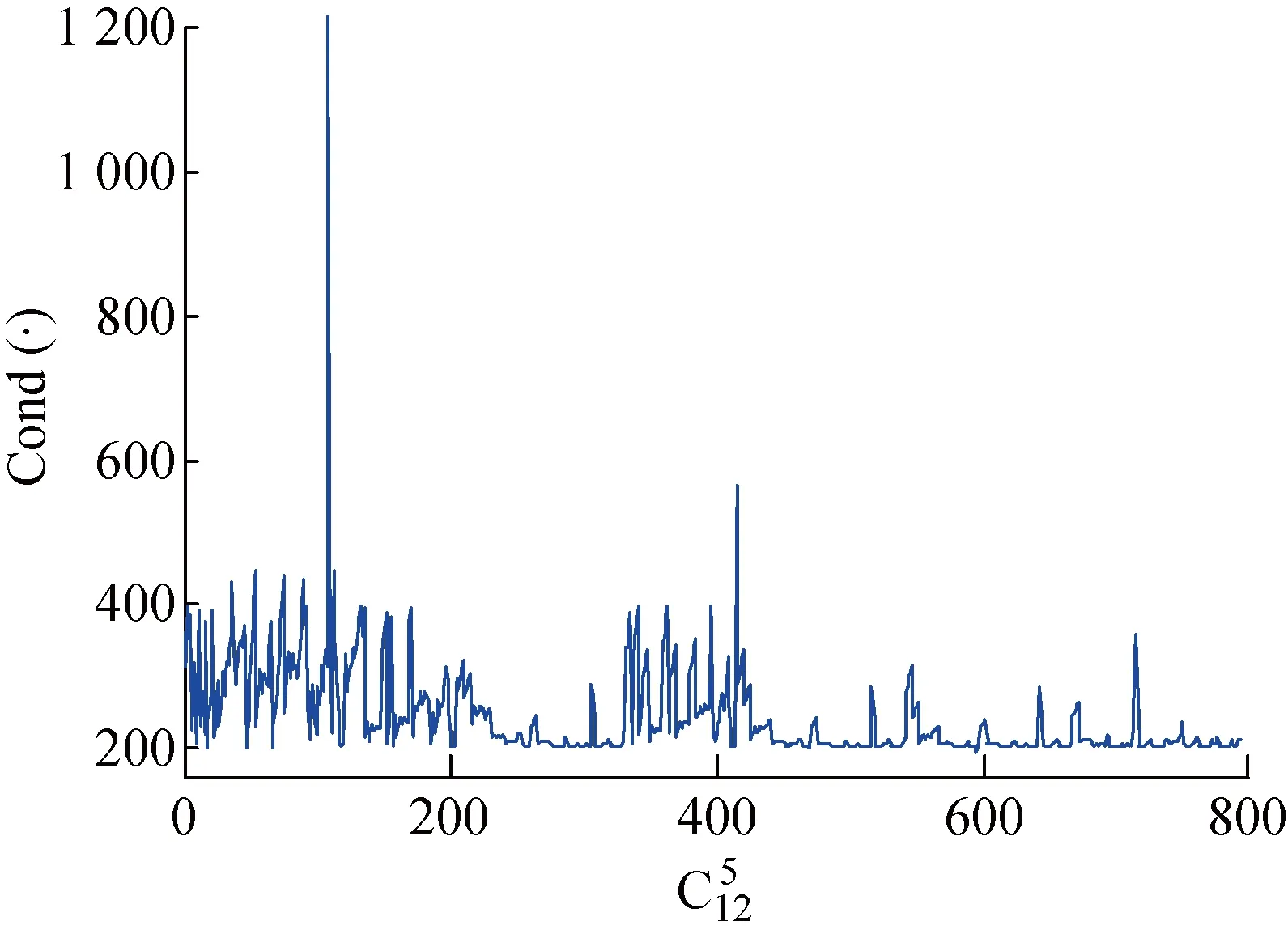
图14 T3中不同测点组合对应的条件数

对被测响应混入15%的Gaussian白噪声，然后采用改进的L曲线法求解正则化参数λ的最佳值.图15～17分别为T3的L曲线图、B样条插值后的L-Co图，以及L-Co的曲率图.

由图17可知，当L-Co的曲率达到最大值时，对应的最佳λ值为4.91×10-5.根据式(10)重构输入激励，T3的载荷重构结果如图18所示，其识别误差如表3所示.

与前两个算例相比，T3的Gaussian白噪声激励是时变载荷中复杂程度最高的一种.从图18中的被识别激励时间历程曲线可以看出， 本文算法重构的载荷与真实值的吻合程度显著高于其他两种对照算法，说明该算法具有优越的稳健性和抗噪性.由表3可知，本文算法的识别误差虽然比T1和T2稍高，但仍处于较低水平且明显低于对照算法.由于载荷数量较多，导致传递函数矩阵维数较大，即使选取最佳测点也有较强的病态性，从而引起SVD法的识别误差迅速增大，此时不同识别算法对精度的影响超过了测点的选取对精度的影响.

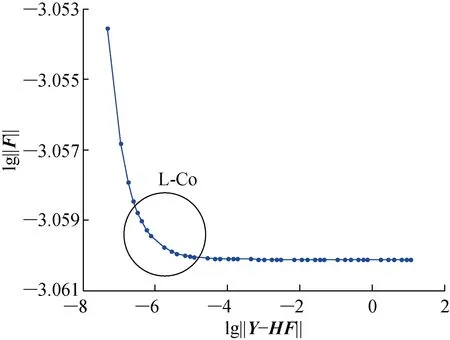
图15 T3的L曲线图

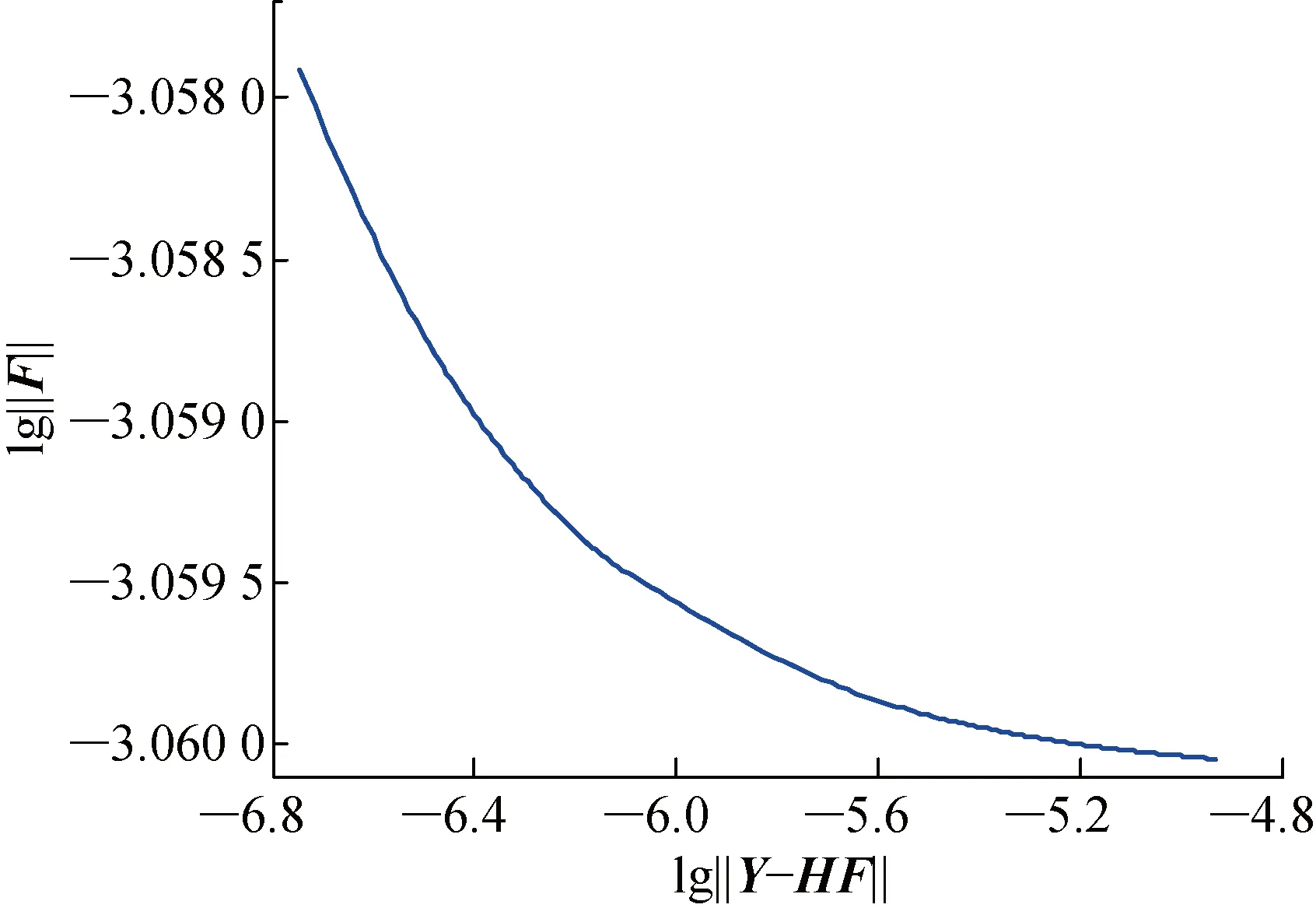
图16 T3中L-Co的B样条插值结果

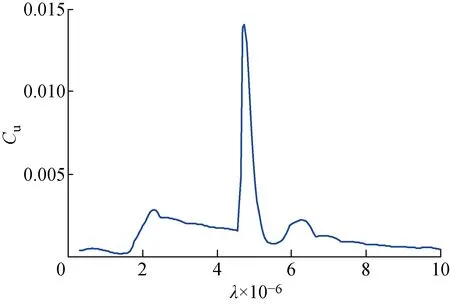
图17 T3中L-Co各点曲率计算结果

图18 T3载荷时间历程重构结果

表3 T3载荷识别误差

4 结语

针对载荷识别中的不适定问题，在时域内建立了测点优选和改进的L曲线法相结合的算法.首先通过遍历所有测点组合找出条件数最小的传递函数矩阵，进而获得对应的最佳测点.然后在使用正则化方法反求输入载荷的过程中引入二次B样条函数对L曲线进行插值，从而获得了更加精确的正则化参数，并将该算法的载荷重构结果分别与最差测点识别结果以及SVD法识别结果作对比.数值算例结果表明，该方法可以有效减弱传递函数矩阵的病态性，并具有较强的稳健性和抗噪性，从而提高了载荷识别的精度.