DWT-Schur结合的全盲数字视频水印算法

包宋建，杨守良

(重庆文理学院 电子电气工程学院， 重庆 402160)

随着博客、视频网站和社交网络的应用与发展,数字视频和图片在互联网上的传播越来越广，对数字内容版权的保护越来越有必要。在多媒体中，数字水印已成为保护数字数据最有效的技术。采用水印技术在数字媒体内容中，通过嵌入一个小的版权信息,可以确定其所有权，因此实用的水印技术需考虑不可感知性和算法的鲁棒性。不可感知性是指水印知觉透明度,而鲁棒性是指在有意或无意的攻击下(如退化、裁剪、滤波或添加噪声)从数字媒体中提取被嵌入的水印的能力[1-2]。

很多学者在转换域中对音频、图像和压缩解压视频的水印算法进行了研究，这些算法使用了流行的变换方法,例如，奇异值分解(SVD)、离散小波变换(DWT)和离散余弦变换(DCT)等。也有很多算法把这些变换方法进行混合，以获得更好的嵌入和提取效果。目前，在一些新的研究中，把舒尔变换应用于水印技术中，与其他变换域方法相比，其鲁棒性和精度更好。

文献[3]提出了一种使用舒尔和奇异值分解转换的非盲混合水印方案，在水印的嵌入和提取的步骤中使用了舒尔分解，将图像分解为8×8的块，再应用奇异值分解最大本征值。文献[4]提出了一种使用舒尔和元胞自动机变换(CAT)的非盲混合技术,充分使用了CAT域的灵活性和舒尔转换的效率。文献[5]提出了基于舒尔变换的盲图像水印方法，将图像转化为舒尔变换，然后进行分析,找到一个嵌入过程发生的非敏感区域。文献[6]提出了嵌入水印的2种舒尔分解变换算法，利用D矩阵和U矩阵正交分解,使相同的水印信息存储加倍，提高了算法的鲁棒性。

小波变换是时间(空间)频率的局部化分析，它通过伸缩平移运算对信号(函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。适当地选择基本小波，使其在时域上有限支撑，在频域上也比较集中，便可以使小波变换在时域、频域都有表征信号局部特征的能力，这样就有利于检测信号的瞬态或奇异点。在数字水印的嵌入与提取中利用小波变换的特点可以较好地提高水印无感知性。

由于舒尔变换与小波变换在水印处理中应用广泛，因此提出舒尔分解与离散小波变换相结合的方法来实现具有高鲁棒性和无感知性的高效视频水印技术。

1 离散小波变换与舒尔分解

1.1 离散小波变换

离散小波变换DWT是基于各种频率和有限持续的小波变换，可用于对信号进行频率和空间的描述[7]。采用小波变换对图像进行分解，首先分为高频部分和低频部分，高频部分包含组件的边缘信息,而低频部分又再次分为高频部分和低频部分。由于人眼对图像边缘变化不敏感，因此高频组件通常用于水印。

图1是采用DWT将输入图像分层分解成4个频率区，即：LL、LH、HL、HH，其中LL为低频，LH、HL、HH为分别为水平、垂直和对角线上的高频分量。本文算法采用了两级DWT，在第二级中使用水平细节子图(HL)，每一个子图具有特定分辨率的DWT系数矩阵。图2显示了通过两级小波分解生成的子图。

图1 图像的一级DWT子图

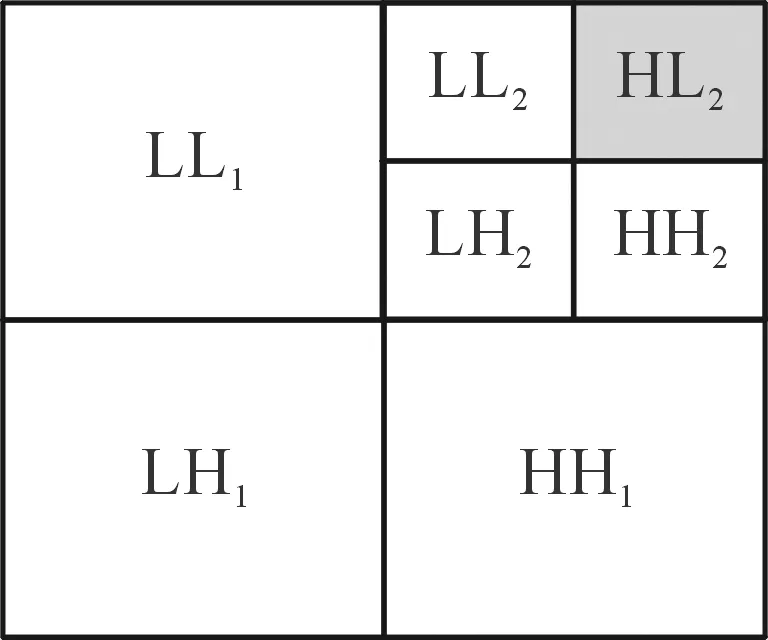
图2 图像的两级DWT子图

1.2 舒尔分解

舒尔分解或舒尔三角化是线性代数中一个重要数学工具，常用于度量分析。舒尔分解也是奇异值分解中一个重要的中间步骤，并且是降低运算量的一种有效方法。对于n×n的矩阵，采用舒尔分解需要约每秒n3次浮点数运算，而奇异值分解则需每秒11×n3次的浮点数运算，这意味着舒尔的计算量要少于奇异值分解计算量[8]。舒尔分解变换有复舒尔分解变换和实舒尔分解变换两种。实舒尔分解是把一个实方阵A分解成如式(1)所示的U矩阵和S矩阵。

Schur(A)=U×S×UT

(1)

式中:S是上三角矩阵块，也被称为实舒尔形式；U是一单位正交矩阵；UT代表U的共轭转矩。下面通过一个4×4矩阵A为例子来说明舒尔分解的应用原理。

对矩阵A进行实舒尔分解后，得到矩阵U和矩阵S，如下所示:

显然,S是一个三角矩阵，按矩阵相似性定义，它是矩阵A的相似矩阵。因此，矩阵S具有与矩阵A相同的特征值集。由于S矩阵的特征值集包含在主对角线上，又由于舒尔分解的特征值十分稳定，因此,S矩阵的对角线常用于水印的嵌入。

2 DWT-Schur结合的盲数字视频水印算法

在任何一种数字水印技术中，宿主是水印嵌入的地方。宿主可以是图像、视频或音频。由于视频序列中的每一帧就是一副图像，所以图像水印可以扩展到视频水印[9]。在本文提出的水印技术中，将DWT和舒尔变换相结合，将水印嵌入数字视频中。

DWT-Schur相结合的水印算法由2个过程组成，第一个过程是将水印嵌入原始视频中，第二个过程是从被嵌入视频中提取出水印。下面对这两个过程进行详细描述。

2.1 水印嵌入过程

基于DWT-Schur水印算法首先将选中的二进制水印嵌入视频帧中，嵌入过程及步骤如下：

步骤1输入视频阶段

1) 输入视频片段V。

2) 把视频片段分解成视频场景Vs。

3) 使用DWT 和Schur处理每个视频场景帧，具体步骤如4)～11)所述。

4) 每个视频帧F，从RGB转换为YUV矩阵格式。

步骤2两级离散小波变换阶段

5) 在每一个视频帧F中，对Y(亮度)矩阵进行2级离散小波变换。这个操作生成7个DWT子图(LL1、LL2、HL2、LH2、HH2、LH1、HH1)。

步骤3舒尔分解阶段

6) 舒尔算子应用在HL2子图(突出显示在图2中)。舒尔算子分解子图系数矩阵为2个独立的矩阵:

HL2=(UHL2SHL2)

(2)

步骤4水印嵌入阶段

7) 重新调节水印图像，使得水印的大小与将被用于嵌入的HL2子图大小相匹配。

8) 通过使用SHL2(i,i)的8位最小有效位(LSB)代替水印位Wi，实现水印WVsi的二进制位嵌入SHL2的三角矩阵。

LSB(SHL2(i,i))=WVsi

(3)

步骤5视频重建阶段

(4)

11) 将视频帧f′ 从YUV矩阵转变为RGB矩阵。

12) 重建帧为最终的水印视频场景F′。

13) 重建水印场景得到最终的水印VXM。

2.2 水印的提取过程

水印的提取过程不需要原始视频，本算法是一个全盲算法。因此，可以直接从水印视频帧中最低有效位来提取水印图像。水印提取过程步骤如下：

步骤1输入视频

1) 输入水印视频片段V′。

3) 使用DWT和Schur处理每个水印视频场景的水印帧，具体描述如4)～7)所示。

4) 将视频帧F′从RGB颜色矩阵转变为YUV矩阵。

步骤2应用两级离散小波变换

5) 计算帧F′的两级DWT，产生7个子图:[wLL1、wLL2、wHL2、wLH2、wHH2、wLH1、wHH1]。

步骤3应用舒尔算子

6) 舒尔算子应用于子图wHL2。舒尔算子把子图的系数矩阵分解为2个独立的矩阵:

WHL2=UWHL2SWHL2

(5)

步骤4提取水印

7) 从三角矩阵SwHL2中提取嵌入的水印，如式(6)所示：

WVsi(i)=LSB(SHL2(i,i))

(6)

步骤5视频重建

8) 通过级联从所有的帧中提取全部水印信息，构建图像水印WVsi。

9) 对所有视频场景重复相同的过程。

3 实验结果与分析

实验中主要测试本文提出的算法在受到不同攻击下的健壮性。分4个测试场景，对应的视频片段帧分别计为F1(场景1)、F2(场景2)、F3(场景3)和F4(场景4)帧。每帧大小为458×352像素。每一个场景的快照如图3所示。水印是一个二值文本信息的图像，尺寸大为256×256像素，如图4所示。

文本通过测量提取出的水印W′与原始水印W的相似程度评估算法的鲁棒性，采用式(7)的相关性指标来衡量。相关性的取值在0和1之间，0表示2个水印不相似，1表示2个水印相同。

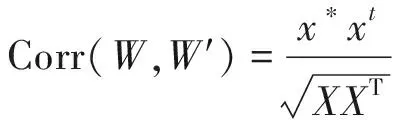
(7)

式中：x*xt表示原始水印W与提取出的水印W′像素的协方差；X与XT分别表示原始水印W与提取出的水印W′像素的方差。

图3 视频场景快照

图4 原始水印

3.1 无感知性测试

在场景1的F1视频中加入水印后的第2帧，其PSNR值为57.43 dB，与图3中的测试原始图像(未嵌入水印)相比，在视频片段中嵌入水印后没有引起可视的退化现象，如图5(a)所示；并且嵌入和提取水印间的相似性是完全相似的，如图5(b)和图5(c)所示。所有水印帧的平均PSNR值为57.31 dB。在这个PSNR值的情况下，被嵌入水印的视频没有质量退化被感知，这说明本文提出的算法具有很高的无感知性。PSNR(峰值信噪比)的定义如式8所示。

(8)

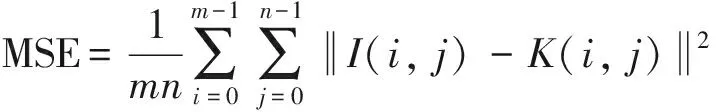
图5 标准测试中提取水印与原始水印的比较

3.2 攻击下的健壮性测试

在标准攻击和帧攻击两种情况下，对本文算法的健壮性进行测量。标准攻击包括压缩、旋转、高斯噪声、盐椒噪音等；帧攻击就是帧交换、帧平均和帧丢弃。对于这两种类型的攻击本文使用相关性来测量原始水印和被提取水印之间的相似性。

1) 盐椒噪声和高斯噪声攻击

在盐椒噪声和高斯噪声的攻击下，本文算法的健壮性是可以接受的,因为水印仍然良好并且相关性较高,与其他攻击相比，这是合理的，因为噪声添加会影响水印帧的每一像素点(结果如表1所示)。

2) 旋转攻击下的健壮性测试

对于旋转攻击，旋转水印图像分别为30°、90°和180°。本文算法对抗攻击具有很高的鲁棒性。在旋转30°时，4个场景提取的水印的相关性都为1；在旋转90°时，4个场景提取的水印的相关性都为1；在旋转180°时，4个场景的提取的水印的相关性都约为1；相关性的值很高(旋转攻击的结果略)。因此,就如前面讨论一样，S矩阵的对角被选择用于本算法的水印嵌入,这是由于在舒尔分解中，本征值是十分稳定的，并且提高了鲁棒性。

3) 视频攻击下的健壮性测试

针对视频攻击，测试水印场景的鲁棒性。首先，进行帧交换攻击测试，把每个水印场景的第4帧和10帧进行交换；其次，进行帧平均视频攻击测试；最后，进行帧丢失攻击测试，这里从水印场景中丢失了90%的帧。如表2所见，结果反映在被提取的水印中,只能看到大约10%的水印,剩下部分随着视频的丢失而丢失了。这是因为水印是分布在每个视频场景的所有帧中。

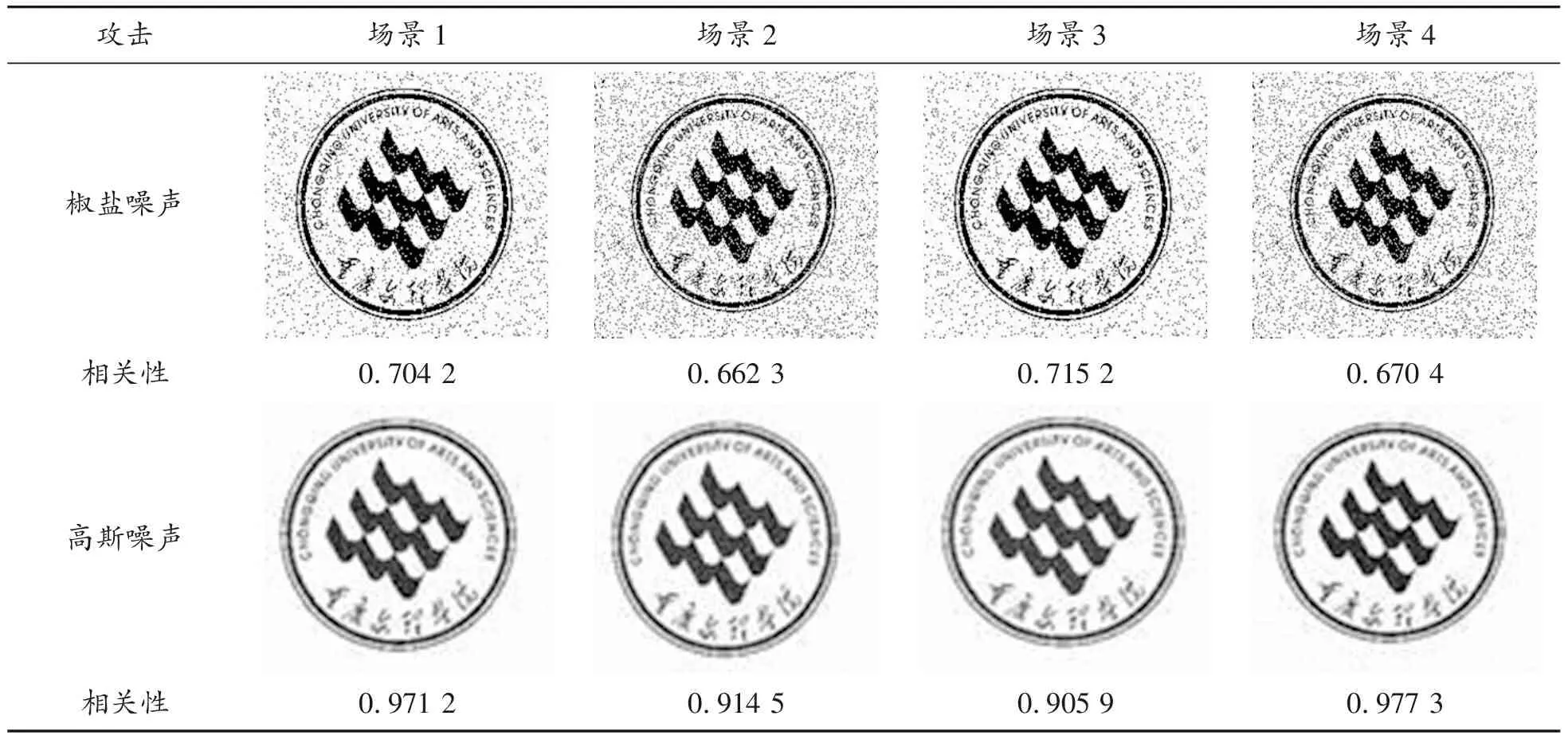
表1 噪声添加攻击后的结果

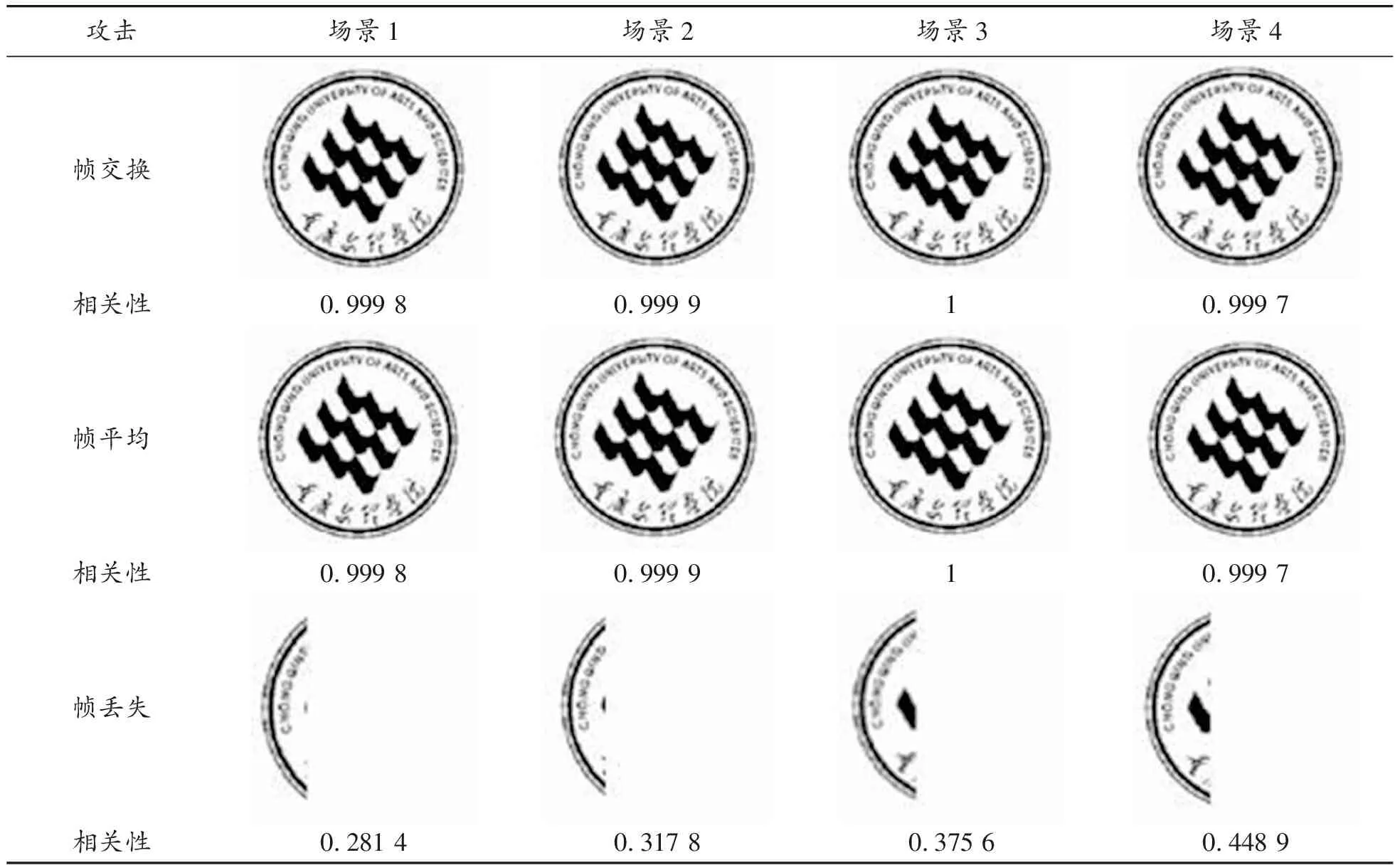
表2 视频帧攻击后的结果

4 结束语

数字水印是保护数字媒体所有权和版权的最有力的工具之一。本文提出了一种DWT-Schur结合的全盲数字视频水印算法，采用离散小波变换和舒尔分解相结合，实现了水印的嵌入与提取。采用Matlab对算法进行实现，测试了本文算法的抗标准攻击和视频攻击性能。实验结果表明：本算法具有较强的无感知性、盲特性和鲁棒性。