轮胎非线性对自主车队稳定性的影响分析*

李 玲，姚喜贵，施树明

（1.宁波工程学院机械工程学院，宁波 315336； 2.吉林大学交通学院，长春 130022）

前言

自主车队控制系统作为自动化公路系统最重要的子系统之一，旨在通过导航和控制技术使车辆以车队形式自动行驶，从而提高公路系统的运行效率和安全性。目前，自主车队系统模型可根据自主车队控制方面的研究分为纵向控制、横向控制和综合控制3种车辆模型。车辆纵向控制的研究主要集中在自适应巡航控制（ACC/CACC/CCC）、避障等方面［1-3］。车辆横向控制又称为车辆的转向控制，调查研究［4］发现，车道偏离是导致致命交通事故的首要原因，因此加强车辆的横向控制也是目前减少交通事故的重要手段。任殿波等［5］基于单点预瞄方法建立了车辆横向位置误差和横摆角误差动态模型，采用非奇异终端滑模方法设计了车道保持控制规律，并进行了控制系统稳态误差的分析。综合控制是把车辆纵向控制与横向控制进行有机的协调与结合，使被控车辆在车道上顺利完成转弯的过程中，兼顾到车辆速度的损失情况，力争使车速降幅达到最低［6］，并要求能处理紧急情况（如躲避障碍等）。Swaroop等［7］针对紧急换道运动，在3自由度非线性单轨车辆模型的基础上，设计了一个纵、横向集成控制器，即滑模控制器。仿真结果显示，该滑模控制器具有非常好的纵、横向跟随特性。但该研究所建立的车辆纵向动力学模型中没有考虑轮胎非线性特性，采用线性轮胎模型进行仿真分析，不能反映实际车辆运行中轮胎的非线性动力学特征。李玮等［8］为实现车辆安全平稳换道，建立了车辆纵、横向非线性动力学耦合模型，根据干扰观测器理论和滑模控制方法研究了车辆换道纵、横向耦合控制问题，提出了一种滑模控制与干扰观测器相结合的复合控制策略，并基于Lyapunov理论分析了该控制系统的稳定性。但该车辆模型中同样没有考虑轮胎的非线性问题。

为揭示车辆系统纵向加速度对系统稳定性的影响，Liu等［9］建立了3自由度车辆系统稳定性分析模型。研究表明，车辆系统在高速行驶中转向时，轮胎侧向力的非线性特性是导致车辆失稳的根本原因。轮胎侧偏特性决定了车辆转向动力学特征，在极限工况下，轮胎侧向力与侧偏角之间的关系表现出高度非线性，对应的车辆操纵性与线性轮胎模型有很大的差别。因此Koo等［10］指出，在极端驾驶条件下，为实现对车辆侧向稳定性的控制，通常需要准确的轮胎模型来估计车辆运动状态。沈法鹏等［11］为分析轮胎侧向力对汽车转向稳定性的影响，采用4自由度整车动力学模型及非线性轮胎侧向力模型进行了仿真研究，并通过虚拟试验和实车试验进行了验证。结果表明，基于非线性轮胎侧向力模型的仿真与试验结果较为相近，能更真实地反映各运动状态响应。为完整分析轮胎力在稳定状态和失稳状态（即线性和非线性区域内）的动力学特征，Wang等［12］对车轮转动动力学进行深入分析，并提出了统一的滑移率公式。根据Pacejka教授［13］的研究，针对车辆后退的情况，Mu等［14］对现有的轮胎侧偏角公式进行修正，扩大了其应用范围，建立了适用于轮胎混合滑移的任何工况的统一轮胎侧偏角模型。

本文中在前期工作的基础上，兼顾真实性和简洁性，将5自由度非线性车辆模型引入车队系统中，根据文献［5］和文献［16］中设计的跟随控制器输出确定弯道跟随车的控制输入。为研究轮胎非线性对车队跟随行驶稳定性的影响，分别采用线性轮胎模型和非线性轮胎模型，分析不同初始跟随车速条件下，自主车队系统的动力学特性和稳定性。

1 车辆动力学模型与轮胎模型

1.1 5自由度车辆模型

考虑到2自由度车辆模型本身的局限性，本文中在由纵向、横向和横摆组成的3自由度车辆模型的基础上，引入车轮转动动力学，采用文献［12］中建立的基于轮胎混合滑移特征的5自由度非线性车辆模型。由于本文的研究重点是车辆系统的平面运动稳定性，因此假设车辆质心位于地面上，忽略车轮之间的载荷转移，即该模型不考虑车身俯仰和侧倾的影响。采用能表达车辆在平面内的全局运动及其主要动力学特征的单轨车辆模型，车辆系统动力学模型为

式中：vx为纵向速度；vy为侧向速度；γ为横摆角速度；ωf为前轮角速度；ωr为后轮角速度；Tdf为前轮驱动力矩；Tdr为后轮驱动力矩；Tbf为前轮制动力矩；Tbr为后轮制动力矩；Fxf为前轮纵向轮胎力；Fxr为后轮纵向轮胎力；Fyf为前轮侧向轮胎力；Fyr为后轮侧向轮胎力；m为整车质量，m=1500 kg；Iz为绕z轴的转动惯量，Iz=3000 kg·m2；lf为汽车前轴到质心的距离，lf=1.2 m；lr为汽车后轴到质心的距离，lr=1.3 m；J为车轮转动惯量，J=1 kg·m2；δf为前轮转角；Cx为纵向风阻系数，Cx=0.3；Cy为侧向风阻系数，Cy=0.4；Ax为纵向迎风面积，Ax=1.7 m2；Ay为侧向迎风面积，Ay=3.5 m2；ρ为空气密度，ρ=1.2258 kg/m3；Rw为车轮转动半径，Rw=0.307 m［17-18］。

1.2 轮胎模型

为研究轮胎非线性对车队跟随行驶稳定性的影响，分别采用线性轮胎模型和非线性轮胎模型，分析自主车队系统的动力学特性及稳定性。

1.2.1 线性轮胎模型

在轮胎纵、横向滑移特性中，纵向滑移率增加时，轮胎侧向力有所减小。在附着系数为μ的路面上，若轮胎处于滚动状态时，车轮上所受到的纵向力Fx与侧向力 Fy的矢量和不应超过摩擦圆，即为垂直载荷）。若低滑移状态下滑移曲线的斜率分别为纵向刚度Cf和 侧向刚度Cr，则轮胎纵、侧向力的线性表达式为

式中：κ为轮胎滑移率；α为轮胎侧偏角。

1.2.2 非线性轮胎模型

针对轮胎的强非线性特征，研究人员建立了魔术公式模型、Unityre模型和Fiala模型等多种轮胎模型。其中 Pacejka［13，19］提出的魔术公式由于具有拟合精度高、表达方便、拟合参数少和各参数物理意义明确等优点被广泛采用。本文中采用经典的魔术公式计算轮胎力，即

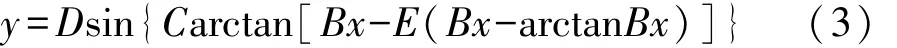
式中：x为轮胎滑移率κ或侧偏角α；y为轮胎稳态纵向力或侧向力；B，C，D，E为轮胎参数，具体参数取值见表 1［20］。

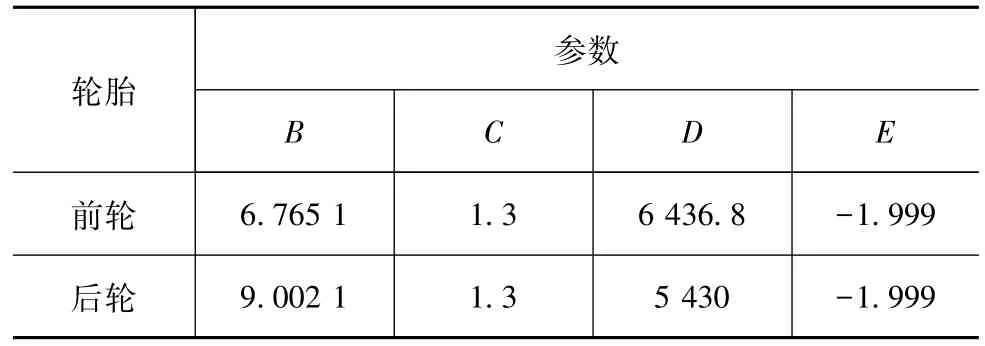
表1 轮胎参数

Pacejka教授提出的魔术公式曲线，分别表达了轮胎纵向力-滑移率和轮胎侧向力-侧偏角之间的函数关系。系数B，C，D的乘积对应于原点处的斜率，本文中假设轮胎纵、侧向刚度相同，则

汽车在驱动转向或制动转向行驶中，轮胎纵、侧向力同时存在且相互影响，即混合滑移工况，该条件下轮胎纵、侧向力计算式［13］为

式中：Fxf0，Fxr0，Fyf0，Fyr0分别为前后轮稳态轮胎纵、侧向力；δr为后轮转角，δr=0；Gx，Gy分别为轮胎混合滑移修正函数；Bg，x，Bg，y分别为轮胎滑移形状函数；rx，1，rx，2，ry，1，ry，2为轮胎混合滑移系数，rx，1=35，rx，2=40，ry，1=40，ry，2=35。

本文中分别采用适用于全工况的式（6）轮胎滑移率模型［12，21］和式（7）轮胎侧偏角模型［14］计算轮胎纵、侧向力。

式中：ωw为轮胎转动角速度；vwx为轮心纵向速度；αf，αr分别为前后轮侧偏角；vxf，vyf，vxr，vyr分别为轮胎坐标系下前后轮纵、侧向速度。

2 前车与跟随车的控制输入

本文中车辆系统的控制输入分别为前后轮转角和驱动/制动力矩，其中前车的转角和力矩由驾驶员控制输入，跟随车的转角和力矩则通过跟随控制器控制输入。

2.1 前车车辆系统控制参数输入

试验路径信息为

道路曲率为

根据式（8）和式（9）计算得到试验路径曲率近似表示为

将道路曲率半径表达式R=1/ρ1和汽车纵向位移表达式X=vxi-1t代入式（10），可确定前车（称i-1车）前后轮转角输入为

式中：X为绝对坐标系下汽车纵向位移；Ylat为汽车侧向位移；ρ1为道路曲率；Li-1为前车车身长度；vxi-1为前车纵向速度；δfi-1为前车前轮转角；δri-1为前车后轮转角。

假设前车始终匀速行驶，在车辆系统动力学模型中只考虑了风阻的作用，因此，前车驱动力矩大小按照车身受到的空气阻力来计算。由于大转角下轮胎侧向力明显增加，轮胎纵向力所占比例减小，为保证车辆系统在大转角下匀速行驶，考虑取空气阻力计算结果的κ1倍，因此，前车驱动力矩为

式中：Tdi-1为前车驱动力矩；vyi-1为前车侧向速度。

文中车辆系统均采用单轨车辆模型，根据力矩分配的要求［22］，采用的力矩分配方式为：在驱动条件下前后轴为等矩分配，在制动条件下前后轴制动力矩分配比为0.6∶0.4。

2.2 跟随车辆系统控制参数输入

跟随控制器在纵向上控制输出的加速度ui为

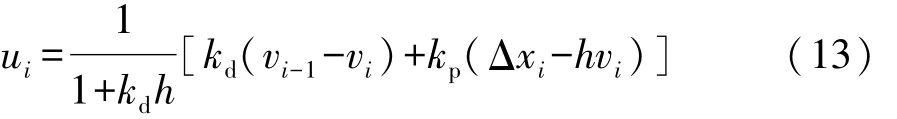
保证纵向控制系统稳定的控制参数值为kp=1，kd=1.5，其中前后轴力矩分配方式与前车一致，确定跟随车车辆系统的力矩输入为

式中：vi-1为i-1车车速；vi为 i车车速；h为固定时距；Δxi为两车实际纵向间距；Tdi为i车驱动力矩；mi为i车整车质量；Rwi为i车车轮转动半径。

弯道行驶中同时考虑前后两车的侧向距离差和方位差，采用郭孔辉［23］的点斜预瞄模型（PO模型）确定跟随车前轮转角输入。在不考虑车辆的运动惯性条件下取λ=1，跟随车期望侧向加速度为

根据式（15）和Acklman几何关系，可得到跟随车最优前轮转角和后轮转角的表达式［15］为

式中：yi为车辆坐标系下汽车侧向位移；T为前视时间；Δyi为两车实际侧向间距；vyi为i车侧向速度；di为前视距离；Li为i车车身长度；δfi为i车前轮转角；δri为 i车后轮转角。

3 仿真分析

车队跟随行驶中车辆加速跟随前车、减速离开车队等操作都会引起前后车速波动，因此，根据前后车速度差不同确定跟随车车速。跟随行驶中3辆跟随车的初始状态相同，分别在两种不同的初始跟随车速条件下，采用线性轮胎模型和非线性轮胎模型，分析自主车队系统的动力学特性和稳定性。取放大倍数 κ1=2，前后车速差Δvx=5 m/s，vyi-1=0，ωi-1=0，vyi=vyi+1=vyi+2=0，ωi=ωi+1=ωi+2=0，初始车距均为2 m。两种不同初始跟随车速条件分别为：（1）前车纵向速度vxi-1=17 m/s匀速行驶，跟随车纵向速度vxi=vxi+1=vxi+2=12 m/s，固定时距 h=0.15 s；（2）前车纵向速度vxi-1=30 m/s，匀速行驶，跟随车纵向速度vxi=vxi+1=vxi+2=25 m/s，固定时距h=0.08 s。车间时距的选取是保证跟随行驶中车间距接近2 m，仿真时间20 s，分析车辆系统的跟随特征。

3.1 基于线性轮胎模型的车队系统仿真分析

图1～图4分别为前车vxi-1=17 m/s匀速行驶，跟随车vxi=vxi+1=vxi+2=12 m/s，固定时距h=0.15 s时仿真时间20 s内，前后车速度相平面轨迹、状态变量、质心运动轨迹和纵侧向距离偏差的变化情况。

图1中跟随车相平面图表明，自主车队在跟随行驶过程中，3辆跟随车运动状态稳定。系统状态变量（图2）仿真结果显示，i-1车纵向速度保持匀速，侧向速度和横摆角速度由初值开始稳定地周期振荡。3辆跟随车在跟随控制器作用下，保持与其前车基本一致的状态行驶。

图1 线性轮胎模型前后车速度相平面轨迹（前车速度为17 m/s时）

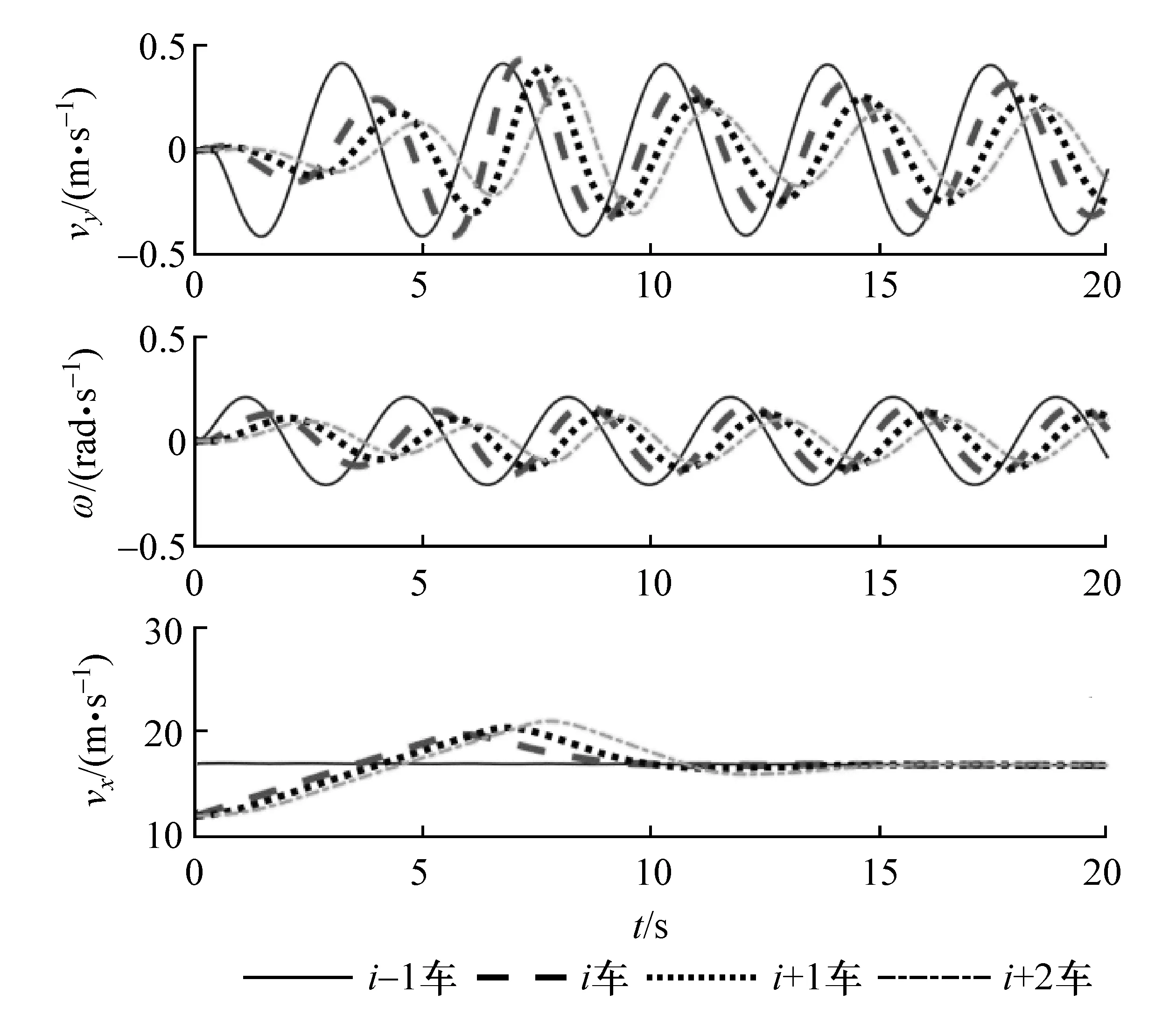
图2 线性轮胎模型前后车状态变量（前车速度为17 m/s时）

图3 线性轮胎模型前后车质心运动轨迹（前车速度为17 m/s时）

图4 线性轮胎模型前后车纵侧向距离偏差（前车速度为17 m/s时）

图3 中显示，在跟随行驶过程中前后车均能保持正常的正弦路线行驶，对应的前后车间的纵、侧向距离偏差（图4）显示，在经过14 s的跟随控制器调节后，前后车纵向间距偏差稳定到零值，对应的纵向车间距均接近 2 m；侧向间距偏差在［-0.1 m，0.1 m］范围内波动，对应的侧向车间距均接近零；跟随车与其前车运动轨迹基本吻合。因此，该条件下的仿真结果表明，在跟随控制器调节作用下，3辆跟随车能很好地实现正弦路径下的稳定跟随。

图5～图7分别为前车vxi-1=30 m/s匀速行驶，跟随车vxi=vxi+1=vxi+2=25 m/s，固定时距h=0.08 s时仿真时间20 s内，前后车速度相平面图、状态变量、质心运动轨迹。图8为对应于图7的跟随车与其前车的纵、侧向距离偏差的仿真结果。

图5 线性轮胎模型前后车速度相平面轨迹（前车速度为25 m/s时）

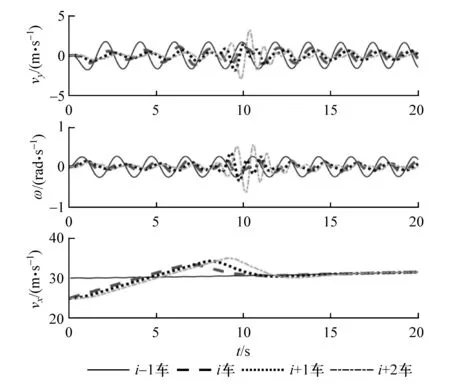
图6 线性轮胎模型前后车状态变量（前车速度为25 m/s时）

图7 线性轮胎模型前后车质心运动轨迹（前车速度为25 m/s时）

图8 非线性轮胎模型前后车纵侧向距离偏差（前车速度为17 m/s时）

从图5看出，跟随控制器调节过程中跟随行驶的i+2车相轨迹出现扰动。从图6看出，在控制器跟随调节过程中，车辆系统出现小的扰动，但该扰动并不明显，整个仿真过程中，跟随车能稳定跟随前车行驶。

图7和图8的仿真结果与图3和图4相似，在跟随行驶过程中，前后车均能够保持正常的正弦路线。由图8可见，在经过15 s的跟随控制器调节后，前后车纵向间距偏差稳定到零值，对应的纵向车间距均为2 m。侧向间距偏差在［-0.5 m，0.4 m］范围内波动，对应的侧向车间距均接近零，跟随车与其前车运动轨迹基本吻合。因此，该条件下的仿真结果表明，采用线性轮胎模型的自主车队系统，在高速条件下仍能很好地实现正弦路径下多车稳定跟随。

3.2 基于非线性轮胎模型的车队系统仿真

图9～图11分别为前车vxi-1=17 m/s匀速行驶，跟随车vxi=vxi+1=vxi+2=12 m/s，固定时距h=0.15 s时仿真时间20 s内，前后车速度相平面轨迹、状态变量和质心运动轨迹。图12为对应于图11的前后车纵侧向距离偏差的变化情况。

图9 非线性轮胎模型前后车速度相平面（前车速度为17 m/s时）

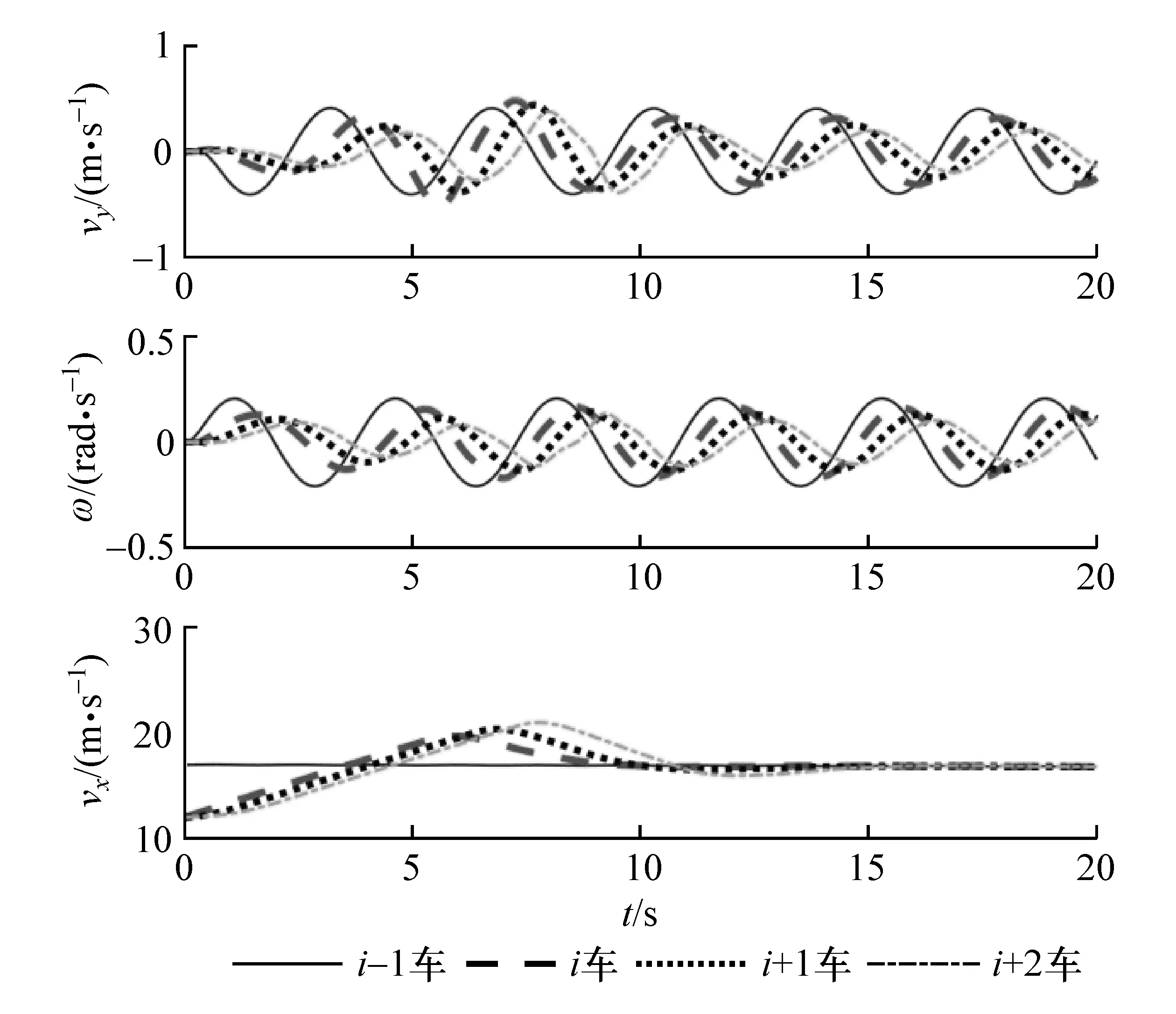
图10 非线性轮胎模型前后车状态变量（前车速度为17 m/s时）

从图9可以看出，前车相轨迹与图1中的结果一致，前后车相轨迹规则变化。从图10可以看出，在经历跟随控制器的初始调节过程后，3辆跟随车能够保持与前车一致的运动状态稳定跟随行驶。

由图11可见，整个仿真过程中前后车均能保持正常的正弦路线行驶，而由图12可见，在经过14 s的跟随控制器调节后，前后车纵向间距偏差稳定到零值，对应的纵向车间距均接近2 m；侧向间距偏差在［-0.2 m，0.2 m］范围内波动，与采用线性轮胎模型时的结果相比，波动范围明显增大，但对应的侧向车间距仍均接近零；跟随车与其前车运动轨迹基本吻合。因此，该条件下的仿真结果表明，3辆跟随车能够很好地实现正弦路径下的稳定跟随。

图11 非线性轮胎模型前后车质心运动轨迹（前车速度为17 m/s时）

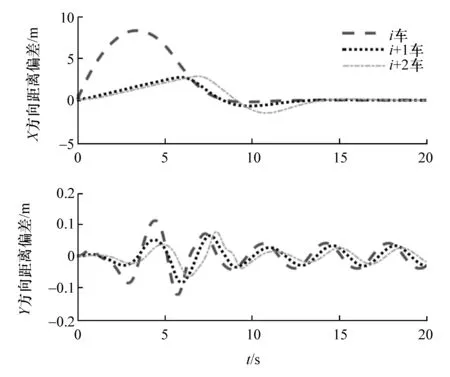
图12 非线性轮胎模型前后车纵侧向跟随偏差（前车速度为17 m/s时）

图13 ～图15为前车vxi-1=30 m/s匀速行驶，跟随车vxi=vxi+1=vxi+2=25 m/s，固定时距h=0.08 s时仿真时间20 s内，前后车侧向速度与横摆角速度相平面、状态变量和质心运动轨迹。图16为对应于图15的跟随车与其前车的纵侧向距离偏差的仿真结果。

从图13可以看出，跟随控制器调节过程中跟随行驶的i+2车相轨迹出现不规则变化。从图14可以看出，在跟随行驶过程中，i+2车侧向速度在［-30 m/s，30 m/s］范围波动，横摆角速度变化范围为［-3 rad/s，2 rad/s］，纵向速度在［-20 m/s，35 m/s］范围内变化，表征i+2车出现失稳运动。

图13 非线性轮胎模型前后车速度相平面（前车速度为25 m/s时）

图14 非线性轮胎模型前后车状态变量（前车速度为25 m/s时）

图15 和图16的仿真结果与线性条件下的仿真结果差别较大。从图15可以看出，跟随行驶过程中i车和i+1车均能保持与前车一致的正弦路线行驶，而i+2车则在跟随行驶一段时间后迅速偏离其前车行驶路径。从图16可以看出，经过跟随控制器的调节后，i车和i+1车与其前车纵向间距偏差稳定到零值，对应的纵向车间距均接近2 m；侧向间距偏差在零附近波动，对应的侧向车间距均接近零；跟随车与其前车运动轨迹基本吻合。i+2车由于出现失稳运动而与其前车纵、侧向间距偏差在很大范围内变化。

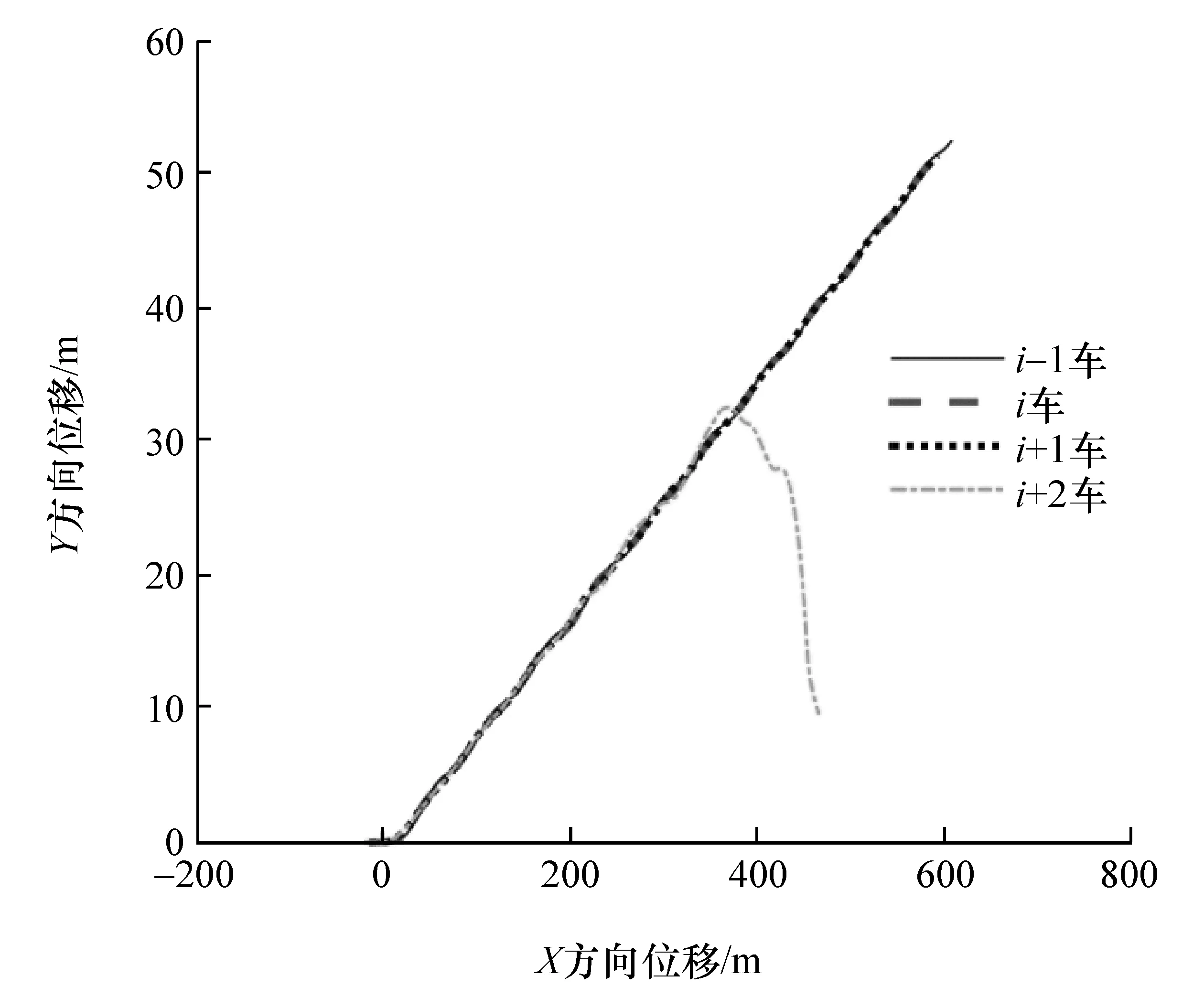
图15 非线性轮胎模型前后车质心运动轨迹（前车速度为25 m/s时）

图16 非线性轮胎模型前后车纵侧向跟随偏差及其局部放大（前车速度为25 m/s时）

上述基于线性和非线性轮胎模型的车队系统仿真结果显示，在前车vxi-1=17 m/s匀速行驶，跟随车vxi=vxi+1=vxi+2=12 m/s，固定时距 h=0.15 s时，两种轮胎模型条件下，车队系统的仿真结果类似，3辆跟随车均能够在跟随控制器的作用下稳定地跟随其前车行驶。在前车vxi-1=30 m/s匀速行驶，跟随车vxi=vxi+1=vxi+2=25 m/s，固定时距h=0.08 s时，两种轮胎模型条件下，车队系统的仿真结果差别较大：基于线性轮胎模型的车队系统仿真结果表明，3辆跟随车在前车速度较高时仍能稳定地跟随前车行驶；但基于非线性轮胎模型的车队系统仿真结果显示，跟随车i和i+1仍能稳定地跟随前车行驶，但跟随车i+2在跟随行驶过程中出现失稳运动。

4 结论

基于前期研究工作，利用有效性得以验证的5自由度车辆模型和弯道行驶跟随控制器，分别采用线性轮胎模型和非线性轮胎模型，在不同初始跟随车速条件下，分析自主车队系统的动力学特性和稳定性。结果表明，低速跟随行驶时，轮胎非线性对跟随行驶车辆的稳定性影响不显著，3辆跟随车均稳定跟随行驶。但高速跟随行驶中轮胎的非线性会引发跟随行驶后车（i+2车）的失稳运动。