SMA压电复合减震装置电力学性能及其本构模型*

展 猛， 王社良， 赵 云

(1.黄淮学院建筑工程学院 驻马店，463000) (2.西安建筑科技大学土木工程学院 西安，710055) (3.天津大学建筑工程学院 天津，300000)

引 言

形状记忆合金是一种应用较为广泛的智能材料，利用其相变伪弹性设计成的SMA阻尼器已被广泛用于土木工程结构的被动耗能减震控制中[1-2]。由于不能实时调整控制力，限制了其在结构振动控制中的应用。压电陶瓷是一种具有瞬间电致变形特性的功能材料，其与摩擦阻尼器结合制成的压电摩擦阻尼器是土木工程结构控制常见的一种耗能减震装置[3-4]。但是，压电摩擦阻尼器一般都需要施加较大的初始压力来约束压电驱动器的变形，其半主动可调控制力有限；而预压力较小的话，出力也较小，大震中可能由于耗能不足而起不到有效地减震作用。将SMA材料与压电材料制成复合型减震装置可以实现优势互补，对工程结构全过程起到有效减震控制，但研究处于探索阶段，相关研究成果较少。王社良等[5]前期利用改进的遗传算法，对设计的SMA压电复合阻尼器在空间杆系结构中的优化配置进行了分析。Dai等[6]将研发的SMA压电复合减震装置应用于钢框架模型的基础隔震，进行了振动台试验研究。Ozbulut等[7]采用模糊控制算法对20层非线性基准结构进行了SMA压电复合减震控制分析。

目前，SMA复合型减震装置的本构模型大都采用“SMA数学模型+其他”的形式。例如，钱辉等[8]设计的SMA摩擦复合阻尼器，SMA单元应力采用Graesser & Cozzarelli模型，摩擦耗能单元采用Bouc-Wen模型。卞晓芳等[9]设计的SMA-磁流变(magneto-rheological，简称MR)复合型阻尼器，SMA单元采用Graesser模型，MR阻尼力采用Bingham模型。这些SMA复合型减震装置的本构模型大都将SMA和其他单元割裂开，采用传统的数学模型，不但公式繁琐复杂、难以在Matlab程序中直接调用，而且精度很难保证。人工神经网络是一种非线性的建模方法，该方法无需预知材料的本构形式，只需考虑影响因素和预期的目标，避免了传统建模方法中的误差。目前，关于SMA神经网络本构已有一些研究。崔迪等[10]采用BP网络分别预测了加载段和卸载段不同应变幅值的SMA的应力-应变曲线，虽然分段预测的结果精度较高，但实际应用中需将加载段和卸载段合并成完整的受力过程，此时的预测精度将难以保证。任文杰等[11]以循环次数、加卸载信息和应变值作为神经元输入，采用径向基函数(radial basis function，简称RBF)网络预测了同一应变幅值的应力-应变曲线，该模型虽输入参数少、便于应用，但对应变幅值在卸载的初始段无法准确预测。文献[12]考虑加载速率和加载历史等因素，建立了SMA的遗传算法优化BP网络模型，较好地预测了不同应变幅值在卸载初始段的应力-应变曲线，但该模型神经元输入参数较多，增加了结构减震分析计算中的编程难度。神经网络本构模型虽然有一定预测精度，但神经元初始权/阈值的变化对人工神经网络的结果影响较大，因此建立神经网络本构模型中应对其初始权/阈值进行优化，以提高本构模型的精度和稳定性。

笔者结合SMA材料和压电驱动器的物理力学性能特点，提出了一种SMA单元和压电摩擦单元依次工作的复合减震装置，进行了相应的电力学性能试验。在试验结果的基础上，以速率的符号来判断加卸载的方向，建立了以速率符号、电压和位移为神经元输入的复合减震装置BP神经网络模型，并利用人工免疫算法对BP网络模型的权/阈值进行了优化。

1 SMA压电复合减震装置

1.1 构造设计

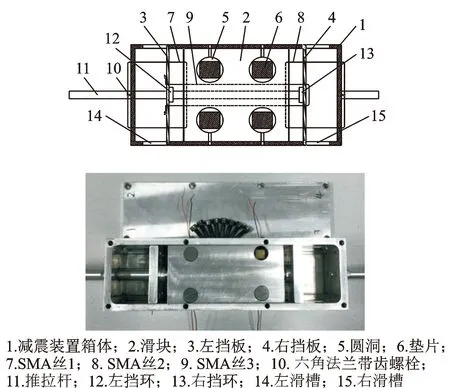
图1 SMA-压电复合减震装置示意图Fig.1 SMA-piezoelectric composite vibration damper

如图1所示，SMA压电复合减震装置主要由箱体、滑块、挡板、挡环、SMA丝和可拆卸推拉杆等组成。滑块上有4个装有压电陶瓷驱动器的圆孔，上下各有一垫片，压电驱动器的电线穿过圆洞和减震装置箱体侧壁的小圆孔与外接电源连接。SMA丝由复位丝(SMA丝1,2)和耗能丝(SMA丝3)组成，复位丝同时兼具耗能功能，每根SMA丝的两端均由六角法兰带齿螺栓固定在同一侧，以便减少接头。推拉杆在两档中间位置断开分成两部分，并通过螺丝旋转拧紧，便于安装。挡板可以在滑槽内左右滑动，同时用来固定SMA丝3。该复合装置的SMA和压电摩擦单元依次工作，当发生小的振动时，SMA单独工作；当发生大的振动时，SMA先工作，然后SMA和压电摩擦单元同时工作，且可以实时调节控制力。

当推拉杆向左运动时，左挡环推着左挡板向左移动，SMA丝3受拉耗能；当右挡环运动至滑块右端时，滑块和左挡板开始一起向左运动，此时SMA丝2，3和压电陶瓷驱动器同时耗能。当推拉杆向右运动时，右挡环顶住右挡板向右侧运动，SMA丝3受拉耗能；当左挡环运动至滑块左端时，滑块和右挡板开始一起向右运动，此时SMA丝1，3和压电陶瓷驱动器同时耗能。

1.2 性能试验

1.2.1 加载方案

考虑到SMA压电复合减震装置试验模型的尺寸以及 SMA 丝在减震装置中的固定，本次试验所用SMA丝直径为0.7 mm，化学成分为Ti-51%atNi。相变温度：Mf为-42℃，Ms为-38℃，As为-6℃，Af为-2℃，该丝在常温状态下处于奥氏体状态。在复合减震装置试验之前，首先对奥氏体SMA丝进行力学试验，以确保SMA丝的性能满足复合装置的耗能要求。鉴于目前单纯SMA丝试验研究较多，这里就不在赘述，仅给出复合装置的电力学试验。各项材料具体参数：SMA丝的最大应变幅值按7%计算，SMA丝3的数量为2根，长度为175 mm，单独工作位移为5 mm，最大伸长量为12 mm；SMA丝1，2卸载时其力比较小且行程较短，为保证复位效果，数量取为4根，长度取为100 mm，最大伸长量为7 mm；压电陶瓷驱动器是苏州攀特电陶科技股份有限公司研制的型号为PTJ1501010301的矩形压电陶瓷驱动器，各项性能指标如表1所示。

表1 矩形压电陶瓷驱动器主要性能指标

Tab.1 Performance indicators of piezoelectric actuator

参数指标数值型号PTJ1501010301外形尺寸(A×B×H)/mm10×10×36标称位移/μm400位移推力/N3 600刚度/ (N·μm-1)90最大预压力/N2 000压电应变系数d33/(10-12C·N-1)≥650

该试验在某动静材料试验机上进行，试验采用位移控制，三角波加卸载。大量研究证明，频率对SMA丝和压电智能阻尼器力学性能影响很小[13-14]，这里激励频率取0.05，0.1，0.2和0.3 Hz，加载幅值分别为5 mm(SMA丝3单独工作)、9 mm和12 mm。激励电压分别为0，40，80和120 V。试验前，复合装置在频率为0.1 Hz，电压为0，最大位移为12 mm 处拉压循环30次，以保证SMA 丝的力学性能达到稳定。试验时每个工况拉压循环2圈。试验装置如图2所示。

图2 试验装置Fig.2 Test apparatus

1.2.2 试验结果

图3为不同频率时SMA丝3单独工作时的控制力-位移曲线。限于篇幅，图4仅给出了施加40 V和80 V电压下不同频率的输出力-位移曲线。可以看出，该复合减震装置可以双向受力，滞回曲线饱满且基本对称，耗能能力较好、性能稳定，加载频率对减震装置的性能几乎没有影响。

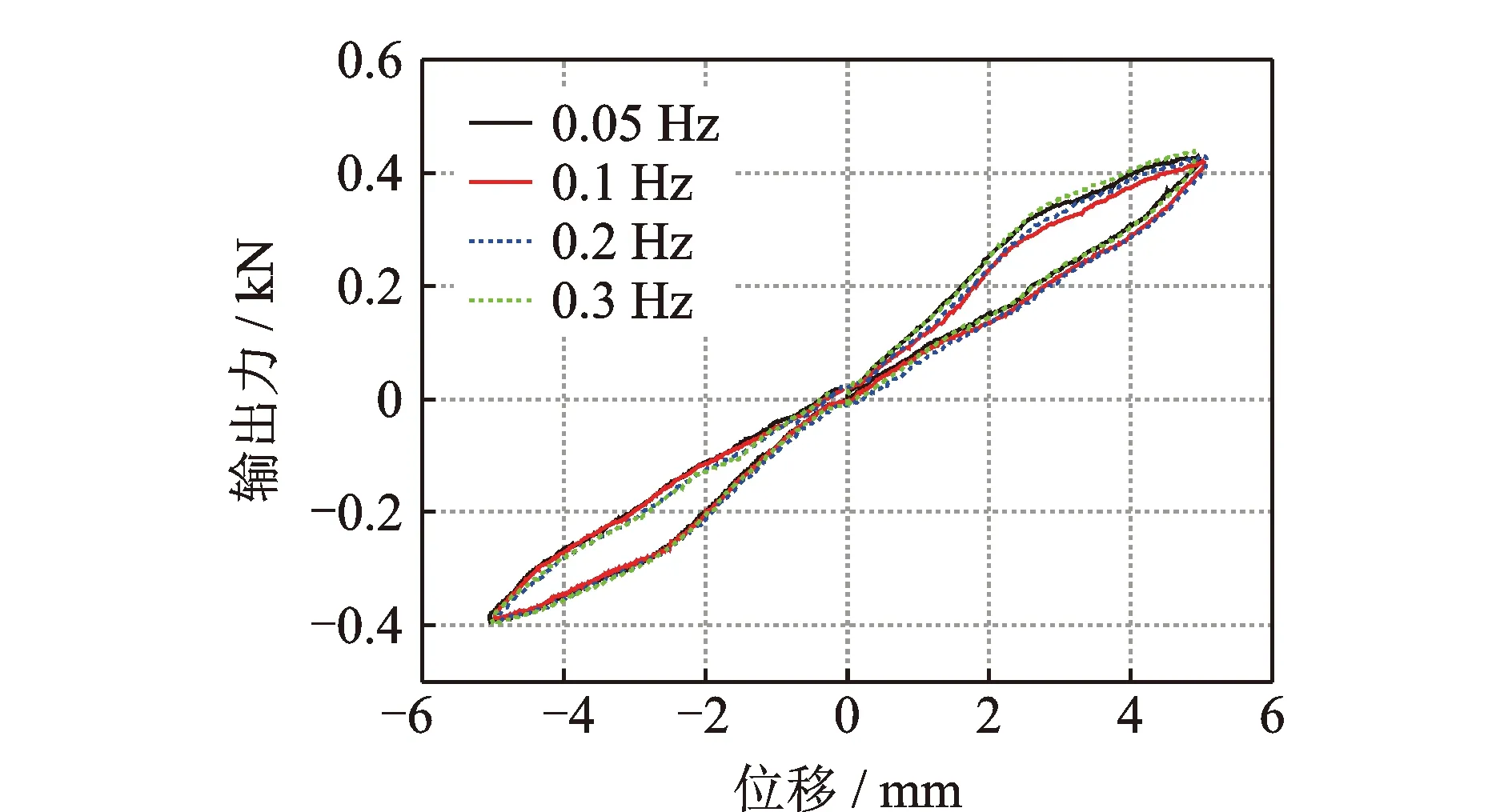
图3 SMA丝3单独工作时的输出力-位移曲线Fig.3 The output force-displacement curves when SMA wire 3 alone works

图4 不同频率下的输出力-位移曲线Fig.4 The output force-displacement curves under different frequencies

鉴于频率对试验结果影响较小，这里仅给出0.1 Hz下不同电压的控制力位移曲线，如图5所示。可以看出，当位移幅值大于5 mm时，由于复位丝和初始摩擦力的介入，控制力显著增大；且随着电压的增大，滞回环的面积逐渐增大，耗能能力不断增强。由于预紧螺栓为点固定，不能使摩擦面上的摩擦力绝对均匀，因此滞回曲线并非完全对称，这里取其绝对平均值作为最大控制力，如表2所示。图6为不同位移幅值时各工况对应的最大输出力曲线。可以看出，压电陶瓷驱动器提供的控制力与输入电压值近似呈线性关系。

压电陶瓷驱动器提供的控制力并不能直观反映其对复合减震装置耗能能力的贡献，为了分析施加电压下SMA压电复合减震装置的力学性能，现定义以下指标。

1) 单圈循环耗能Wd为一次拉压循环滞回曲线包围的面积，表示复合减震装置每个循环的耗能能力。耗能提高率α为施加电压后减震装置耗能量的提高率，表达式为

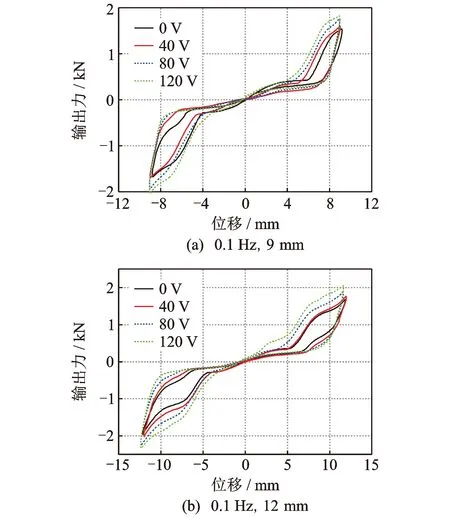
图5 不同电压时的输出力-位移曲线Fig.5 The output force-displacement curves under different voltages

表2 不同电压下的平均最大控制力

Tab.2 The average maximum control force under different voltages

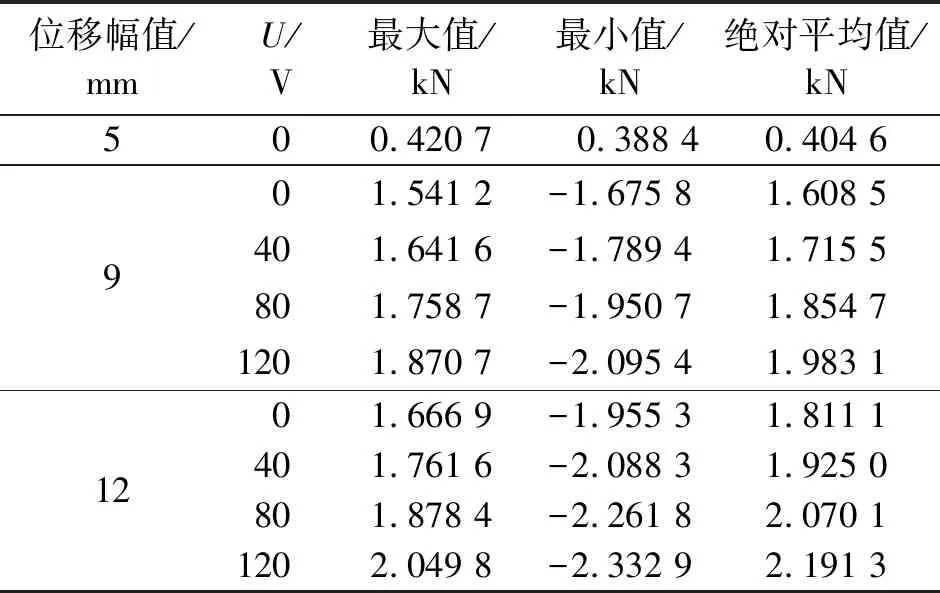
位移幅值/mmU/V最大值/kN最小值/kN绝对平均值/kN500.420 7 0.388 40.404 6901.541 2-1.675 81.608 5401.641 6-1.789 41.715 5801.758 7-1.950 71.854 71201.870 7-2.095 41.983 11201.666 9-1.955 31.811 1401.761 6-2.088 31.925 0801.878 4-2.261 82.070 11202.049 8-2.332 92.191 3

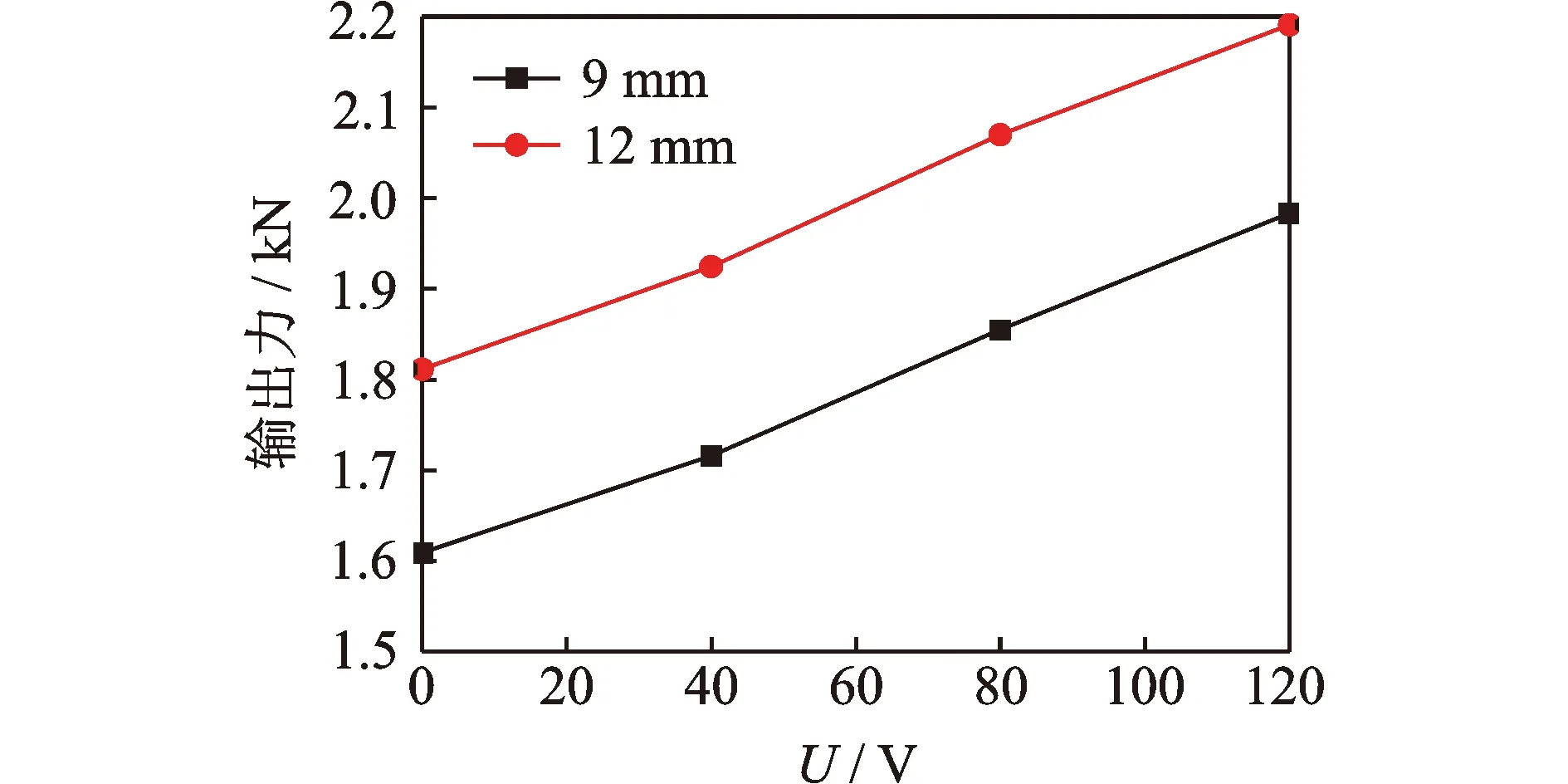
图6 不同电压时的最大输出力曲线Fig.6 The maximum output force curves under different input voltages

α=(WdU-Wd0)/Wd0

(1)

其中：Wd0为0 V所对应的单圈循环耗能；WdU为除0 V外，其他电压下的单圈循环耗能。

2) 单圈循环的等效割线刚度Ks的表达式为

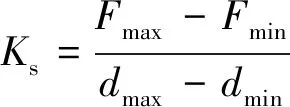
(2)

其中：Fmax，Fmin为单圈循环中的最大和最小控制力；dmax，dmin为单圈循环中的最大和最小位移。

3) 单圈循环的等效阻尼比ζa表示SMA压电复合减震装置的阻尼能力，表达式为

(3)

其中：d为一次拉压循环中位移幅值。

SMA压电复合减震装置的各项力学性能指标如表3所示。图7为不同电压时的单圈耗能曲线。可以看出，同一位移幅值下，随着电压的增加，耗能量逐渐增大，相邻电压间的耗能增量不断增大；相比位移幅值9 mm下，12 mm时的耗能量随电压增加的更快，且同一电压下的耗能增量随电压增加不断增大。这主要是因为随着电压或位移幅值的增大，滞回环的面积增大，在增加相同的控制力时，滞回环增加的面积也越大。电压从0 V增加到120 V，位移幅值为9 mm时单圈耗能量提高了83.34%，位移幅值为12 mm时单圈耗能量提高了138.23%。压电陶瓷驱动器提供的半主动控制力在数值上看起来虽然并不大，但对SMA压电复合减震装置的耗能能力却提高较多。

表3 SMA压电复合减震装置的力学性能指标

Tab. 3 Mechanical performance indicators of composite vibration damper

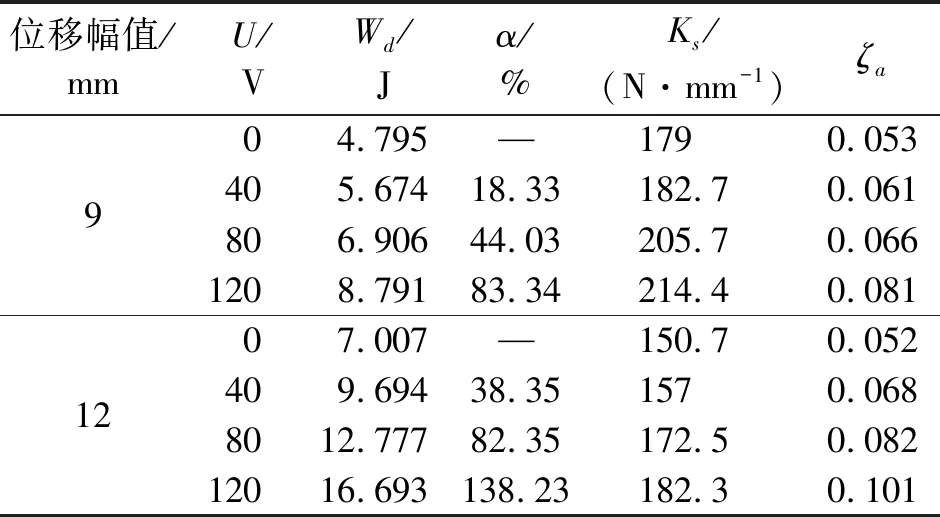
位移幅值/mmU/VWd/Jα/%Ks/(N·mm-1)ζa904.795—1790.053405.67418.33182.70.061806.90644.03205.70.0661208.79183.34214.40.0811207.007—150.70.052409.69438.351570.0688012.77782.35172.50.08212016.693138.23182.30.101

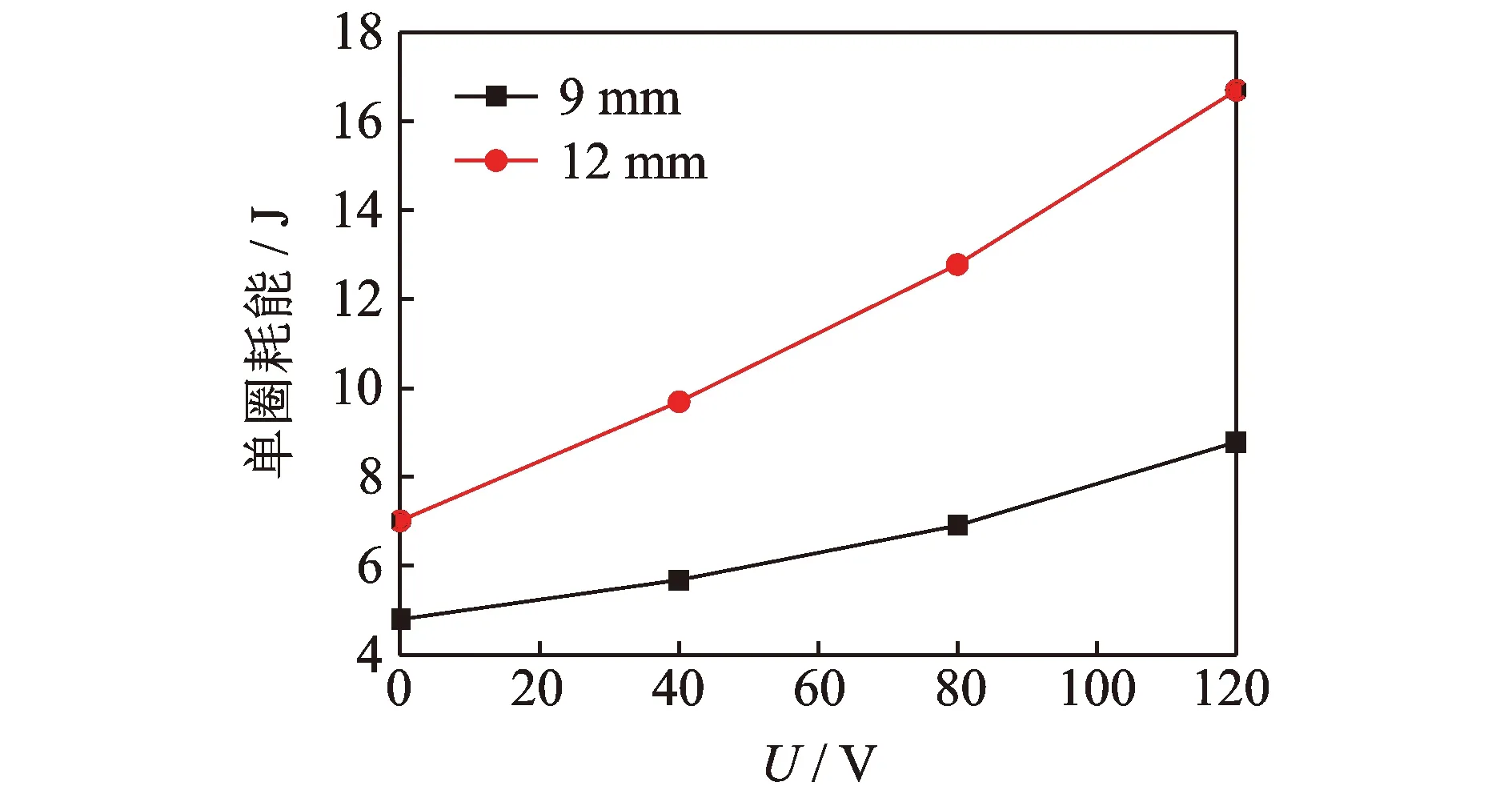
图7 不同电压时的单圈耗能值Fig.7 Lap value of energy consumption under different input voltages

图8为等效割线刚度和等效阻尼比随输入电压的变化曲线。同一位移幅值下，随着电压的增加，等效割线刚度和等效阻尼比都不断增大。电压从0 V增加到120 V时，位移幅值9 mm时的等效割线刚度提高了19.78%，等效阻尼比提高了52.83%；位移幅值12 mm时的等效割线刚度提高了20.97%，等效阻尼比提高了94.23%。随着位移幅值增大，等效割线刚度减小，等效阻尼比增大，耗能能力增强。随着电压的增大，不同位移幅值的等效割线刚度的增量变化较小，而此时的单圈耗能增量增大(图7)，因此等效阻尼比的增量也逐渐增大。

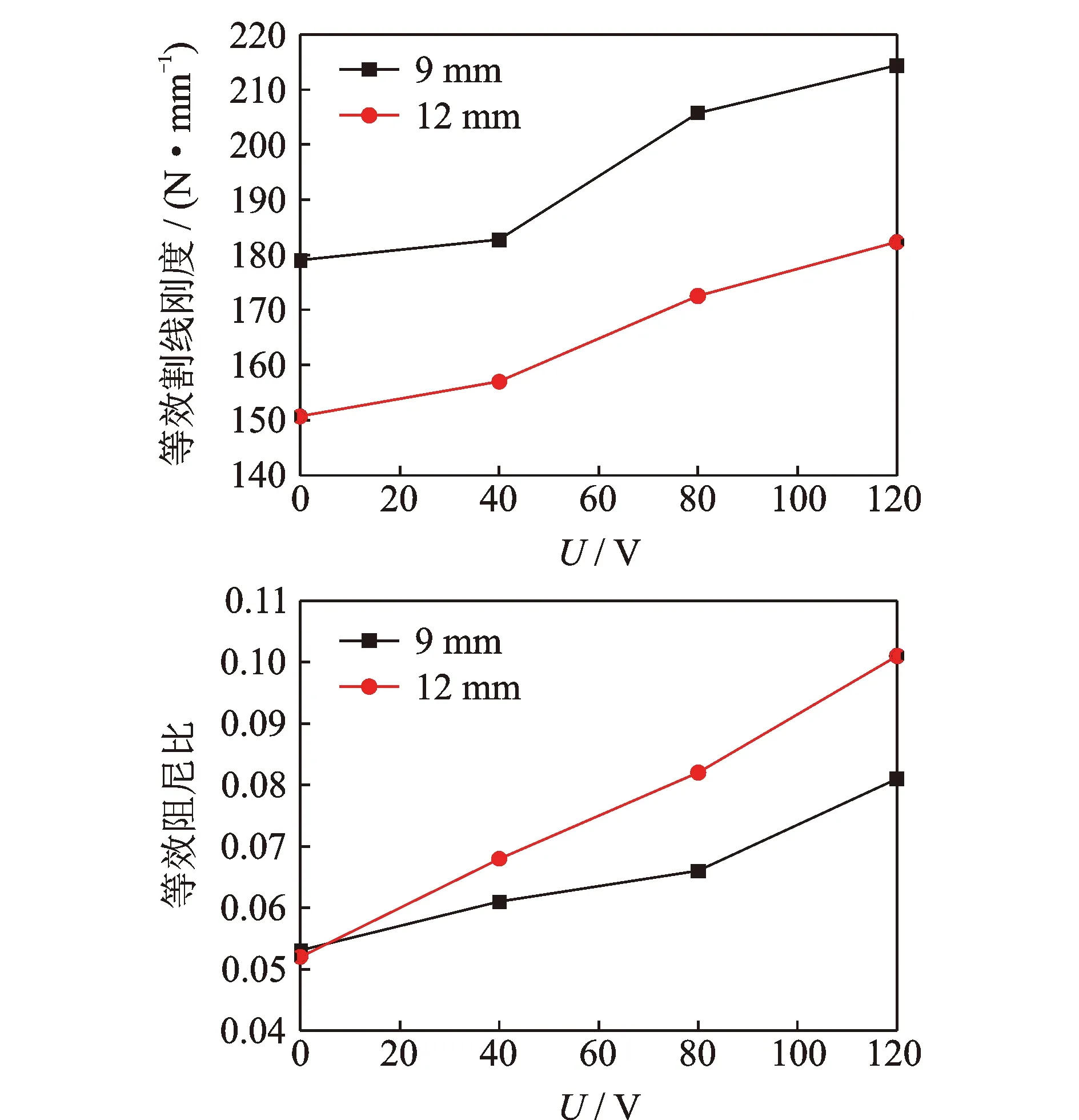
图8 等效割线刚度和等效阻尼比随电压变化曲线Fig.8 Equivalent secant stiffness and damping ratio curves under different voltage

2 复合减震装置神经网络本构模型

2.1 网络结构

以速率的符号来判断加卸载的方向，同时考虑施加电压的影响，建立3层BP神经网络模型来预测SMA压电复合减震装置的输出力。由于频率对试验结果影响较小，且没有呈现明显的规律性，因此SMA压电复合减震装置神经网络本构模型不再考虑频率因素，其神经元输入为电压、位移和速率符号，隐层通过估算法确定[15]，取10个，神经元输出为控制力，拓扑结构为3-10-1。

2.2 样本数据

由于SMA压电复合减震装置试验工况较少，施加电压的位移幅值只有2个，且每个工况仅循环了2圈，可以把不同频率的试验数据看成圈数，以增加样本数量，同时不再预测不同位移幅值的输出力-位移曲线，仅考虑不同电压下的本构曲线预测。试验工况共有8个，选取其中2组作为检验数据，分别为：a.位移幅值为9 mm、电压为80 V；b.位移幅值为12 mm、电压为80 V。其余6种工况为训练样本。

2.3 优化参数

未经优化BP网络的初始权/阈值由系统随机分配；而经优化BP网络的初始权/阈值由人工免疫算法[16]寻优确定。由BP网路的结构可知，BP网络待确定的权值有3×10+10×1=40个，待确定的阈值有10+1=11个，因此优化算法的变量为所有权值和阈值，变量总数为51个。采用实值编码，染色体长度为51，目标函数取训练样本经BP网络预测所得的期望输出与实际输出的误差平方和。人工免疫算法的其他参数设置如下：初始抗体种群为10，克隆规模为10，变异概率为0.005，一般抗体单元概率阈值取0.1，记忆单元概率阈值取0.01，记忆单元个体数量为5。

2.4 仿真结果

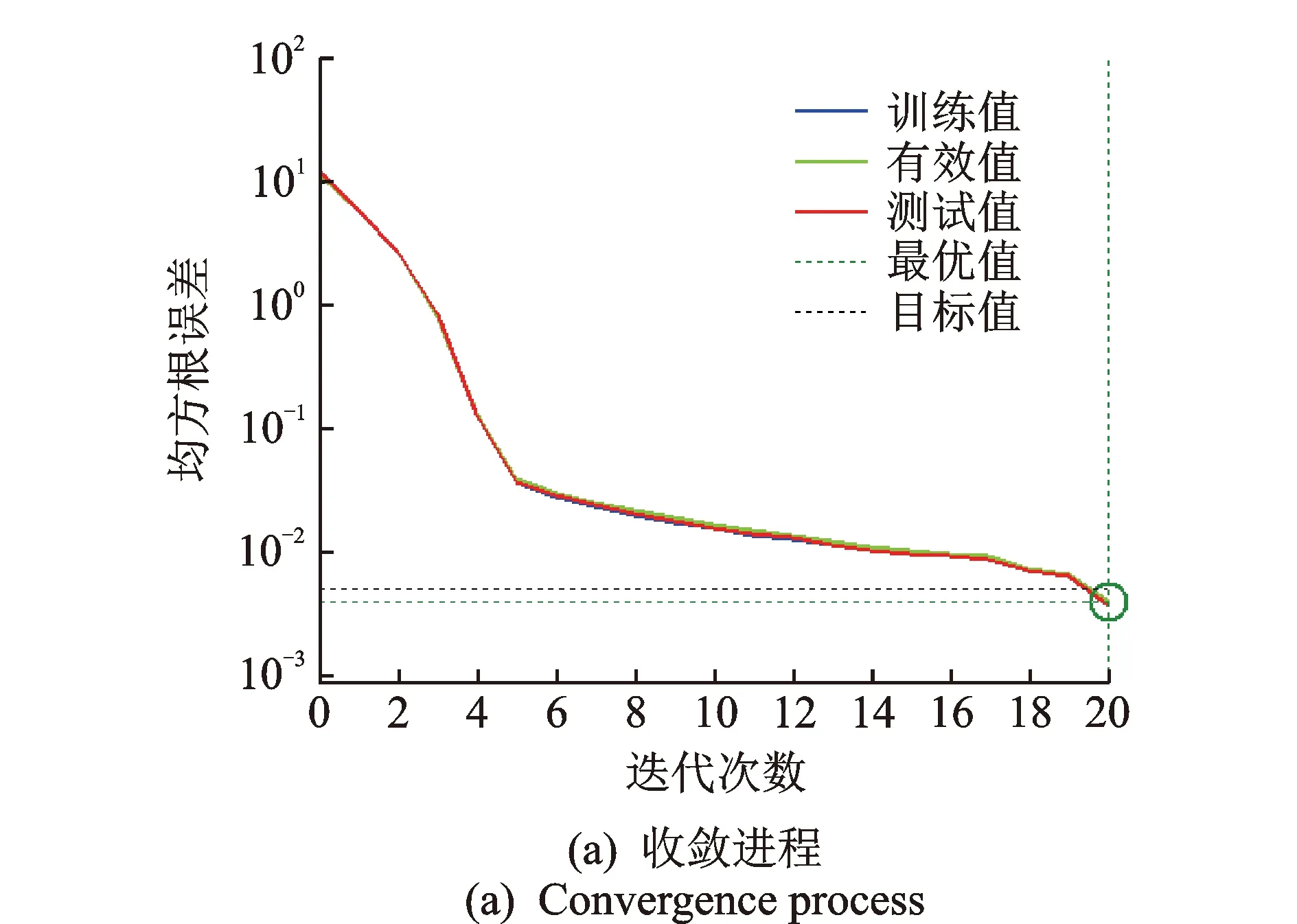
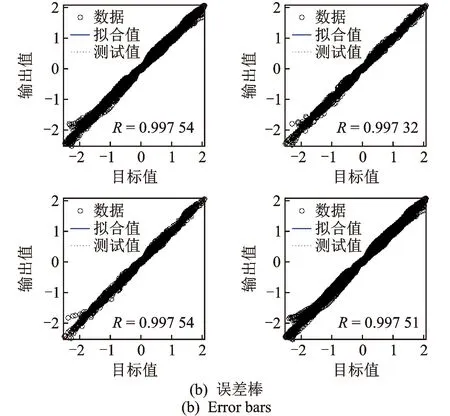
图9 第2组检验数据的收敛进程Fig.9 Convergence process of the second group test data

图10 未优化预测曲线与试验曲线对比Fig.10 The comparison between no optimization forecasting curve and test curve

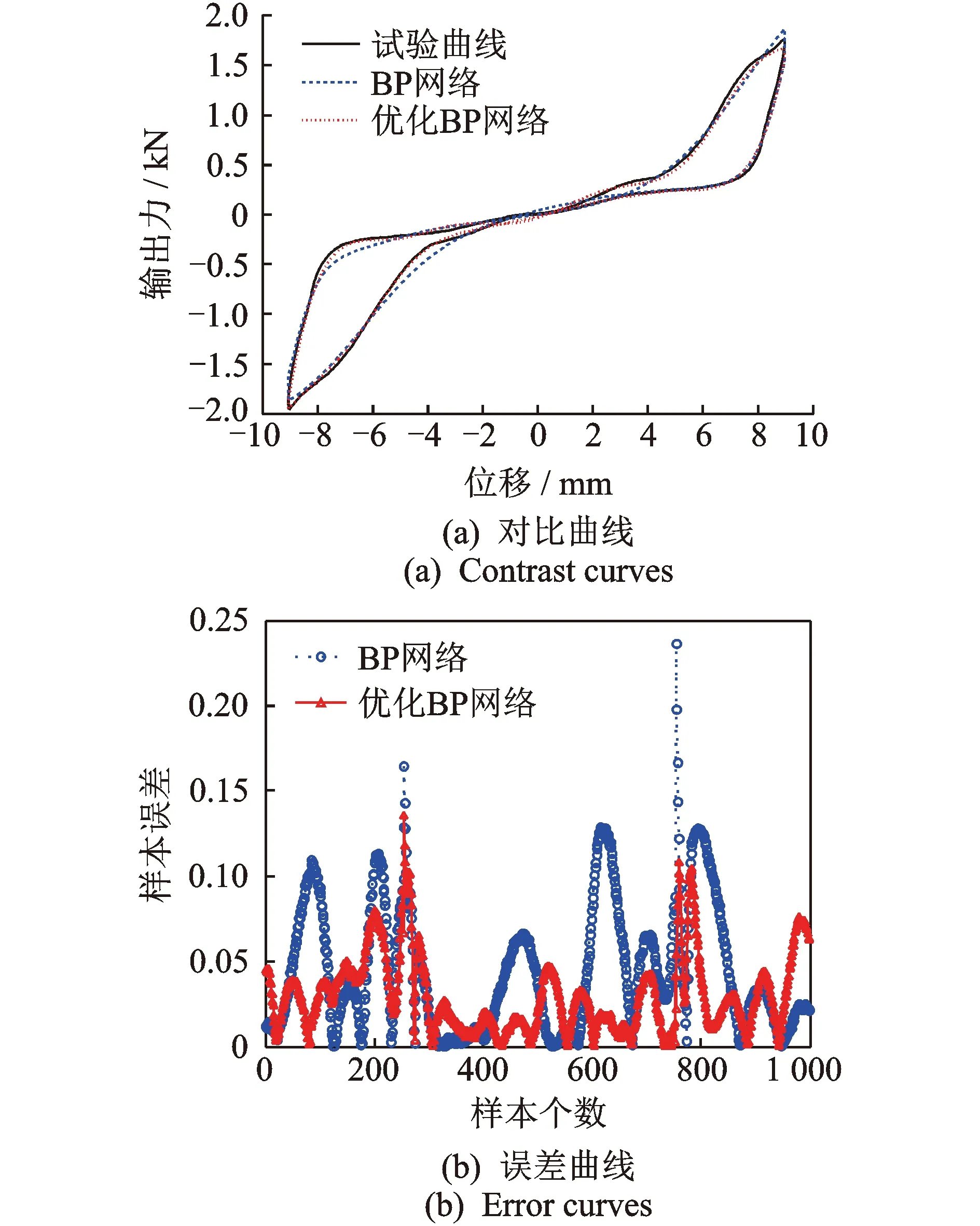
图11 位移幅值9 mm时的预测曲线与样本绝对误差Fig.11 Prediction curve and absolute error at 9 mm

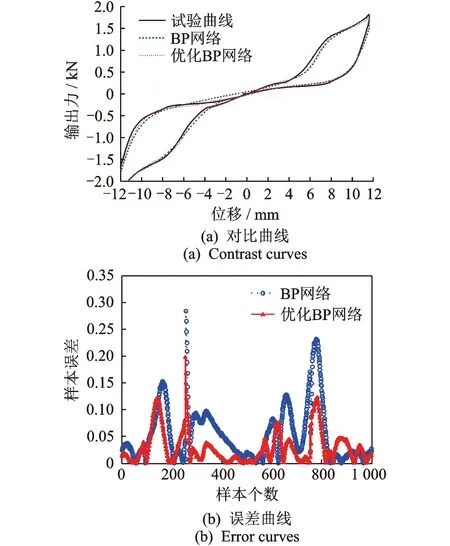
图12 位移幅值12 mm时的预测曲线与样本绝对误差Fig.12 Prediction curve and absolute error at 12 mm

图9为第2组检验数组神经网络预测模型的收敛进程。由于神经网络每次运行得到的结果都在变化，而理论上未优化的BP网络在多次运行中也能找到最优值，因此这里采取随机运行进行优化与未优化对比。图10为随机二次运行的未优化BP预测曲线与试验曲线的对比图。可以看出，由于初始权/阈值的随机性，使每次训练学习后得到的BP网络波动较大。图11，12为试验曲线与未优化BP网络、优化BP网络预测曲线的对比图与样本绝对误差图。可以看出，除个别点偏差较大外，大部分数据点误差控制在0.2 kN以内，能够满足实际应用需要。优化与未优化BP网络模型均能较好地预测复合减震装置在施加电压下的输出力，但优化后BP网络更稳定、精度更高，可以快速得到误差更小的网络模型。

3 结 论

1) 该复合减震装置滞回曲线饱满且基本对称，耗能能力较好，性能稳定。随着电压的增大，滞回环的面积逐渐增大，耗能能力不断增强。在位移幅值为12 mm、电压为120 V下，单圈耗能量提高了138.23%，等效阻尼比提高了94.23%。可见，SMA压电复合减震装置具有较好的半主动耗能能力。

2) 由于神经网络的初始权/阈值为人工免疫算法寻优得到的最优初始权/阈值，相比未优化的BP网络而言，优化后的BP网络提高了预测模型的稳定性，可以更加快速地得到误差更小的网络模型。

3) 除个别点偏差较大外，BP网络模型预测后的大部分数据点误差控制在0.2 kN以内，可以满足实际应用需要，且这种以速率符号、电压和位移为神经元输入的BP神经网络本构模型便于在Matlab中实现，为SMA复合类减震装置本构模型的建立和应用提供了新途径。