2019年北京大学自主招生数学试题(部分)及其详解

甘志国

(北京市丰台二中 100071)

2019年北京大学自主招生数学试题全部是单项选择题.本文中的试题均是由参加考试的学生回忆得出的，因而回忆出的题目可能不准确(没有回忆出选项的题目均改成了填空题)，题目也不全，题号也不准确.解得由笔者给出.

2.若复数z1,z2分别满足|z1-3i|=2,|z2-8|=1，则在复平面上所有由复数z1-z2对应的点围成的面积是( ).

A.4π B.8π C.10π D.前三个答案都不对

3.若从1,2,3,4,5,6,7,8,9中随机地取出四个两两互异的数，分别记为a,b,c,d，则a+b与c+d奇偶性相同的概率是.

4.在正方形ABCD中，K为△BCD内一点，且∠KDB=∠KBC=10°，则∠KAD=( ).

A.45° B.60° C.70° D.前三个答案都不对

5.已知x,y∈Z，若(x2+x+1)2+(y2+y+1)2为完全平方数，则数对(x,y)的对数( ).

A.0 B.1 C.无穷多 D.前三个答案都不对

A.3 B.7 C.1 D.前三个答案都不对

8.若数列{an}满足ak+ak+1=4k+3(k∈N*)，则a2019+a2=，a2020-a2=.

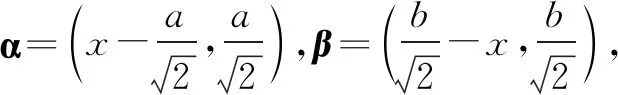
进而可得题设即〈α,β〉=0.

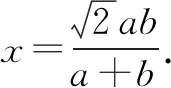
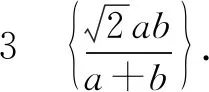
如图1所示，作Rt∠AOB的平分线OX，且OA=a,OB=b,OX=x.

由余弦定理及题设，可得

而由由线段公理，可得AX+BX≥AB，所以AX+BX=AB，即点X在线段AB上.

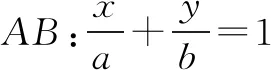
2.B.可得复数z1对应的点Z1(x1,y1)的轨迹是圆x2+(y-3)2=22，复数z2对应的点Z2(x2,y2)的轨迹是圆(x-8)2+y2=12，因而可设

再设复数z1-z2对应的点是Z(x,y)，可得

(x+8)2+(y-3)2=5-4cos(α-β).

因为5-4cos(α-β)的取值范围是[12,32]，所以复数z1-z2对应的点围成的图形是以点(-8,3)为圆心、半径分别为1,3的两个圆组成的圆环，因而其面积是π(32-12)=8π.

(1)a+b与c+d都是奇数，有(2·5·4)·(2·4·3)=960种情形.

(2)a+b与c+d都是偶数，包括下面的四小类(共624种情形)：

图3

在△ADK中，可得AD=1,DK=2sin35°,∠ADK=∠ADB+∠BDK=45°+10°=55°，由余弦定理可得AK2=12+(2sin35°)2-2·1·2sin35°·cos55°=12,AK=1.

因而在△ADK中，可得AK=AD=1，所以∠AKD=∠ADK=55°,∠KAD=180°-55°·2=70°.

5.A.当x,y∈Z时，可设x2+x+1=x(x+1)+1=2m+1(m∈Z)，同理可设y2+y+1=2n+1(n∈Z)，所以(x2+x+1)2+(y2+y+1)2=(2m+1)2+(2n+1)2=4(m2+n2+m+n)+2.

因而(x2+x+1)2+(y2+y+1)2被4除余2，所以(x2+x+1)2+(y2+y+1)2不为完全平方数.

图4

由椭圆的定义，可得|PF1|+|PF2|=2a,

|PF1|2+|PF2|2+2|PF1|·|PF2|=4a2. ①

在△PF1F2中，由余弦定理可得

|PF1|2+|PF2|2-2|PF1|·|PF2|cos2θ

=|F1F2|2=4c2. ②

①-②，可得2|PF1|·|PF2|(1+cos2θ)=4b2,

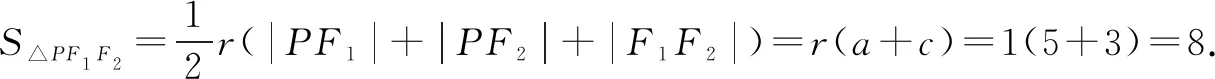
若点P是椭圆Γ的上顶点，可得点P的坐标是(0,4)，进而可得△PF1F2的内切圆半径r满足

=r(a+c)=r(5+3)=8r.

再由椭圆的焦半径公式，可得

8.4043,4036.由题设，可得