一道三角形最值问题的解法探究
2019-08-26 08:05:04曹越程
数理化解题研究 2019年22期
曹越程
(河北省唐山市海港高级中学 063611)
一、例题
下面是石家庄二中高考模拟题的改编题.

题目已知:△ABC为等腰三角形,AB=AC,BD为AC边上的中线,且BD=2,
求△ABC面积的最大值.
分析该题目条件干净利落,内容丰富深刻,解题切入灵活,希望大家有所收获.
二、多种解法
1.构造函数法
通过引进变量,可以选取长度也可以是角度,构造目标函数求得最值.


(2)从腰长切入.设AD=t,则AB=2t,BD=2,△ABD中由余弦定理得:





(4)从顶角切入.设∠BAC=2θ,AB=AC=x,由余弦定理得:


2.平面几何法
通过利用三角形重心的性质,借助正弦定理面积公式求解.
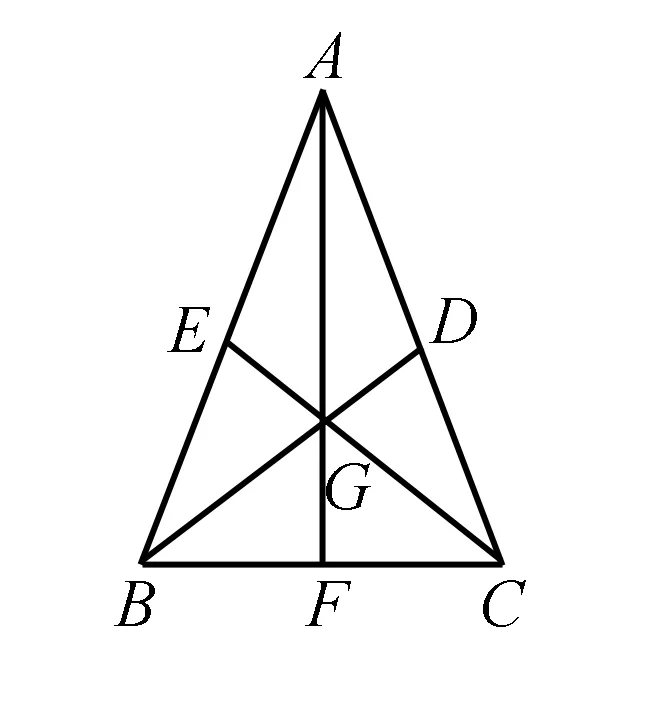


3.解析几何法
建立平面直角坐标系,通过坐标的代数运算求解.






4.极坐标法
极坐标是通过长度和角度来确定点的位置,必要时可考虑在极坐标下解题.
如图:以BD所在射线为极轴建立极坐标系,设A(ρ,θ),D(2,0),

猜你喜欢
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
语数外学习·高中版上旬(2020年7期)2020-09-10 07:22:44
语数外学习·高中版下旬(2020年6期)2020-09-10 07:22:44
语数外学习·高中版下旬(2020年5期)2020-09-10 07:22:44
河北理科教学研究(2020年1期)2020-07-24 08:14:28
河北理科教学研究(2020年1期)2020-07-24 08:14:26
中学数学研究(广东)(2018年23期)2018-03-05 07:54:34
智富时代(2017年4期)2017-04-27 02:13:48
高中生·天天向上(2016年8期)2016-11-22 09:22:46

