多约束条件下机动飞行器末段最优制导律研究

严东升，张 曦，李 强，贾平会，李 军

（北京航天长征飞行器研究所，北京，100076）

0 引 言

随着制导武器机动性能和制导精度的大幅提高，仅有单一脱靶量要求的制导律已经不能满足现代战争的需要，寻求复杂环境多约束条件下的末段制导律具有重要的理论意义[1]。基于末段数据链提供的目标位置、速度及视线角等信息，制导律的设计不仅要考虑理论研究，要满足落点精度、倾角约束及过载需求等严苛条件，还要保证工程实用性，以提高制导武器的作战效能。

近年来，末制导研究主要集中在最优控制理论、滑模变结构控制、自适应控制、预测控制方面[2～4]。基于最优控制理论的弹道成型制导律在文献[5]中首次提出，Paul Zarchan则侧重于终端姿态角约束条件下线性制导系统的最优控制研究。Lee[6]在弹道成型制导律的基础上加入对攻击终端时间约束条件，利用最优控制理论实现对低机动目标的协同饱和攻击。胡正东[7]设计了一种带落角约束的再入机动飞行器复合导引律，在最优导引的基础上引入滑模变结构控制，增强导引律的鲁棒性。Manchester[8]设计了带角度约束的循环迭代比例导引律方法，将有限时间的非线性约束问题变为无限时间线性规划问题。Hu[9]结合自适应控制理论，设计了一种带角度约束的三维自适应比例导引律，通过自适应调整系数，满足落角要求实现垂直攻击。上述制导律设计大多未考虑实际应用终端过载的需求，且制导律中包含难以测量的状态信息，不便于工程应用，适用性差。本文针对当前工程应用中面临的问题，基于最优控制理论，在考虑机动性能、落点精度及倾角约束下，得到工程化的最优制导律，通过分析制导阶次研究制导律特性，最后将末端过载控制到零。

1 多约束最优制导方法建模

飞行器末制导问题的线性动力学模型如图1所示。

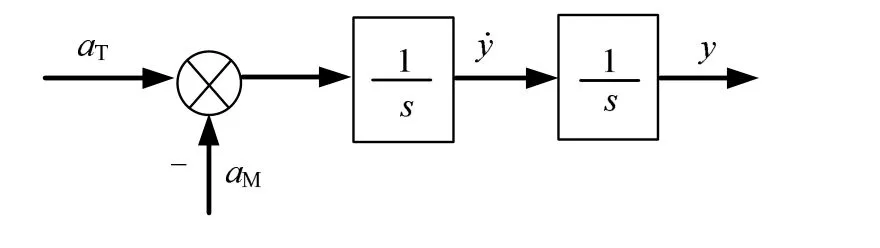
图1 线性动力学模型Fig.1 The Model of Nonlinear DynamicsaT—目标加速度；aM—飞行器加速度；s—飞行器位移

飞行器制导问题的状态方程可表示为

高超声速飞行器通常具有末端位置条件与倾角约束限制，而倾角约束在状态量上等价于末端法向速度约束，可以通过控制飞行器法向速度来满足速度倾角约束，因此末端约束为

制导律设计初期，期望飞行器按较高过载实现大机动飞行，而接近目标时，需要以较小或趋近于零值的过载指令，间接保证飞行器以小攻角击中目标，因此本文引入剩余飞行时间的幂函数R(t)，即：

式中got为剩余飞行时间；n为制导阶次，n ＞0。

定义该制导模型的目标函数为

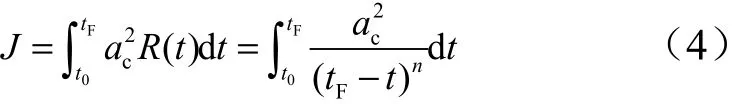
式中 t，0t，Ft分别为飞行器的运动时间、初始时刻及终端时刻。

要使得目标函数最小，即：

根据最优控制理论中对状态空间方程在始、末两时刻的通解算法，该制导问题以飞行器末制导初始时刻为起点，可得末端时刻通解的表达式：

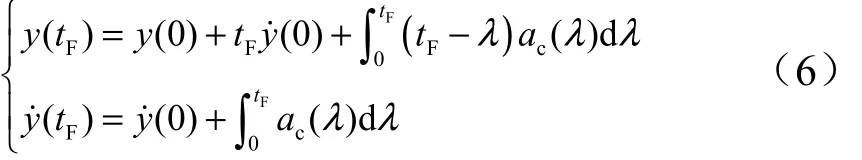
式中 λ为时间变量。

定义函数：

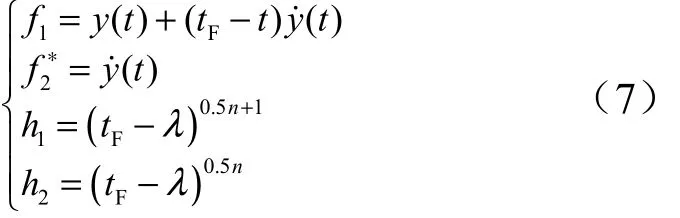
考虑末端位置和法向速度约束，式（7）可简化为

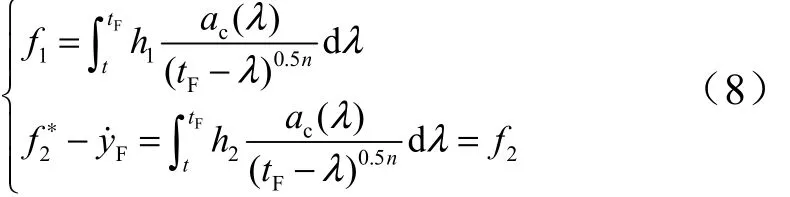
引入中间变量η，将上面两式合并，得到：

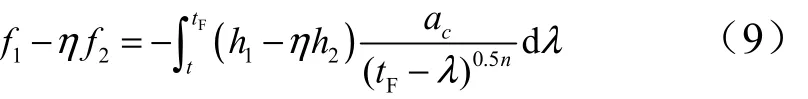
应用Schwartz不等式定理可得：

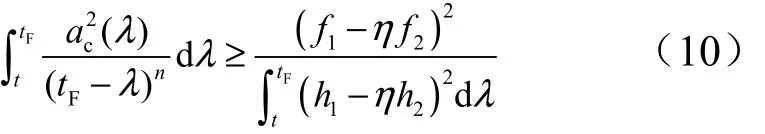
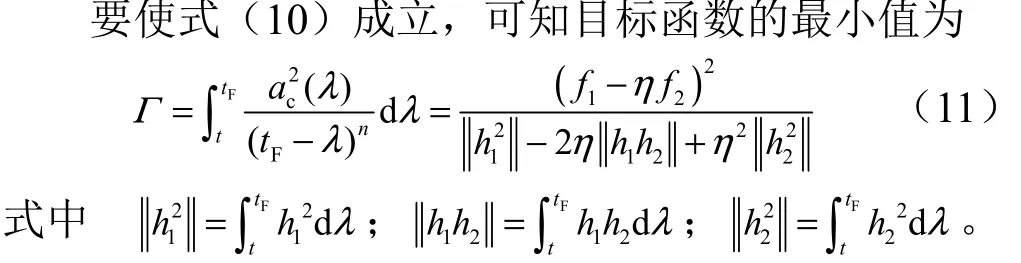
根据Schwartz不等式定理，加速度指令可表示为

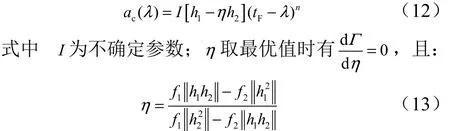
将式（12）代入式（11），得到：

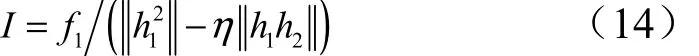
故，飞行器加速度关于t的表达式为

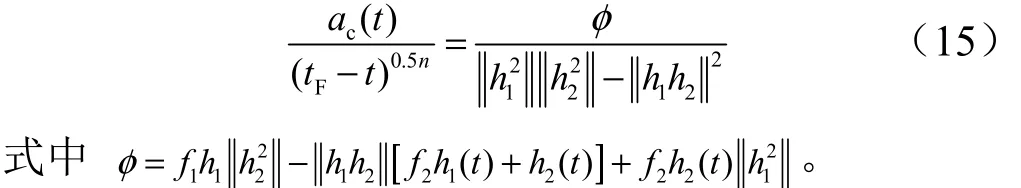
根据1h，2h的定义，在不同时刻存在：

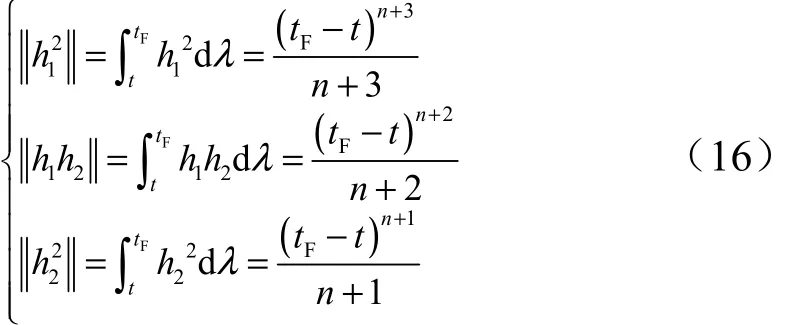
将式（16）代入式（12），可以得到剩余飞行时间tgo的加速度指令为

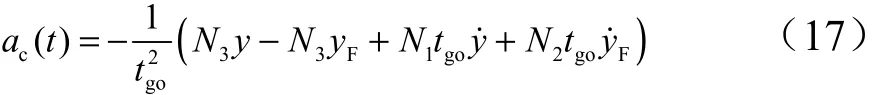
式中 N1及 N3为位置约束权系数，，N2为落脚约束权系数，

2 最优制导律工程简化

式（17）最优末制导律中的状态量，在实际飞行中不便于直接测量，包括飞行器法向位移以及法向速度等，本节对多约束最优末制导律表达式进行简化，以增强工程适应性。末段飞行时间较短，将飞行器和目标看作是在纵向平面运动，建立二维平面交战模型，弹目相对运动关系如图2所示。

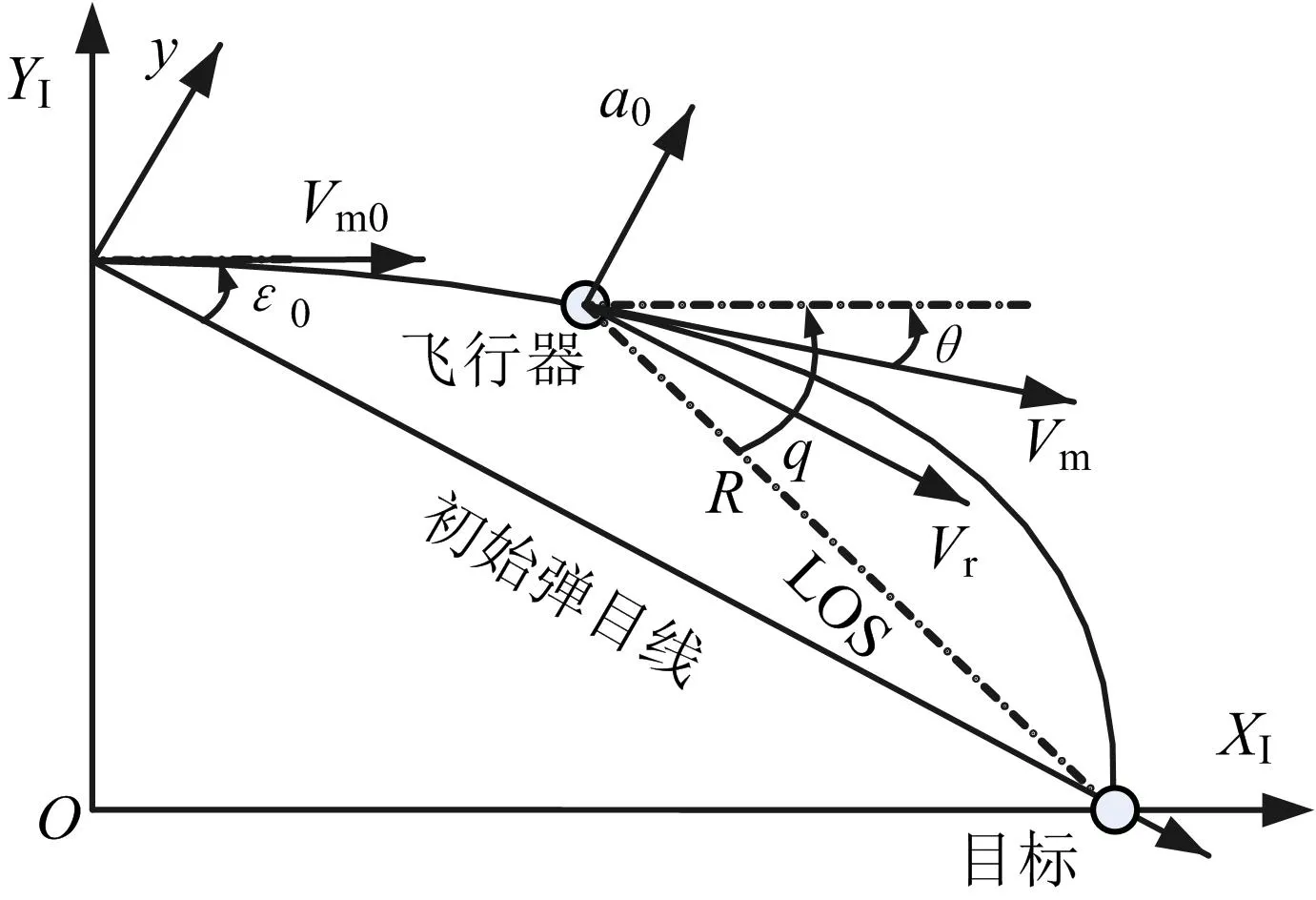
图2 弹目相对运动关系Fig.2 The Relative Motion Relationship between Missile and Target

当q(t)为小量时，根据飞行器与目标几何关系，有：

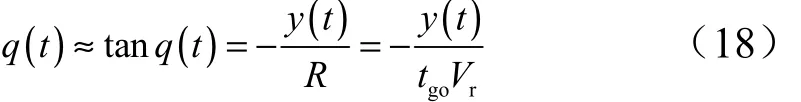
对式（18）两边进行微分，得：

由式（19）可得：

将式（19）代入式（20）得：

将式（20）、式（21）代入式（17）加速度指令中，可得到便于实际应用的多约束最优末制导指令：

式中 q(t)和()q t˙可由导引头测量得到；Fq为提前装订的末端倾角期望值；rV和got可由导航模块进行实时解算。式（22）由末端位置约束项和倾角约束项构成，以实现飞行器的精确打击，并以期望的倾角命中目标。

3 制导律权系数特性分析

3.1 制导权系数对过载影响

由式（17）制导权系数N1和N2与制导阶次n的关系可知，相应的制导指令形式会随着n的变化而变化，因此飞行过载指令也将随之改变。

飞行器的初始位置在弹目视线连线上，基于图 2的飞行器模型，可得法向位移的变化率：

式中0ε为初始速度误差角。

在飞行器末制导初始时刻t=0时，据式（7）可得：

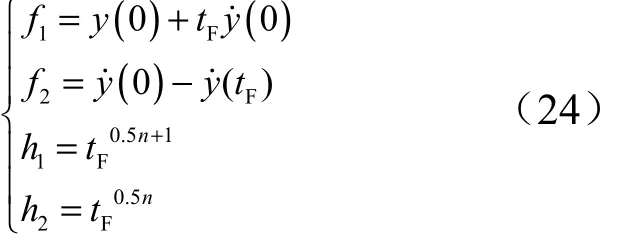
设初始时刻00t= ，由式（16）可得：

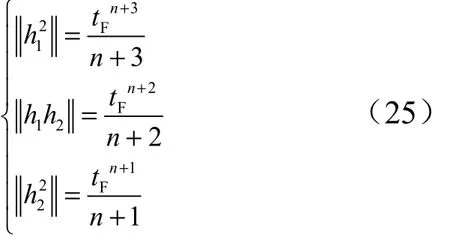
将式（24）代入式（17）中得：

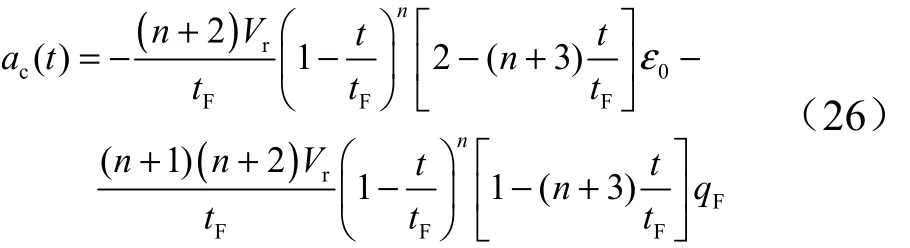
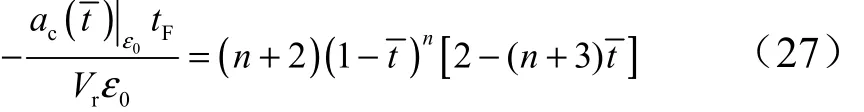
由Fq引起的无量纲过载：

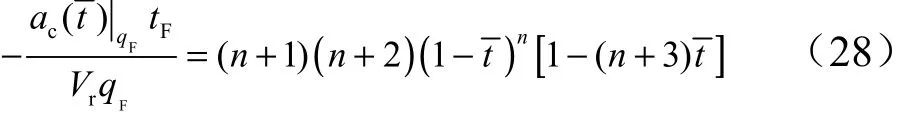
经推导可得，制导律的过载大小主要受制导阶次n的影响，图3给出了不同n值下的由误差角0ε和倾角约束Fq引起的无量纲过载曲线。

由图3仿真曲线可知：

a）当 n=0时，末端位置约束项权系数1N=4，末端倾角项权系数2N=2，制导过程中由0ε引起和由Fq引起的无量纲过载比值保持为2，且两项过载在末端未收敛至零；

b）当n＞0时，由0ε引起和由Fq引起的无量纲过载在飞行末端均收敛至零。由于在飞行前段，已产生足够的制导指令去修正速度方向的误差，飞行后段的速度方向基本调整至弹目视线方向，因此由0ε引起的过载在飞行后段过载指令中所占比重较小。

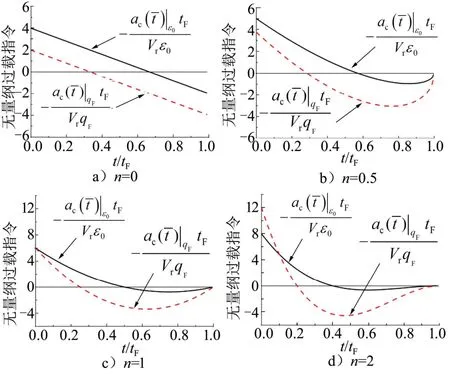
图3 无量纲过载指令曲线Fig.3 Dimensionless Overload Instruction Curve

假设飞行器按1500 m/s的速度飞行，飞行器初始航向角θ0=0°，飞行器初始位置(x, y )= ( 0,30) km，目标静止。取不同的制导阶次，对弹道形式进行计算仿真，得到的弹道形式如图4所示。

当 n越大，由Fq引起的过载指令占比越大，在飞行前段会使用更多的过载指令来满足倾角约束条件；在飞行后段由Fq引起的过载指令也会逐渐减小，过载指令缓慢变化减到零值。

3.2 制导权系数对弹道影响

图4 不同末端倾角约束下的飞行弹道随制导阶次变化曲线Fig.4 Trajectory with Multiple Guidance Order under Different Impact Angle Constrains

由图4可得到：

a）在相同的Fq条件下，随着制导阶次n增加，倾角约束权系数2N变大，倾角约束项过载指令更大，使初始段产生较大加速度，将弹道拉高，因此在初始时刻弹道形态会剧烈地变化；

b）在末制导初始阶段，可以通过降低制导阶次n控制弹道爬升，以减小倾角约束项权系数对弹道形态的影响。

4 末段制导策略设计

利用第1节推导的最优制导律，进行末制导策略设计。该飞行段需要进行较大范围机动飞行，攻角和速度变化较大，为了保证最终命中精度，同时满足末端角度约束条件，纵向选用多约束最优制导律，并加入重力补偿项，惯性坐标系下指令形式为

当制导阶次n增加时，2N所占比重增大，飞行器以较大过载来修正飞行器相对于期望值Fq的速度角偏差，从而降低接近目标时的需用过载；然而制导阶次过大会使得制导权系数过大，间接降低了制导系统抑制信息噪声的能力，导致命中精度降低。基于上述分析，为了满足倾角约束和命中精度的要求，经过试验论证，取n=2，权系数1N=4，2N=2。

侧向采用纯比例导引制导律，惯性坐标系下指令表达式为

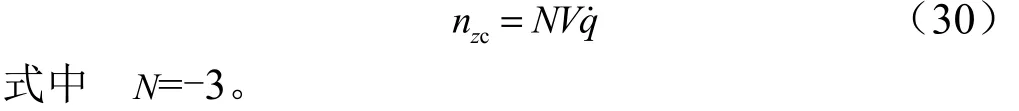
对基于多约束条件下的最优制导策略进行末段的数学仿真校验，给出关于攻角、侧滑角、滚转角及速度倾角的仿真曲线如图5所示，飞行器采用BTT-180控制方式，弹身滚转使其最大升力面转至机动平面，以实现末段的快速下压。

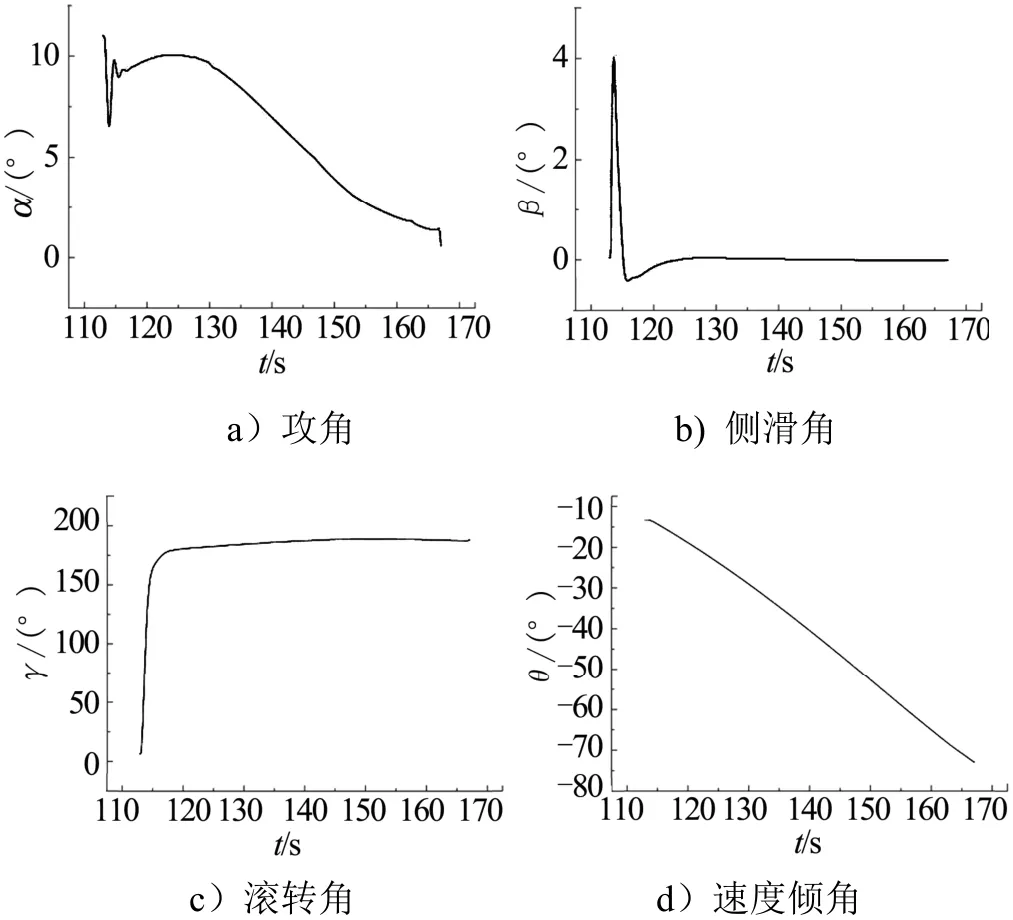
图5 末段攻角、侧滑角、滚转角及速度倾角变化曲线Fig.5 Angle of Attack, Angle of Side Slip, Roll Angle and Velocity Path Angle Curve

由图5可知，末段下压段，由于采用BTT-180控制方式，所以下压段滚转角超过180°，飞行器正攻角飞行，且最终收敛至零附近。对于侧向通道而言，为实现协调转弯，降低导弹飞行过程中的气动力耦合，全程侧滑角小于3°，以增强导弹的协调转弯能力。下压段速度倾角逐渐减小，末端倾角值为-76.53°，满足倾角约束条件。

图6给出了弹体系下纵向和侧向加速度指令跟踪情况，飞行器过载输出以及对指令跟踪效果较好，有利于飞行器BTT协调转弯飞行保证其命中精度要求。在最优制导策略下，减小了需用过载，实现了末端过载接近于零的设计需求，保证以小攻角击中目标。

图6 纵向及侧向加速度指令跟踪曲线Fig.6 Vertical and Lateral Acceleration Command Tracking Curve

图7 给出了飞行器在末制导段运动的三维轨迹图。

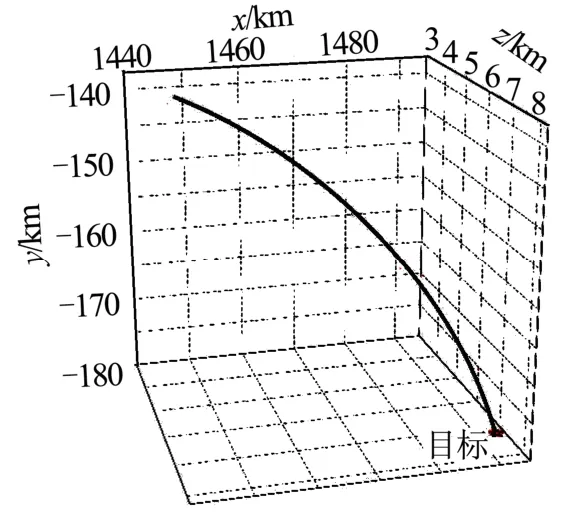
图7 飞行器末段三维弹道Fig.7 Terminal Three Dimensional Trajectory

仿真结果表示该制导律成功导引至目标位置处，末段基本上基于纵向平面内运动，计算脱靶量为2.21 m，满足命中精度的要求。

5 结 论

为实现多约束条件下飞行器末段侵彻攻击任务，本文将最优控制理论与工程应用紧密结合，通过将剩余飞行时间幂函数引入性能指标设计制导律，通过制导律特性分析及数值仿真，验证了该方法的有效性，满足了过载需求、倾角约束和命中精度要求，提高了工程适用性。多约束条件下的最优制导策略设计是实现制导武器末段突防的前提和保证，对实现地面高价值目标的打击与摧毁具有重要工程应用价值。