基于模糊多态贝叶斯网络的地铁运营风险评估方法*

曾明华 王 旭 王转敏 王 敏

(1.华东交通大学交通运输与物流学院，330013，南昌；2.中国铁路兰州局集团有限公司兰州车务段,730050,兰州; 3.兰州市轨道交通有限公司，730030，兰州;4.合肥城市轨道交通有限公司,230001,合肥//第一作者，副教授)

地铁运行环境特殊,系统设备复杂，如果发生事故，将会造成巨大的影响。通过科学有效的方法分析地铁运营安全状况，预防及控制运营安全事故，对保障地铁运营安全具有重要意义。

许多学者从不同的方面对我国地铁运营安全风险评估做了研究。如文献[1]对我国地铁运营安全评价现状做了系统性的分析，并对今后的发展趋势做了展望。然而，这些研究主要针对特定的安全事故或局部安全隐患，如火灾事故[2]、人为因素隐患[3]等，对地铁系统运营安全的研究较少。绝大多数对地铁系统运营安全的研究是将多种方法结合使用，如层次分析法与集对分析原理结合的地铁运营安全评价[4]，层次分析法与熵值法组合赋权的地铁安全评价[5]，网络层次分析法与逼近理想排序法结合的地铁运营安全研究[6]等。这些组合方法使评价结果更加客观，但是适用性一般。多级可拓评估模型[7]以各指标为出发点，确定各指标风险等级。该方法适用性较好，但是处理模糊性问题还有待提高。其他应用较少的方法有解释结构模型(ISM)[8]、数理统计方法等。ISM能较好地处理因素间的关联性，但定量分析较少。数理统计方法[9]能够定量地分析和表达系统的安全性，但需建立完善的历史数据库，否则将会影响结果的正确性。

考虑到地铁运营安全子系统众多，仅对局部风险因素进行分析，不能完全反映地铁运营安全状况，而大多数地铁运营安全的评价研究，又很少同时考虑影响因素间的关联性与因素的多态不确定性。为此，引入能较好地处理因素之间关联关系的ISM和善于表达多态不确定性事件的贝叶斯网络，并综合利用ISM和贝叶斯网络的特征，构建基于ISM和模糊多态贝叶斯网络的地铁运营安全风险评估方法。首先使用ISM分析影响因素间的关联关系，建立结构模型并转换为模糊多态贝叶斯网络结构。然后利用模糊多态贝叶斯网络进行学习与推理计算，实现地铁运营安全风险预测。该方法既考虑了影响因素间的关联性和因素的多态不确定性，又实现了定性分析和定量分析，使计算分析结果更加科学客观。

1 地铁运营安全影响因素分析

影响地铁系统运营安全的因素众多，其中可能导致运营安全事故的因素是最关键的。为选取更加具有科学性、系统性、可操作性和独立性的影响因素，对国内外地铁运营安全事故进行统计分析，并参考《地铁运营安全评价标准》和相关文献[10]，将武汉地铁运营安全影响因素T分为安全管理因素T1、运营组织及人员因素T2、设备设施因素T3和环境因素T4等4大类，并细分为18个影响因素，具体如下：

1)T1是对一切安全生产活动的管理与控制，是保障地铁运营安全最基本、最主要的因素，主要包括安全管理机构S1、应急救援体系S2、安全培训教育S3、生产投入与管理目标S4等因素。

2)T2是保障地铁运营安全的关键因素，主要包括客运组织及人员S5、行车组织及人员S6、设备维护及操作人员S7、外部人员S8等因素。

3)T3为地铁运营安全提供最基本的硬件要求，是保证地铁运营安全的必要条件。依据武汉地铁设备维护部门设置，将T3划分为车辆系统S9、供电系统S10、线路及轨道系统S11、通信信号系统S12、自动售检票系统S13、土建系统S14、电梯及屏蔽门S15、机电自动化S16等因素。

4)T4主要包括内部环境因素S17和外部环境因素S18。S17会影响设备的正常使用、人员的心理变化以及员工对企业的认同感等。S18可能会对地铁运营安全造成重大灾害，常见的有恐怖袭击、地震、暴雨等。

2 原理与算法

主要介绍ISM、贝叶斯网络和模糊集理论，并重点讲述如何将上述方法相结合，构建基于ISM的模糊多态贝叶斯网络风险评估方法。

2.1 原理介绍

ISM是美国Warfield教授在1973年开发的一种系统分析方法。ISM把结构复杂、关系模糊的系统分解为若干子系统，应用实践经验和领域知识，以及计算机的计算，最终构造出1个多级递阶关系的结构模型。它特别适用于要素众多、关系复杂而结构模糊的系统分析[11]。

贝叶斯网络又称信度网络，是美国Pearl[12]教授于1986年提出的。它是一种概率图模型，是在Bayes公式的基础上扩展出的一种不确定性知识表达和推理模型。贝叶斯网络是由网络节点V、表示节点间因果关系的有向边E，以及表示节点间依赖关系的条件概率分布P组成的有向非循环网络，表示为B=〈G,P〉。其中，G=〈V,E〉为有向无环图。

贝叶斯网络具有以下优点：①是图论与概率论结合发展形成的图形化网络，所有网络节点均可见；②在部分数据缺失的情况下也可进行网络学习和推理计算；③具有很强的学习能力，可根据新输入的数据更新网络参数；④可以双向推理计算。

(1)

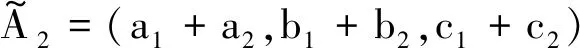
(2)

为方便领域专家给出客观的评判结果，引入自然语言变量：非常高、高、偏高、中等、偏低、低和非常低[14]。将专家给出的评判结果转化为三角模糊概率。每个自然语言变量与三角模糊数的对应关系如表1所示。

2.2 分析步骤

首先，使用ISM分析影响因素之间的相互关系，构建结构模型，进而转换为多态贝叶斯网络结构。其次，进行专家评判，将专家给出的自然语言变量转化为三角模糊数并进行计算，获得先验概率和条件概率分布。再次，由模糊多态贝叶斯网络计算，获得节点概率值。最后，利用最大隶属度准则确定各影响因素的风险概率等级。基于ISM的模糊多态贝叶斯网络风险评估方法具体分析步骤如下：

表1 自然语言变量与对应的三角模糊数[15]

第1步：确定系统因素S1,S2,…,S18，以及系统目标因素T。

第2步：确定因素关系，建立邻接矩阵X=[xij]18×18，其中

(3)

第3步：邻接矩阵X通过布尔运算求出可达矩阵D=[mij]18×18，其中

(4)

布尔运算式为：

D=(X+I)r+1=(X+I)r≠

(X+I)r-1≠…≠(X+I)

(5)

其中，r=1,2,3,…，I是与X同阶次的单位矩阵。

第4步：将可达矩阵D=[mij]18×18分解为可达集、前因集和最高集。

(1)可达集R(Si)：因素Si可以到达其他因素的集合。即可达矩阵第Si行中所有矩阵元素为1的列对应的要素集合。

R(Si)={Sj∈N|mij=1}

(6)

其中，N为因素集合。

(2)前因集Q(Si)：可以到达因素Si的因素组成的集合。即可达矩阵第Si列中所有矩阵元素为1的行对应的要素集合。

Q(Si)={Sj∈N|mij=1}

(7)

(3)最高集T(Si)：可达集与前因集的交集仍是可达集的集合。

(8)

第5步：级间划分，建立结构模型。级间划分以可达矩阵为准则，利用最高集的定义确定本层级因素，并删除可达矩阵中相应元素的行和列。以此类推，确定不同层级中的因素，用Ln表示。根据级间划分和可达矩阵关系，确定各层级因素间的关系，构建结构模型。

第6步：将结构模型转换为模糊多态贝叶斯网络结构。

(1)确定影响因素状态：假设各影响因素都具有3种风险等级状态，分别为j=0可忽略，j=1可接受，j=2不可接受。

(2)贝叶斯网络节点转换：把结构模型中对应的影响因素转换为模糊多态贝叶斯网络节点集V。

(3)贝叶斯网络有向边转换：将结构模型中因素间的因果关系转换为模糊多态贝叶斯网络有向边E。

完成所有转换后，得到模糊多态贝叶斯网络结构。

(1)自然语言变量转化为三角模糊概率。为获得节点概率信息，邀请多位专家分别对各节点不同风险等级状态给出评判意见，第k位专家对节点Si处于风险等级状态j的评判意见通过三角模糊数转化，得到三角模糊概率为Pij,k=(aij,k,bij,k,cij,k)。

(2)三角模糊概率均值化。为得到相对合理的模糊概率值，将各位专家给出的评判结果进行算术平均，得到模糊均值概率。表示为：

(9)

(3)解模糊。采用面积均值法将模糊均值概率转化为最能代表该模糊集合的概率值。表示为：

(10)

(4)归一化。将各节点在不同风险等级状态下的概率值归一化，使概率值满足和为1，得到所需的先验概率和条件概率分布。表示为：

(11)

第8步：模糊多态贝叶斯网络的学习和推理。根据求得的先验概率和条件概率分布，利用模糊多态贝叶斯网络进行学习和推理计算：①通过贝叶斯网络学习计算，获得各节点不同风险等级状态下的概率值；②正向因果推理，根据已知根节点不同风险等级状态下的概率值，推导目标节点的概率信息；③反向诊断推理，根据已知目标节点不同风险等级状态下的概率值，推导其他节点的概率信息。

第9步：风险评估。依据最大隶属度准则[16]，在不同风险等级状态概率分布中，选取概率值最大对应的等级作为各因素风险概率等级。结合模糊多态贝叶斯网络反向诊断推理能力，进一步找出目标因素T发生事故时关键的影响因素。

3 案例分析

采用建立的风险评估方法对武汉地铁运营安全进行分析。利用MATLAB软件和Netica软件进行计算，验证该风险评估方法的正确性和科学性。

第1步：确定影响因素，见第1节所确定的影响因素。

他们迅速研究对策，也不乏一些巧妙的方法，却无一经得起现实的考验。眼看灾难即将降临，悲剧似乎无法避免，沮丧的舰长正要命令船员弃舰逃生时，一个叫弗雷泽的士兵喊道：“快拿消防水管来！”这一声叫喊，仿佛醍醐灌顶，让人眼前一亮，消防水管很快被拿来了，士兵用高压水流制造出一条水带，将水雷带到远方，然后用舰炮引爆了它。

第2步：经深入分析与实地调研，根据式(3)建立邻接矩阵X。

第3步：根据式(5)对邻接矩阵X进行布尔运算。经计算，当r=5时，D=(X+I)6=(X+I)5≠(X+I)4≠…≠(X+I)，求出可达矩阵D=(X+I)5。其中:

第4步：由式(6)～(8)对可达矩阵D进行级间分解，确定可达集R(Si)、前因集Q(Si)和最高级T(Si)。

第5步：根据式(8)最高集定义确定1～6级影响因素集合，分别为L1=[S5,S6,S16]，L2=[S8,S9,S12]，L3=[S10,S11,S13,S15]，L4=[S7,S14]，L5=[S2,S3,S17,S18]，L6=[S1,S4]。根据各层级影响因素和可达矩阵关系，建立武汉地铁运营安全结构模型(如图1所示)。该模型是具有7层的多级递阶结构，目标层为武汉地铁运营安全影响因素T。

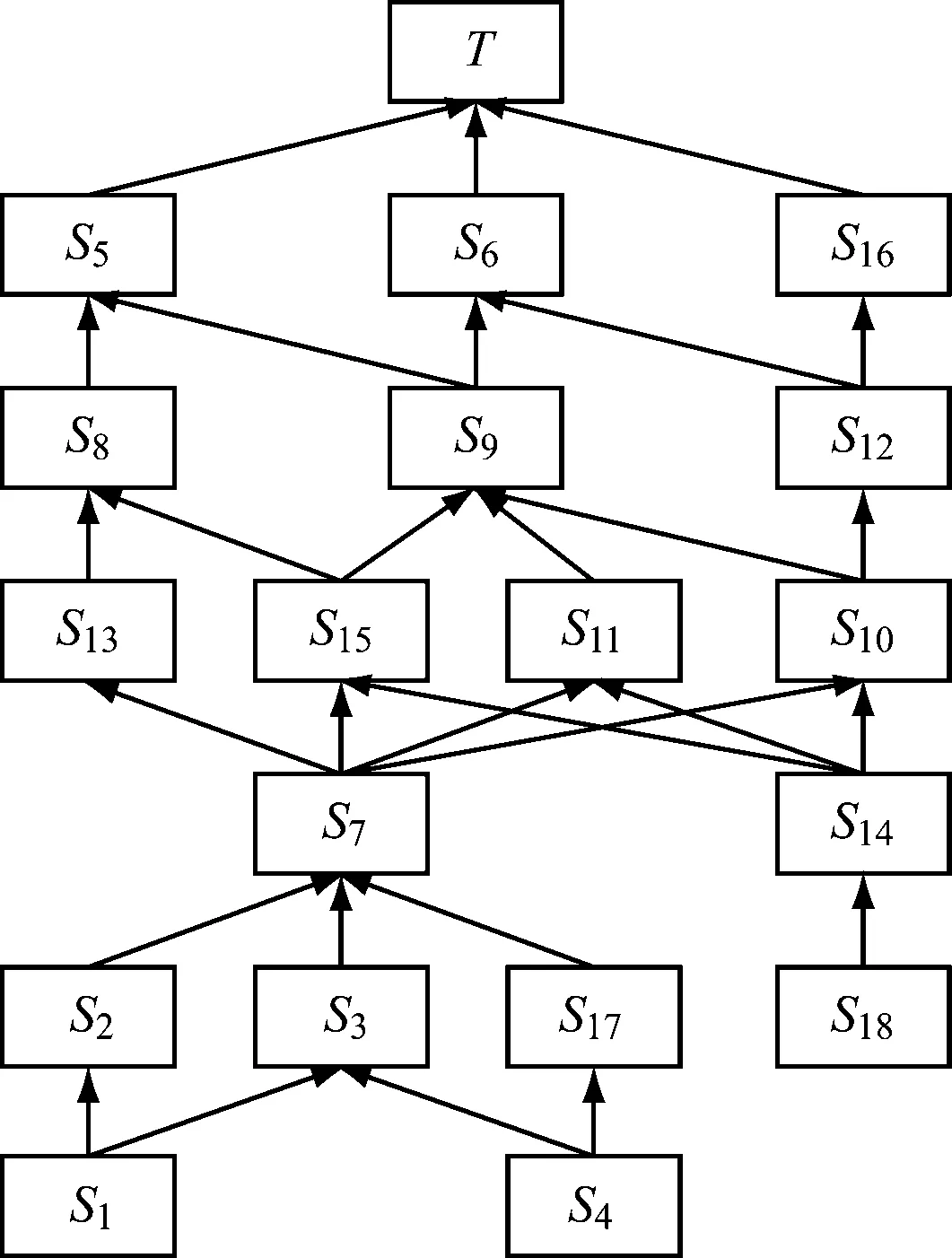
图1 武汉地铁运营安全结构模型

第6步：将武汉地铁运营安全结构模型转换为模糊多态贝叶斯网络结构，具体转换步骤见第2.2节第6步。

第7步：邀请4位专家分别对武汉地铁运营安全的模糊多态贝叶斯网络根节点S1、S4、S18的每种风险等级状态给出评判意见[2]。专家意见如表2所示。

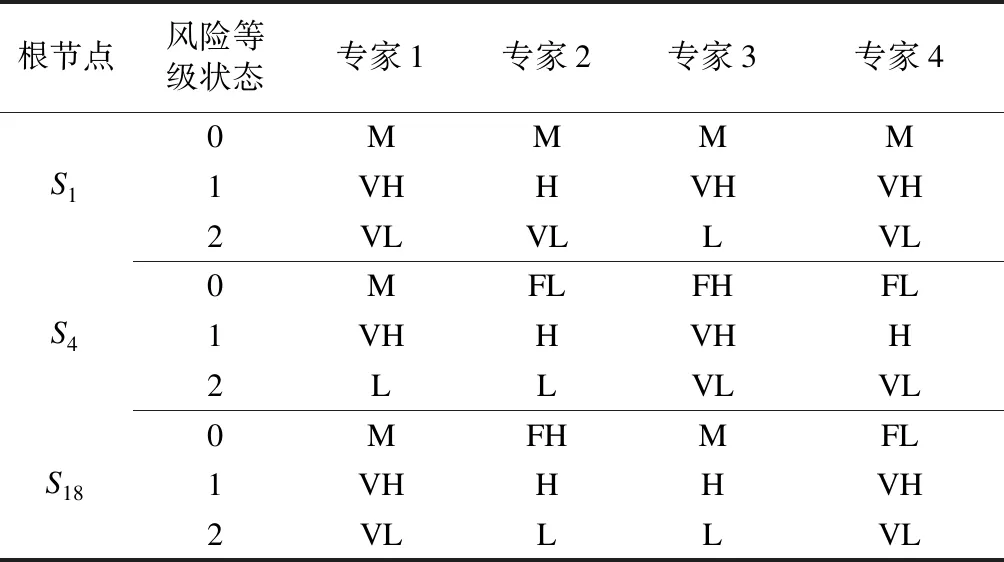
表2 根节点各状态专家评判意见

设各位专家权重值相同，由表2及式(9)～(11)计算出根节点的先验概率P(S1)=(0.310，0.655，0.035),P(S4)=(0.310，0.638，0.052)，P(S18)=(0.333，0.617，0.050)。同理，可计算出其他节点的条件概率分布。

第8步：根据计算获得的先验概率和条件概率分布，利用Netica软件对模糊多态贝叶斯网络进行参数学习，得到各节点在不同风险等级状态下的概率值，以及反向推理计算目标节点T在风险等级状态为不可接受时其他节点的概率信息，如表3所示。

第9步：依据最大隶属度准则确定各因素的风险概率等级。由表3可知，武汉地铁各影响因素的风险概率等级均为可接受。当目标因素T的风险概率等级处于不可接受时，因素S6、S9和S12的概率值发生较大变化，风险概率等级由可接受变为不可接受。

通过ISM得出的武汉地铁运营安全结构模型比较全面客观地反映出武汉地铁运营安全各影响因素之间的关联关系，将结构模型转为模糊多态贝叶斯网络结构，同样保留了影响因素间的关联关系，使贝叶斯网络结构更加客观。

由于篇幅所限，仅对反向推理计算进行分析。当目标节点T的风险概率等级为不可接受时，S6、S9和S12的风险概率等级由可接受变为不可接受，说明因素S6、S9、S12对武汉地铁运营安全具有重要的影响，应加强对这些因素的管理，保障武汉地铁运营安全。同时，因素S18和T1(S1～S4)概率变化不明显，说明目前武汉地铁运营安全管理状况良好。

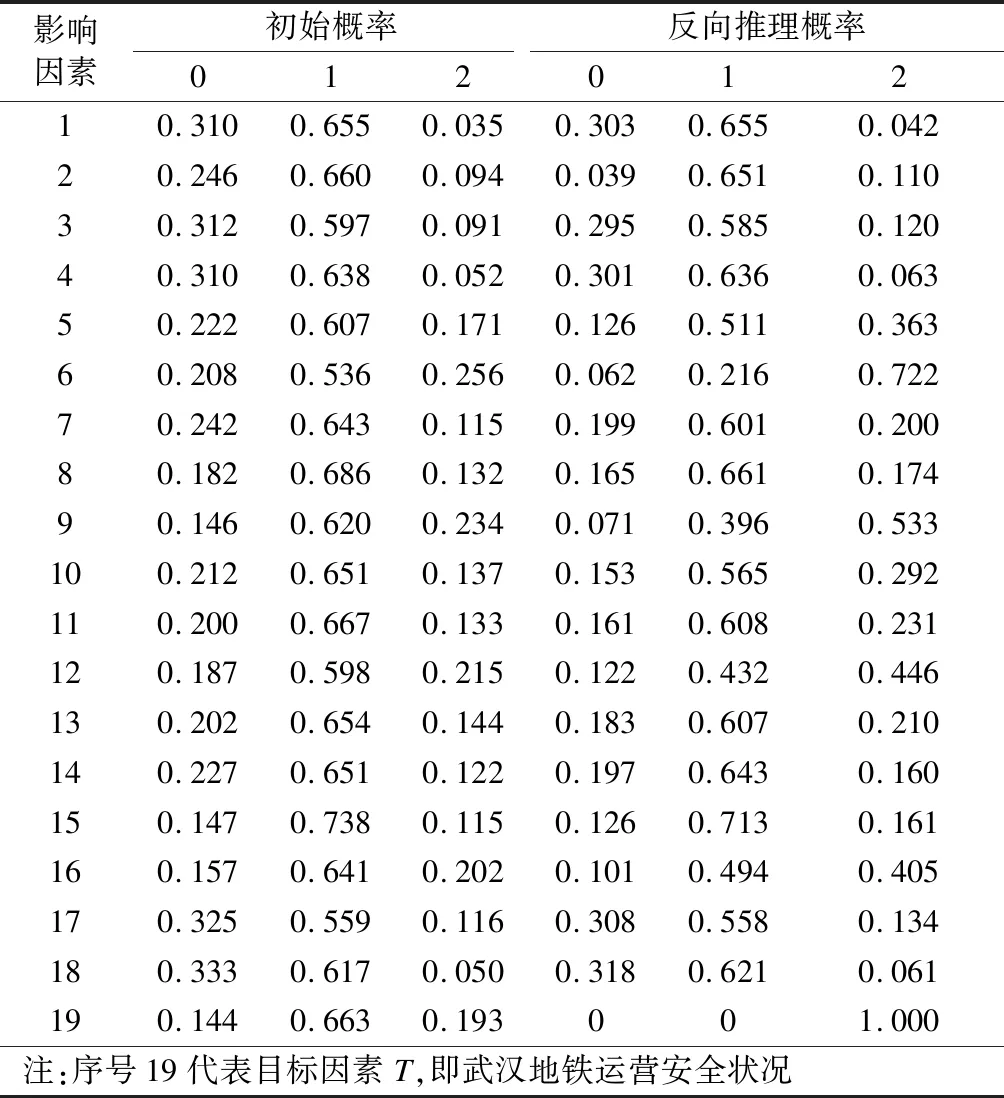
表3 模糊多态贝叶斯网络初始概率及反向推理概率

此外，对武汉地铁2016年度5 min以上运营安全故障进行统计分析，结果如下：全年未发生人员伤亡及重大安全事故；发生5 min以上运营延误事故共28起，运营准点率达99.95%；有效控制了雨水倒灌对地铁运营造成的影响。这说明武汉地铁运营安全管理状态良好，武汉地铁运营安全风险概率等级为可接受。

4 结语

安全是地铁运营企业的生命线，是实现企业经济效益和社会效益的保证。本文综合利用ISM和模糊多态贝叶斯网络对地铁运营安全进行风险评估。该风险评估方法在考虑地铁运营安全各影响因素相互关系的基础上，采用ISM建立模糊多态贝叶斯网络结构，并利用模糊多态贝叶斯网络进行风险概率计算，既降低了构建多态贝叶斯网络结构的复杂度，扩充了网络节点的状态，又充分利用模糊多态贝叶斯网络进行概率推理计算，使计算结果更加科学合理。同时，模糊多态贝叶斯网络能较好地处理多态不确定性问题，从而扩展了贝叶斯网络的使用范围。

通过实例分析得出：武汉地铁运营安全风险概率等级为可接受；当目标因素风险概率等级为不可接受状态时，关键性的影响因素为行车组织及人员因素、车辆系统因素和通信信号系统因素。计算分析结果与实际情况相吻合，验证了该风险评估方法的正确性与实用性。预测和诊断结果可为地铁运营安全管理决策提供支持，有助于提高地铁运营安全，实现安全生产。该风险评估方法可推广至地铁运营安全任意子系统的风险分析及特定安全事故研究。

经典贝叶斯网络模型在节点的概率密度犹豫度较大时会得到相矛盾的结果，而直觉模糊理论在考虑节点确定性与不确定性信息的基础上增加犹豫度，能更细腻地描述节点属性。因此，将进一步结合直觉模糊理论和贝叶斯网络模型，建立更加准确可信的地铁运营安全评估方法，并开发智能监控系统，通过实时收集指标数据，实现对地铁运营安全的实时监控和预警。