二孩政策下的人口系统模型研究
谭景宝 李明
(1. 合肥幼儿师范高等专科学校基础部, 合肥 230013; 2. 安徽文达信息工程学院, 合肥 231201)
近年来,我国政府对计划生育政策逐步作了重大调整。自2015年开始,已全面实施二孩政策。人口问题是一个复杂的系统工程,生育政策的变化,必然会使人口数量、人口质量和人口结构发生变化。在这种新形势下,原有的人口系统模型研究也需随之调整,以适应新的人口发展趋势。本次研究将在现有人口系统模型的基础上[1-4],探讨二孩政策下的人口系统模型,建立和补充新的人口系统模型。
1 常用人口系统模型
1.1 非线性人口发展方程
简单描述生物种群模型:
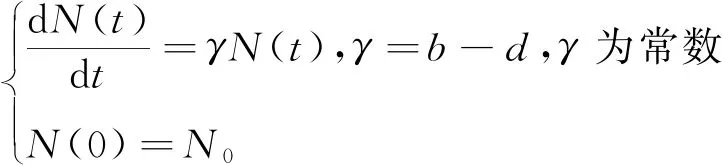
(1)
在方程组(1)中,通过微分公式,对种群群落数量N(t)变化的速率进行分析,即分析离散状态下的时间与种群数量关系。其中,b为种群群落的出生系数;d为种群群落的死亡系数;γ为种群群落数量N(t)的增长系数。
Malthus人口模型:
(2)
方程组(2)与方程组(1)在函数表达形式上有着一定的相似性。p(t)代表的是不同时间的人口增长系数,即相关研究内容方面的种群样本总数。然而,方程组(1)中种群群落的增长系数在种群总量增加的情况下却不断降低,这不利于种群群落人口数量的研究。针对此问题,可应用Logistic分析法构建相关模型,使其与生态学中的人口模型研究相适应。具体模型如方程组(3)所示:
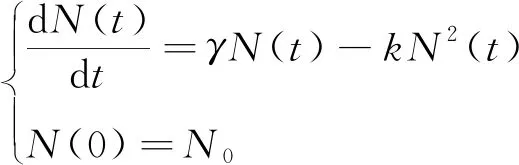
(3)
在方程组(3)中,某一时刻t的种群群落总数为N(t),种群环境生存常数为k,种群生活环境的实际容量(也称种群增长系数) 为γ。相对于方程组(1)(2)来说,方程组(3)的适用性较强。在此基础上,推导出与我国人口发展相适应的模型,如方程组(4)所示:

(4)
在方程组(4)中,p(t)表示在t时刻某一稳定环境中的人口总数情况。其中,δ0为环境总量,ω0则为其人口增长系数。利用假设法,假设稳定生态环境中人口出生、死亡与年龄均无相关性。方程组(4)能够在一定程度上应对传统线性人口动力学模型对人口数量增长与自然资源的适应性问题。由此,得到对应的适应模型:
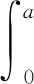
假设增量h>0,用方程表示为:
(5)
dp(a,t)代表的是t p(a,0)=p0(a) (6) 这里忽略了迁移的影响,仿照方程组(4),假设: d(a,t)=[μ(a,t)-kN(t)]p(a,t) (7) 在方程(7)中,μ(a,t)为死亡率相对函数,k是环境容量,N(t)为在t时刻下社会人口总量。设p(a,t)可微,则有: (8) 结合式(6)、(7)、(8),得到式(9): =-[μ(a,t)-kN(t)]×p(a,t) (9) 考虑迁移因素,则有式(10): =-[μ(a,t)-kN(t)]×p(a,t)+f(a,t) (10) 于是,得到非线性人口动力学方程: (11) 其中:p0(a)、β(t)、h(a,t)、k(a,t)分别代表最大育龄总数、规格化条件、生育模式、总和生育率。方程组(11)有别于线性动力学方程,式中社会死亡率和总人数相关,即人口的生存依赖于人口总容量。 我们提出的非线性人口动力学方程,可以更准确地反映社会人口的出生与死亡与其总容量的关系。在方程(6)中,令 d(a,t)=μ(a,t,N(t))p(a,t) (12) 为了区分,称μ(′, ″ ,′)为死亡率,设β(a,t,N(t))为t时刻年龄为a的个体在平均单位时间内的平均生育量,即生育率。β依赖N(t),则边界条件为: (13) 设人口初始密度函数为 p(a,0)=p0(a) (14) 结合式(6)(12)(13)(14),得到方程组(15): (15) 在方程组(15)中,f(a,t)代表t 通常,对于较短时间内的人口状态预测,大多进行简单化的处理即可。在这一时间段内,需要以生态环境的稳定为前提,人口出生、死亡率与时间无相关性,而仅受样本年龄的影响。采用年龄作为人口数量变化的函数参量,所得短期人口数量预测结果较为准确。需要注意的是,社会生态环境的稳定主要包括人口性别比例的稳定,以及生育率、死亡率的保持。在此情况下,可以通过式(16)推导人口发展公式: (16) 在相对封闭稳定的社会环境中,外部迁入人口为零,即迁移率f(a,t)=0。基于模型分析的人口发展非线性方程所涉及的变量只有内部样本的年龄,由此可以得到方程组(15)的变式,即式(17): (17) 参数意义同方程组(15),仍假定社会封闭。这里Q=(0,a+)×(0,T),其中a+,T∈(0,+∞)。 在庞大的人口基数影响下,我国人口发展呈现出明显的“倒金字塔”形状。近年来,人口老龄化现象日益严重,男女比例失衡,人口红利已经明显低于东南亚地区国家。这在加重年轻人经济负担的同时,也削弱了我国经济发展的优势。为解决这一问题,我国政府在坚持贯彻计划生育基本国策的同时,全面放开二孩政策,以应对当前人口结构失衡所带来的问题。面对此问题,可以利用Leslie模型进行人口系统模型研究。首先,选取具适应性的评价指标。在Leslie模型中,所选取的相关模型指标为人口老龄化模型、新生儿出生率、适龄劳动人口数量、不同年龄段人口总数等。然后,构建人口系统模型。 构建人口系统模型,需合理分配人口系统模型的年龄段。为了保证人口系统模型的稳定,内部性别比例需要保持恒定,并能够通过其比例系数进行相应性别人数的推断。在模型构建过程中,可以按年龄段分组。用i表示研究样本的年龄范围,用j表示时间段,划分区间为10 a。 考虑到女性生育年龄的限制,当女性分组超过m之后,模型就没有了实际意义,由此带来的影响也就可以忽略不计。 将女性年龄分为m+1组,通过下式得出不同组别之间人员的转换关系。 将矩阵A代入以上方程组后,可得:Nj+1=ANj。 矩阵A就是Leslie模型的命名依据,该矩阵也就是Leslie矩阵。如果矩阵中的群向量N0=(N(0,0),N(1,0),…,N(m,0))T明确,则该稳定环境下的样本年龄分布情况可以通过迭代的方法进行如下计算: Nj+1=ANj=…=Aj+1N0 为了降低研究难度,可以针对育龄妇女的结婚年龄和二胎生育的时间间隔调整h(i,j),使其指标能够达到最优状态。在此情况下,对Leslie模型变换如下: Nj+1=[A(j)+B(j)]Nj 对于某一时间段内,h(i,j)k(i,j)与j无相关性。根据Leslie系统模型的构建结果,将人口年龄按照0~25、26~45、46~65、66~85、86~105岁进行区分,并绘制人口数量的变化曲线。按照不同年龄段的人口总数,根据Leslie矩阵计算其特征向量。在人口增加的情况下,特征向量的值大于1;在人口减少的情况下,则特征向量小于1。为实现基于全面二孩政策的人口总数增加,则需要增加Leslie系统模型的特征向量值。 按照当前我国人口结构的实际情况,在没有人口出入的情况下,我国人口总数的Leslie模型将呈现出先降低、后增长的趋势。在历时25 a之后,人口规模将达到最大,人口总数保持一定时期的稳定,然后缓慢下降。所以,人口基数的大小及整体人口年龄结构的分布情况,将直接影响到Leslie系统模型的分析结果。 在使用Leslie系统模型的过程中,其中变量关系主要为人口与时间的关系。随着时间的变化,不同年龄段人群的数量也会随之发生改变。借助离散数学分析方法,可以通过矩阵的特征根进行人口发展趋势的预测,其预测结果的准确性较高。基于二孩政策的Leslie人口系统模型中,老龄人口的比重将持续增加,这在一定程度上反映了我国计划生育政策的不足。二孩政策的实施并不能立即解决当前我国所面临的人口老龄化问题。通过人口结构的合理调整,可以使人口老龄化问题逐步得到缓解。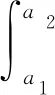
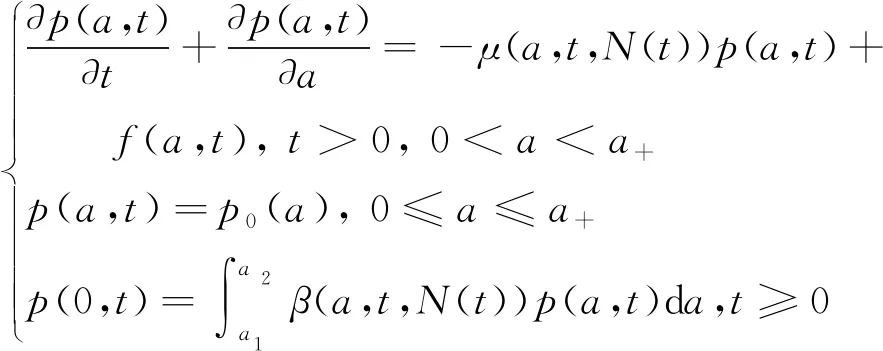
1.2 定常人口预测方程
2 Leslie模型
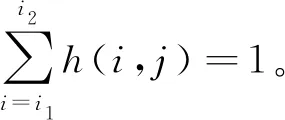
3 结 语

