电磁学中的表格对比学习*
聂传辉 孙立平 刘 祥 阳 启 李伽鹏 高孟毅
(北京建筑大学理学院 北京 102600) (北京建筑大学测绘学院 北京 102600)
在大学物理学习中,电磁学知识由于涉及矢量和微积分运算,对学生而言属于偏难内容.历来在讲授这部分内容时,教师总会感到学生学习吃力.如何寻求更好的教学方法,使学生快速牢固掌握所学内容,是每一个教师要思考的问题.
赵凯华、陈熙谋两位先生在新概念物理教程《电磁学》中,通过列表作了“磁介质两种观点以及与电介质的对比”和“磁路与电路的对比”[1],体现了电、磁的一种对称美,阅读起来也更简捷明了.受这些表格启发,笔者通过长期的教学积累,对电磁学的一些内容进行了表格归纳对比,并用于教学中,取得很不错的教学效果,归纳如下.
1 平板电容器中全部插入介质后对物理量的影响
一般教科书中[2],在讨论平行板电容器中插入介质是否对一些物理量(如电荷量、场强、电压、电容和电场能量等)产生影响时,平板电容器通常具有两种状态:一是电容器充电后与电源断开,一是电容器一直与电源相连.学生在学习这一部分内容时,往往容易把两种情况混为一谈,我们在讲课中列出了表1.让学生把相应内容填在相应位置.提醒学生插入电介质后,两种情况下分别是电荷量Q和电压U12不变,电容C变大.再依据所学知识,把余下的表格填完整.通过这种对比方式,不仅使学生巩固了相关公式,而且介质对物理量产生的影响也一目了然.

表1 平行板电容器中全部插入介质后对物理量的影响
2 散度和旋度的对比
在电磁场与电磁波学习中,散度和旋度的概念学起来都比较抽象[3,4],利用表格对比使学习变得简捷明了,如表2所示.

表2 散度和旋度的对比
3 3种正交曲面坐标系的对比
根据电荷、电流的分布不同,常采用直角坐标系、柱坐标系或球坐标系来处理问题[3,4].表3是关于3种曲面坐标系的对比图,我们让学生在表3图示中标出位置矢量OP,P点在xOy平面上的垂足P′和微分线元PP″,并依次填写出各坐标系的分量、单位矢量、位置矢量、微分线元、面积元和体积元等.实践表明,这种对比方式能很好地帮助学生理解掌握曲面坐标系.

表3 正交曲面坐标系的对比
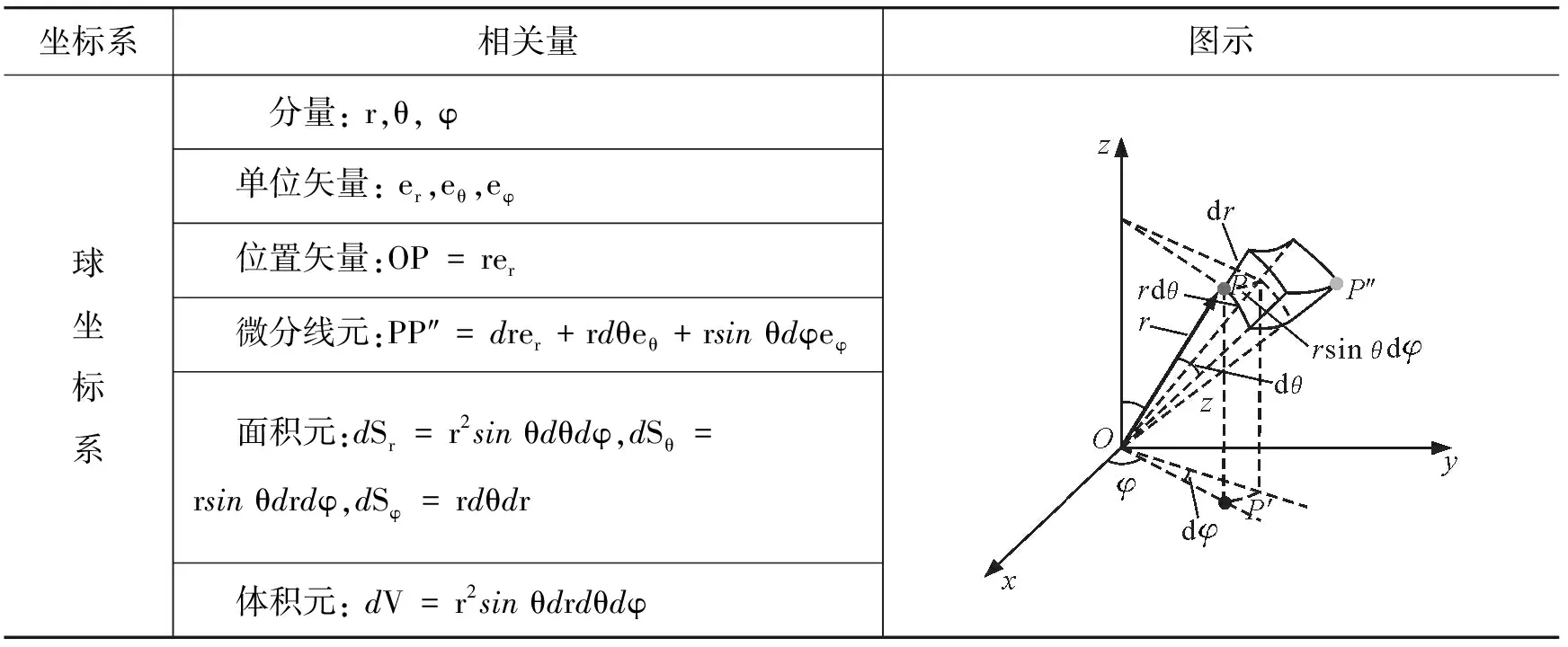
续表3
4 磁介质与电介质的对比
对磁介质与电介质的研究在电磁学领域具有十分重要的意义.在文献[1]中,赵凯华、陈熙谋两位先生通过列表作了“磁介质两种观点以及与电介质的对比”,我们把教程中的表4-2 作了扩充,使知识体系更为完整(见表4).依据静电场E的性质,可引入标量电位φ,并建立均匀电介质中关于φ的泊松方程,通过对比,我们可以很快引出矢量磁位A并建立起关于A的矢量泊松方程,同时写出A的解.
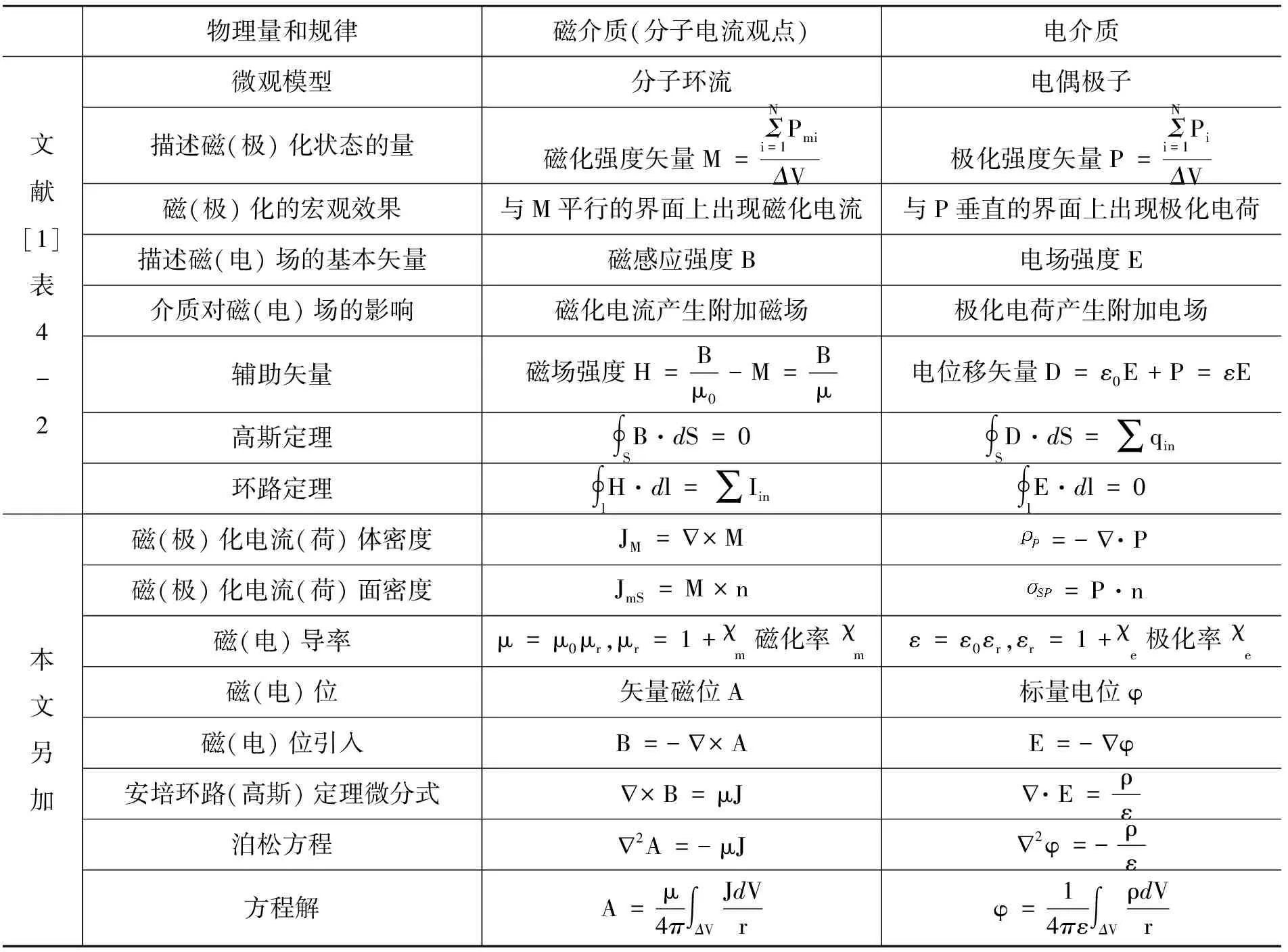
表4 磁介质与电介质的对比
总之,表格对比学习法可调动学生主动学习的积极性,促进学生积极思考,由此及彼,突出知识的连贯性和对称美,是电磁领域学习的一种很好的学习方法.

