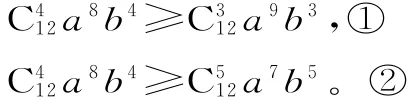二项式定理优卷(B卷)答案与提示
一、选择题
1.B 2.C 3.D 4.B 5.A 6.D 7.D 8.A 9.D 10.A 11.C 12.D 13.D 14.A 15.B 16.B 17.D 18.B 19.B 20.D 21.A 22.C 23.C 24.D 25.B 26.A 27.C 28.C 29.B 30.A 31.A 32.C 33.D 34.A 35.B 36.C 37.D 38.D
二、填空题
39.11 40.-2 41.810 42.28 43.9 4445.70 46.35 47.0 48.8 49.2018 50.-5120 51.五 52.3 53.35 54.-20 55.63 56.3 57.0
三、解答题
58.由题意知。
解得n=6,第4项的二项式系数最大。
故(xlgx)3=20000,即x3lgx=1000,
59.令x=1,得a6+a5+a4+a3+a2+a1+a0=26=64;
令x=-1,得a6-a5+a4-a3+a2-a1+a0=(-4)6=4096。
两式相加,得2(a6+a4+a2+a0)=4160,故a6+a4+a2+a0=2080。
60.(1)(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11。
令x=1,得a0+a1+a2+…+a11=-26。①
又a0=1,所以a1+a2+…+a11=-26-1=-65。
(2)再令x=-1,得a0-a1+a2-a3+…-a11=0。②
①+②得:
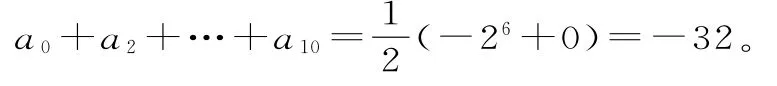
61.(1)设m为正整数,则23m=(23)m=(7+1)m=7k+1,k∈Z。
23m+1=2·23m=2(7k+1)=7(2k)+2;
23m+2=7(4k)+4。
故当且仅当n=3m(m∈N*)时,2n-1能被7整除。
(2)由(1)可知:
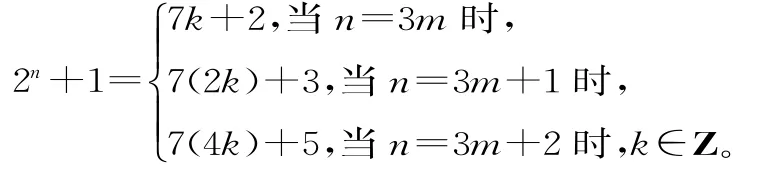
故对于所有的正整数n,2n+1均不能被7整除。
62.(1)设Tr+1=为常数项。
则有m(12-r)+nr=0,即m(12-r)-2mr=0,r=4,它是第5项。
(2)因为第5项是系数最大的项,故: