功欲善其事，必先利其器
——动点到定点距离最值问题的解题思路探析

张 淼

(浙江省余姚市实验学校 315400)

几何中动点到定点距离的最值问题，归根结蒂都是转化为两点之间线段最短，或直线外一点到直线上各点之间垂线段最短.但如何转化都大有文章，特别当动点所在图形未明示时，思维难度骤增，觉得毫无头绪，无从下手.为使距离最值问题的求解有图可索，有序可循，把它分门别类，加以探析.

一、动点在已知定直线上

动点在已知定直线上时，根据定点个数又分两类.

1.与两个定点有关

(1)当两个定点在定直线两旁时，直接运用两点之间线段最短，连结两定点的线段与定直线的交点即为所求.(当定直线改为定圆也同样)

(2)当两个定点在定直线同旁时，通过轴对称变换，作其中一个定点关于定直线的对称点，转化为(1)的情况.(此时定直线不能改为定圆)

例1 如图1，已知正方形ABCD，AB=a，E是AD上一定点，在AB上作出一点F，使以EF为一边的正方形ABCD的内接平行四边形EFGH周长最小，并求出最小周长.

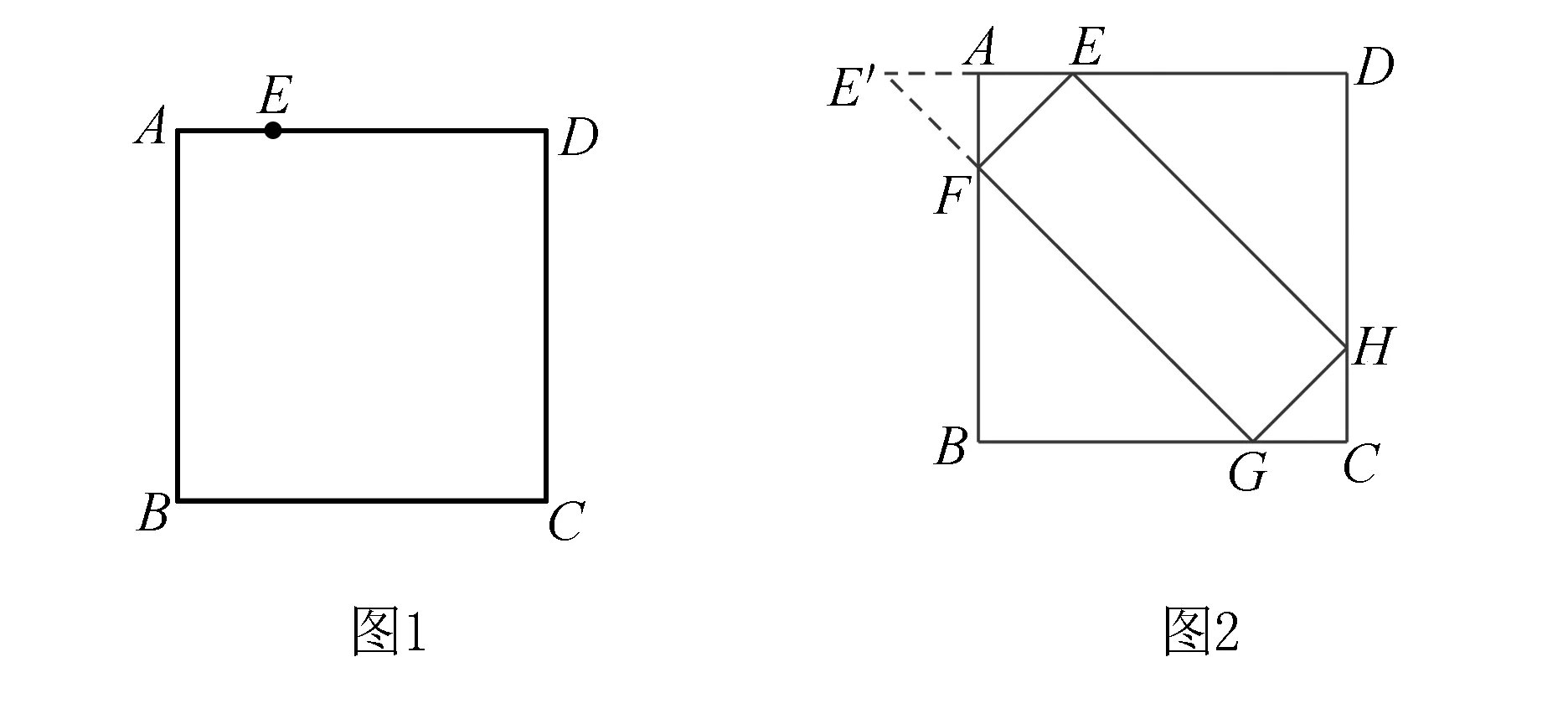
分析由正方形的对称性，既然EFGH是它的内接平行四边形，则顶点G必与顶点E关于正方形ABCD的对称中心对称，故点G可确定.

2.与一个定点有关

动点在定直线上与定直线外一个定点的最短距离，归结为直线外一点与直线上各点之间垂线段最短.具体求解时，往往要利用题中涉及的几何图形性质，以促使问题的转化.

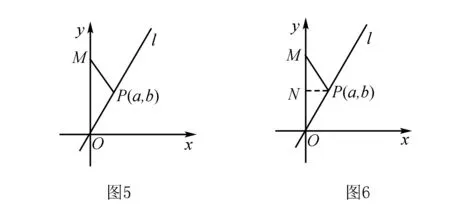
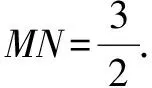
例4 如图7，在直角梯形ABCD中，AD=1，AB=2，BC=3，∠A=∠B=90°，E为AB上的动点，连结ED并延长至H，使DH=ED，以EH、EC为邻边作ECFH，求对角线EF的最小值.

二、动点在定圆上

当动点在定圆上时，应通过旋转变换或相似变换把问题归结为已知圆外一点到圆上动点距离的最值问题.

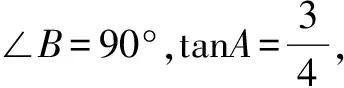
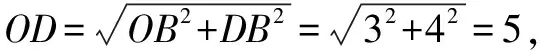
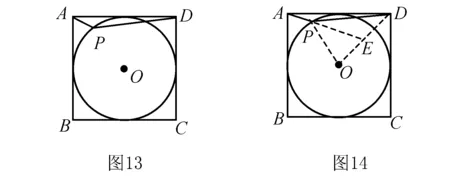
三、题设条件未明示动点所在图形

这类问题的求解，必须首先确定动点运动的轨迹是直线还是圆(弧)，然后再归结为上述两类求解.

例8 如图15，点A(0，6)，AB=BO，∠ABO=120°，点C在x轴上运动，在坐标平面内作点D，使△ACD∽△AOB，连结OD，求OD的最小值.

参考文献：

[1]潘小梅.初中数学典型问题100例[M].杭州：浙江教育出版社，2016(10).

[2]应立君，余雪赞.图形变换中蕴含的数学之美[J].实验苑,2016(5).