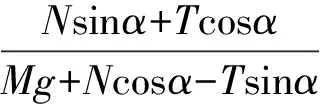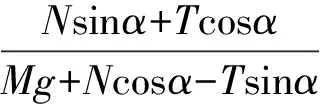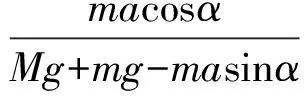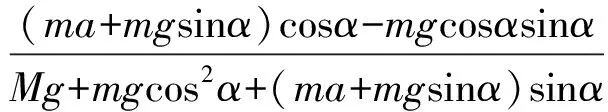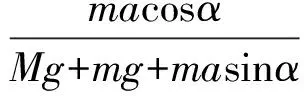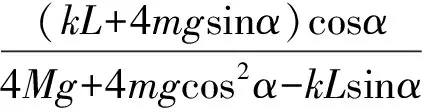基于一道高考题谈两种竞赛方法的运用

方 林 许新胜 陶士金

(1. 安徽师范大学物电学院,安徽 芜湖 241000; 2. 安徽省巢湖市第四中学,安徽 巢湖 238000; 3. 合肥市教科院物理教研室,安徽 合肥 230071)

基于一道高考题谈两种竞赛方法的运用

方 林1,2许新胜2陶士金3

(1. 安徽师范大学物电学院,安徽 芜湖 241000; 2. 安徽省巢湖市第四中学,安徽 巢湖 238000; 3. 合肥市教科院物理教研室,安徽 合肥 230071)

本文通过对一道高考题的另两种不同解法(即系统牛顿第二定律、摩擦角图解法)的归纳总结,以期达到拓宽对高考及竞赛题的解答思路及对其他力学问题的解答有启发作用的效果．

高考; 斜面; 加速度; 弹簧; 摩擦力

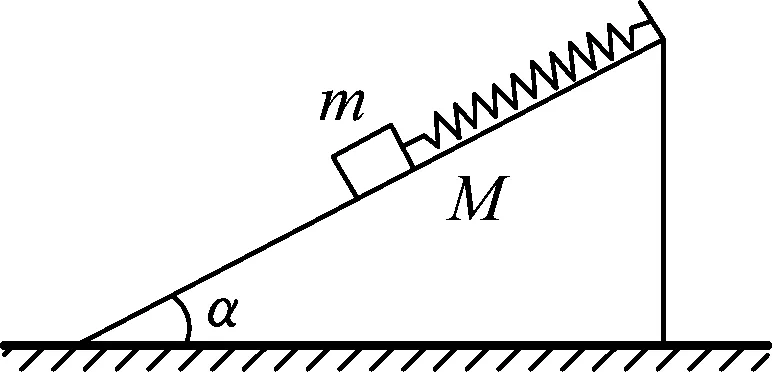
图1

(1) 求物块处于平衡位置时弹簧的长度;

(2) 选物块的平衡位置为坐标原点,沿斜面向下为正方向建立坐标轴,用x表示物块相对于平衡位置的位移,证明物块做简谐运动;

(3) 求弹簧的最大伸长量;

(4) 为使斜面体始终处于静止状态,动摩擦因数μ应满足什么条件(假设滑动摩擦力等于最大静摩擦力)?

由于本题主要难点在第(4)问,限于篇幅,我们略去前3问,重点剖析第(4)问的思路,给出另两种解法．

另解1(系统牛顿第二定律):

中学阶段运用牛顿第二定律解题时,研究对象往往选取单个物体或保持相对静止的几个物体所组成的整体．实际上,牛顿第二定律对几个有相对运动的物体所组成的系统(即质点组)也适用．系统牛顿第二定律的表达式为F外=m1a1+m2a2+m3a3+…+mnan,即系统受到的合外力等于系统内各物体的质量与其加速度乘积的矢量和.该式为矢量方程，可以在某一方向上列出分量式.

下面运用这种方法来处理第(4)小问．

根据物块实际运动特点,按物块的加速度沿斜面向下和向上两种情形分别进行讨论．

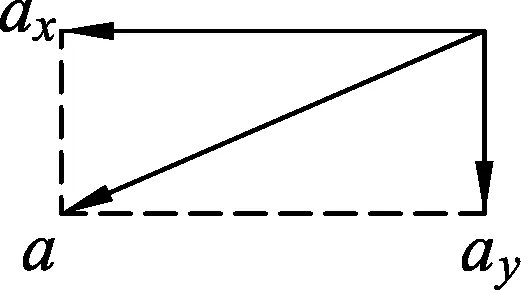
图2

如图2所示,当物块的加速度方向沿斜面体向下时,设物块运动时的加速度为a,可将其分解为水平向左的加速度ax和竖直向下的加速度ay,

则对系统,根据牛顿第二定律,

水平方向有f=max+M·0=macosα；

竖直方向有Mg+mg-FN=may+M·0=masinα.

而要使斜面体保持不动,需满足f≤fm=μFN,即μ(Mg+mg-may)≥max.

物块沿斜面体运动的加速度的最大值

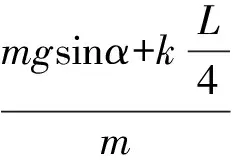
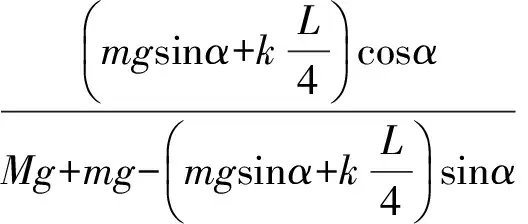
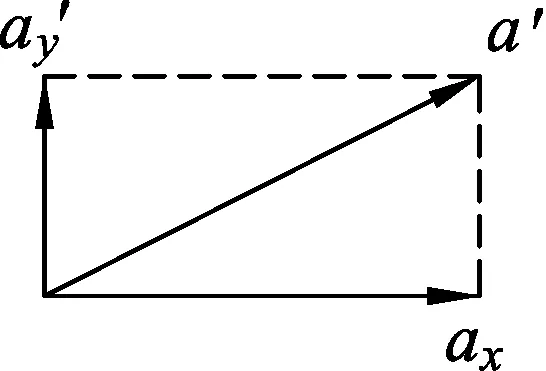
图3

如图3所示,当物块的加速度方向沿斜面体向上时,设此时的加速度为a′,现将其分解为水平向右的加速度ax′和竖直向上的加速度ay′,

则对系统,根据牛顿第二定律,

水平方向有f′=max′+M·0=ma′cosα

竖直方向有FN′-Mg+mg=may′+M·0=ma′sinα.

而要使斜面体保持不动,需满足f′≤fm′=μFN′,即μ(Mg+mg+may′)≥max′.

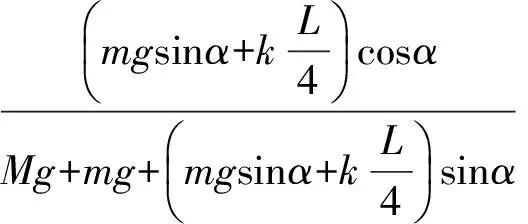
综合以上分析可知

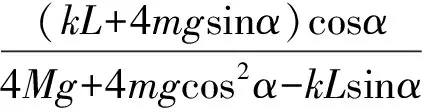
说明:运用系统牛顿第二定律来分析该问,打破了常规思路,巧妙地将有相对滑动的两个物体当成整体来研究,接着分别在水平和竖直方向对系统列出牛顿第二定律求解,这样就避开了用隔离法分析时所必需的物体间繁杂的受力分析．由此可见,当物体间受力较多或受力不清晰(如摩擦力方向不确定)时可以选系统作为研究对象来简化问题．

另解2(摩擦角):

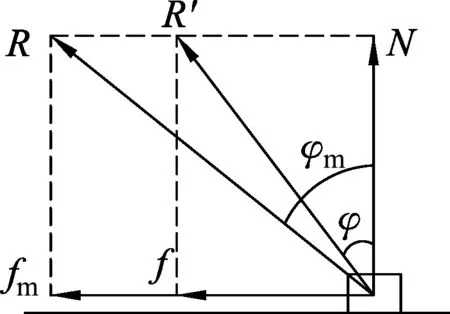
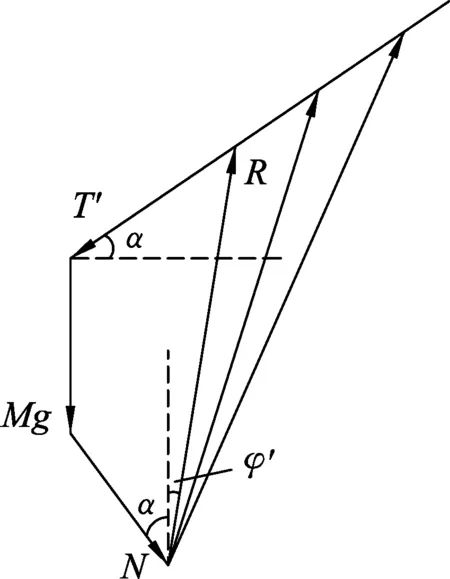
图4

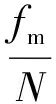
因静摩擦力0

本题第(4)问,也可以采用摩擦角知识结合图像法来分析．

下面按弹簧为压缩(图5)和拉伸(图6)两种情况分析第(4)问,分别作出斜面体的受力分析示意图如图5和图6,其中N为物块沿斜面运动时对斜面体的压力(为恒力),T为弹簧对斜面的作用力,R为地面施加于斜面的摩擦力f与支持力FN的合力,即全反力．对比分析图5和图6,不难发现,弹簧弹力越大,摩擦角φ(或φ′)就越大．

图5

图6

当弹簧被压缩时,根据平衡条件,对斜面,在竖直方向有Mg+Ncosα=Rcosφ+Tsinα,

水平方向有Rsinφ=Nsinα+Tcosα，

再隔离m,

沿斜面方向,由牛顿第二定律得

T+mgsinα=ma,

垂直斜面方向,由平衡条件得

N=mgcosα,

由题意,为使斜面始终处于静止状态,应满足f≤fm=μFN.

故动摩擦因数μ应满足μ≥tanφm.

弹簧拉伸时,根据平衡条件

对斜面,竖直方向有

Mg+Ncosα+T′sinα=Rcosφ′,

水平方向有

T′cosα=Nsinα+Rsinφ′，

再隔离m,

沿斜面方向,由牛顿第二定律得

T′-mgsinα=ma,

垂直斜面方向,由平衡条件得N=mgcosα,故

由上述分析可知,为使斜面始终处于静止状态,动摩擦因数μ应满足μ≥tanφm′.

综上,因tanφm>tanφm′,故

说明:在高中物理自主招生及竞赛时常会遇到相关摩擦的静力学问题,这类题的计算量往往比较大,相比常规思路而言(整体法、隔离法解题),运用摩擦角和全反力知识解题,将会有更大优势．

综上,对比两种不同方法,我们不难发现:系统牛顿第二定律的研究对象是物块和斜面体(含弹簧)组成的整体,这样就不用考虑物块和斜面体间的相互作用力(内力),只需考虑系统所受外力来分析问题了．而摩擦角法的研究对象是斜面体,虽然是用隔离法分析问题,但通过全反力的等效替代,减少了斜面体受力的个数,再作出斜面体的受力分析图(常见的为三角形,本题为多边形),就可以直观地找到临界状态,进而迅速求出对应受力的极值．

1 方林. 2014年安徽高考压轴题的三种不同解法[J].物理教学，2015(3):69-70.

2 方林.推陈出新,能力提升——对2013年安徽高考理综卷第20题的评析[J].物理教师，2013(12):73-74.

2017-04-12)