求最大公约数的两种算法案例

李彦峰

求最大公约数有两种经典算法，即辗转相除法与更相减损术。

一、辗转相除法

辗转相除法最早出现于公元300年的古-希腊作家欧几里得的《几何原本》中，也被称为欧几里得算法，其主要作用是求两个正整数的最大公约数。

辗转相除法的算理：对于给定的整数。和6，若a≥b，则a=qb+r，此时（a，b）=（b，r）。我们把整数a，b的最大公约数用记号（a，b）来表示，即a和b的最大公约数与b和r（r为a除以b的余數）的最大公约数是相等的。

用辗转相除法求两个正整数m，n（m>n）的最大公约数的步骤：

第1步，给定两个正整数m，n。

第2步，计算m除以n所得余数r。

第3步，m=n，n=r。

第4步，若r=0，则m，n的最大公约数等于m；否则返回第2步。

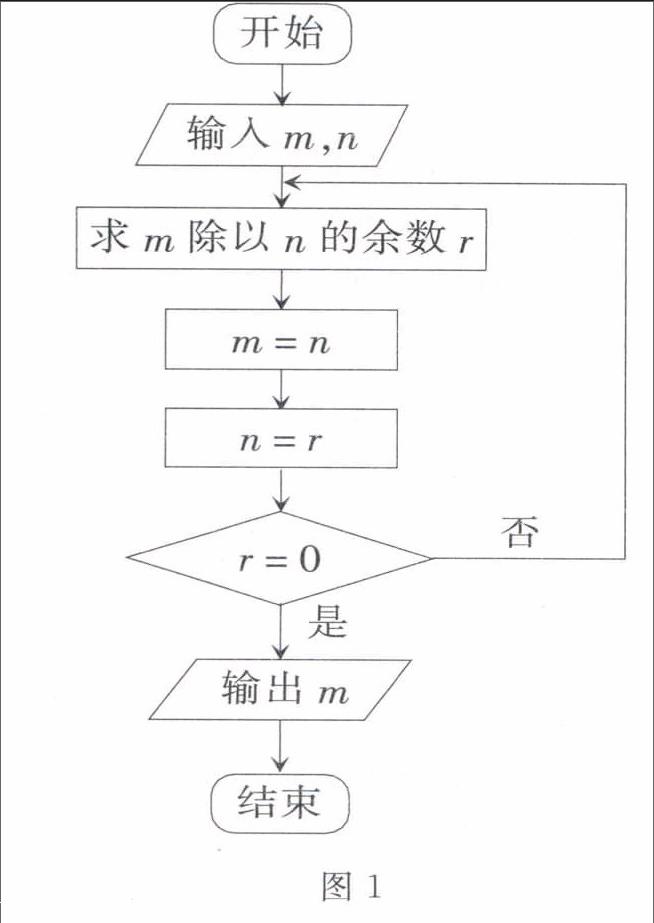
辗转相除法求最大公约数的程序框图如图1所示。

二、更相减损术

更相减损术是《九章算术》里的一种求两个正整数最大公约数的算法。

更相减损术求最大公约数的步骤：

第1步，任意给定两个正整数，判断它们是否都是偶数，若是偶数，用2约简；若不是偶数，执行第2步。

第2步，以较大的数减去较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的数相等为止，则这个数（等数）或这个数与约简的数的乘积就是所求的最大公约数。

更相减损术求最大公约数的程序框图如图2所示，其中m，n为正整数，且m，n都不是偶数。

如果m，n均为偶数，则先用2约简，直到不能同时用2约简为止，然后把约简所得的结果以较大的数减去较小的数进行辗转相减，得到“等数”。“等数”与约简的数的乘积就是所求的最大公约数。

（责任编辑 郭正华）