基于DEA方法的杨凌示范区科技创新绩效评价

（西北农林科技大学，陕西 杨凌 712100）

基于DEA方法的杨凌示范区科技创新绩效评价

冯梦涵，孔荣

（西北农林科技大学，陕西 杨凌 712100）

杨凌示范区作为国务院设立的中国唯一的农业高新技术产业示范区，正处于新一轮发展的关键时期。本文在分析区内科技创新现状以及投入产出的特点的基础上，建立一套科技创新绩效评估体系，运用DEA方法建立实证模型，评价杨凌示范区科技创新绩效，为示范区内科技创新工作的运行开展提供理论依据和决策支持。

科技创新；DEA；绩效评价

一、引言

国外学者对“科技创新”的研究较早且较为全面，其从技术创新和制度创新方面对“科技创新”进行了较为全面的研究。而国内学者对创新的研究较晚，在发展过程中需要跟随西方发达国家的步伐。国内学者对“科技创新”方面的研究主要集中在“自主创新”。近几年，大多数学者把技术创新能力、创新投入产出过程、技术创新阶段性作为研究方向，并在技术创新评价指标体系的设计上取得一定经验。目前科技创新绩效评价的研究大多针对某个行业和企业，而针对某个特定地区的研究很少。

杨凌示范区自1997年被国务院设立为农业高新技术产业示范区以来，科技发展迅速，科技自主创新能力不断提高，但仍然存在许多不足之处。例如，区内知识产权培训服务机构较少，企业的科技创新能力较弱，知识产权意识不强，科技创新成果高校居多而企业社会较少等。针对这些现象，当前迫切需要为杨凌示范区摸索构建一套科学合理、可操作性强的科技创新绩效评价方法，提出有针对性的实施科技创新驱动战略的合理路径。

二、科技创新绩效评价指标体系

科技创新是一个复杂的过程，其特点是具有众多投入和产出，因此，科技创新的实现与绩效评价是许多因素共同作用的结果。本文在分析整理相关文献的基础上，参照前人研究经验，结合杨凌农业高新技术产业示范区自身的特点，构建一套科技创新绩效评价指标体系，具体指标可以分为投入指标和产出指标。

投入指标包括人力投入和财力投入，具体可见以下四项：一是高新区企业数量：总体反映科技创新人力投入情况。二是教学与科研人员：从事高等学校教学、研究与发展、研究与发展成果及科技服务工作人员以及直接为上述工作服务的人员。此项代表科技创新人力整体投入情况。三是研究与发展人员：从事科学研究与实验发展工作占本人教学、科研总时间10%以上的教学与发展人员，直接反映科技创新的人力投入。四是R&D经费投入量：投入到科学研究与实验发展的费用总和，反映科技创新财力投入情况。

产出指标不仅表现为科学技术研究水平，还包括科技的转化能力。我们可以将其分为两类：一类是直接知识产出；另一类是科技转化经济产出。这两类指标能够全面反映科技创新的产出情况，综上选择以下产出指标。一是专利授权数：经国家知识产权局审批已经授权的专利数量，代表自主知识产权的拥有量。二是科技论文发表数：被各类期刊收录的论文数量，代表科技知识直接产出。三是出版科技著作数：公开出版发行的科技著作数量，代表科技知识直接产出。四是科技鉴定成果数：经科技部认定鉴定的科技项目数量，代表直接科技成果的拥有量。五是技术市场成交额：技术转让和出售专利所获得的总收入，反映科创新的直接经济产出。六是新产品销售收入：企业新产品的销售收入，能够从总量上反映科技创新成果的商业化和创新产品的市场化程度。七是高新技术产品产值：高新技术产品总产值，总体反映科技产出转化为经济产出的转化能力。八是高新区总工业产值：高新区总工业产值反映高新区工业企业工业生产的总体规模水平。

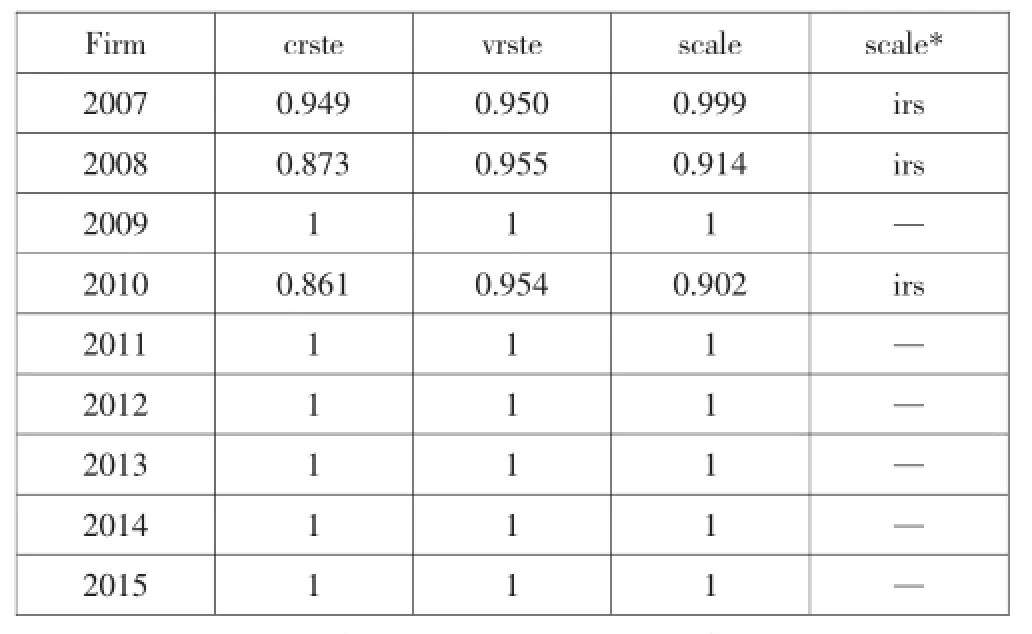
表1 DEA投入产出相对有效性评价结果

三、DEA方法原理

美国运筹学家Charnes和Coopor等人于1978年提出数据包络分析法，这是一种可以测评多输入、多输出的同类型评价单元相对效率的有效数量分析方法。它的原理是在保持评价单元的输入或输入不变的情况下，根据众多输入产出指标，通过统计规划确定相对有效的生产前沿面，从而将众多决策单元投影到DEA的生产前沿面上，最终对决策单元在生产前沿面的偏离程度进行比较，从而对各个决策单元的相对有效性做出有效评价。CCR和BCC模型都是DEA普遍应用的模型，BCC模型只评估规模有效，CCR模型可以评估技术有效和规模有效，进而计算出总效率值。本文选择CCR模型用来评价决策单元，CCR模型如下所示。

设有n个同类型的评价对象，即决策单元，每个决策单元由m种输入和s种输出组成。Xij代表第j个决策单元第i种输入指标的输入值，Yrj代表第j个决策单元的第r种输出指标的输出值。则第k个决策单元的效率可以用如下模型来表示：

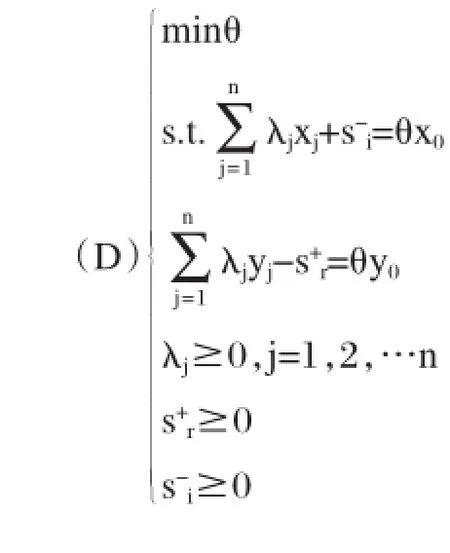
表2 DEA模型松弛变量结果

其中，s是松弛变量，θk是第k个单元的决策值，且满足0≤θk≤1。

我们利用该模型的结果就可以做出如下判断：

当θk＝1， 且 sk-i＝0，sk+r＝0时，则决策单元 jk为DEA有效，决策单元代表的经济活动同时达到了技术有效和规模收益。技术有效是指决策单元投入的资源得到了充分利用，达到最佳输出状态，投入产出平衡。规模有效指决策单元处于规模收益不变的理想状态。

当θk＝1，但至少存在某个输入值或者输出值大于0时，即至少有一个sk-i＞0，或至少有一个sk+r＞0，则称决策单元jk为弱DEA有效。若sk-i＞0，则表明第i种输入指标有sk-i的输入没有完全利用，也就是说相应的投入指标需要减少sk-i来使决策单元jk克服资源闲置；若某个sk+r＞0，则表示第r种输出单元比最大输出大sk+r的数量。

当θk＜1时，说明决策单元jk非DEA有效，即此项经济活动既未达到技术效率最佳，也不是规模收益的。说明决策单元jk的内部的运作效率较低，投入产出量不相匹配，存在较严重的资源浪费。

四、科技创新绩效实证研究

根据上文已经建立的指标体系，搜集相关数据并将数据带入CCR模型中，以杨凌示范区2007—2015年9个年度作为9个决策单元，运用DEAP2.1进行运算，结果如表1和表2所示。

表1的DEA基本模型评价结果显示，杨凌历年的投入产出绩效是基本有效的，除了2007、2008、2009这三年，其余年份综合效率值都等于1，松弛变量同时为0，说明这些年份是DEA有效的，即同时达到了技术效率最佳和规模收益；而2007、2008、2009这三年小于1，说明在这三年科技创新的投入产出存在失调，存在资源浪费和产出不足的现象，同时这三年的规模收益情况均处于递增状态，说明这三年的科技活动规模较小，还需要持续增加投入。通过分析表2中未达到DEA有效年份的松弛变量及其生产前沿面，可以得出这三年技术市场成交额的产出应该有较大幅度的提高，一般情况产出是我们不能决定的，因此我们考虑改变投入因素来提高其相对效率。

五、结论与建议

本文利用2007—2015年杨凌示范区科技创新相关统计数据，采用DEA中的CCR模型对其科技创新绩效进行评价。对评价结果进行分析后，我们可以得到以下结论：第一，总体来看，杨凌示范区历年创新绩效基本达到DEA相对有效，尤其是近五年以来都处于一个比较理想的状态；第二，没有达到相对有效的年份，都处于规模收益递增阶段，反映出其科技活动规模相对较小；第三，对松弛变量分析得出，产出未达到有效时，科技成果转让指标具有较大的提升空间，因此应该重点关注如何将科技成果转化为经济效益；第四，科技创新具有时间上的延迟性，某一年投入的加大可能并不能使当年的决策单元达到DEA有效，因此，投入量要在分析每年具体情况的基础上动态地制定不同的政策。

“十二五”以来，杨凌示范区在科技创新上处于一个比较理想的状态，同时达到技术效率最佳和规模收益，但依然有不足之处，为了更好地进展科技创新工作，提高区内科技创新效率，基于以上结论提出以下建议：第一，杨凌示范区在制定发展战略中，应继续加大科技资源的投入，加大R&D经费投资力度，大力支持技术含量较高、市场前景好的专利和项目，充分利用农科教育资源，加强校内科研团队与企业之间的合作，服务和支持区内科技型中小企业，注重提升企业自身的科技创新能力；第二，积极引进知识产权社会服务机构，定期为企业培训，提高企业的科技创新产权意识；第三，促进专利、著作、技术等的交易，大力促进科技成果的发布、交易与应用，加速科技成果的推广应用，最终将科技成果转化成经济产出。

[1] 吴文江：用数据包络分析研究规模收益分析[J].系统工程理论与实践，2001（9）.

[2] 张红辉、许继琴、刘尚海：基于DEA分析的宁波市科技自主创新绩效评价[J].科技进步与对策，2009（17）.

[3] 刘曙光、刘佳：区域创新系统研究的国内进展综述[J].经济师，2005（1）.

[4] 任胜钢、陈凤梅：国外区域创新系统研究新进展[J].外国经济与管理，2006（4）.

[5] 柳士双：国外区域创新体系研究新进展与启示[J].现代经济探讨，2012（4）.

[6] 李婷：基于DEA方法的西安高新区技术创新绩效评价研究[D].西安电子科技大学，2014.

[7] 支军、王忠辉：自主创新能力测度理论与评估指标体系构建[J].管理世界，2007（5）.

[8] 李宇、王俊倩：产业链垂直整合中的创新驱动与创新绩效研究[J].财经问题研究，2014（7）.

[9] John Phillimore.Beyond the linear view of innovation in science park evaluation-An analysis of Western Australian Technology Park[M].Murdoch University Murdoch，WA，Australia，1999.

[10] Chung Jen Chen，Chin Chen Huang.A multiple criteria evaluation of high-tech industries for the science-based industrial park in Taiwan[J].Information&Management，2004，41（7）.

[11] Fritsch M.Measuring the Quality of Regional Innovation Systems：A Knowledge Production Function Approach[DB]. http：//www.wiwi.tu-freiberg.de/wipol/pdffiles/ap200 l_2.pdf，2001-1.

[12] Riba Vilanova M.and Leydesdorff L.Why Catalonia CannotbeConsideredasaRegionalInnovationSystem[J].Scientometrics，2001，50（2）.

（责任编辑：刘冰冰）

杨凌示范区科学技术局项目，杨凌示范区科技创新：效率测度、绩效评估及策略选择，编号：2015RKX-09。