平面几何题两种解法的比较

江苏省通州实验中学(226300) 吴 健 ●

陕西省礼泉教研室(713200) 李 辉 ●

平面几何题两种解法的比较

江苏省通州实验中学(226300) 吴 健 ●

陕西省礼泉教研室(713200) 李 辉 ●

在中学阶段，平面几何题是教学的一个难点，如何解决这个难点?对这类问题主要有两个思路，一是从公理、定理、推论出发，通过推理得出结论;二是根据图形建立适当的坐标系，确定图形中已知点的坐标，灵活使用平面直角坐标系中的有关公式和方程来解决问题．

例1 在平面直角坐标系中，已知点A(4，0)，B(－6，0)，点C是y轴上的一个动点，当∠ACB=45°时，点C 的坐标为___．

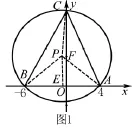
解法一 如图所示，根据题意可知，AB=10，线段AB的中点E的坐标为(－1，0)，过点E作EP⊥x轴且令，则△BPE和△APE都是等腰直角三角形，所以在△APB中，∠APB=90°．以点P为圆心，BP为半径作圆，与y轴交于点C，则∠ACB为弧所对应的圆周角，∠APB为弧所对应的圆心角，所以，故点C恰好在⊙P上．过点P作PF⊥y轴，则=OE=1，则在 Rt△CPF中，由勾股定理得 CF=，故OC=CF+OF=12，即点C的坐标为(0，12)．同理可得，当点C位于y轴负半轴时，点C的坐标为(0，－12)．

第一种解法是平面几何解法，需要添加辅助圆，用到圆周角定理和垂径定理，过程较为复杂;第二种解法设点的坐标，用到两角和的正切公式，较为简捷．

置，AD与AE在同一直线上，AB与AG在同一直线上．(1)求证:DG⊥BE;

(2)如图4，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，求此时BE的长;

(3)如图5，小明将正方形绕点A继续逆时针旋转，直线DG与直线BE相交于点H，求△AGH面积的最大值．

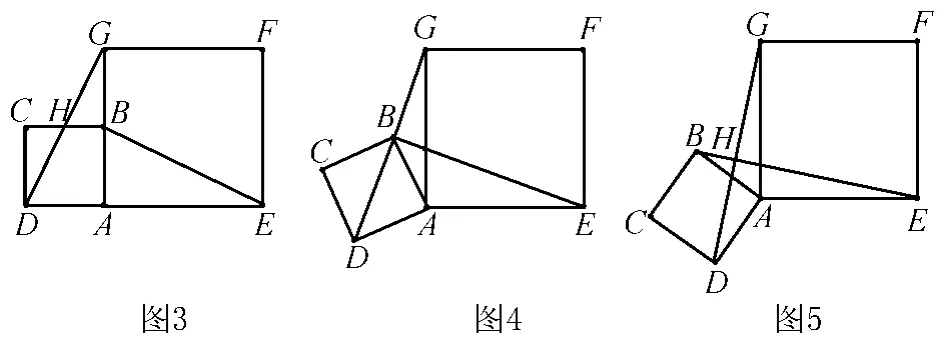
解法一 (1)证明:如图10所示，延长EB交DG于点H．因为四边形ABCD与四边形AEFG是正方形，故在△ADG和△ABE中，由，得△ADG≅ ABE(SAS)，所以∠AGD=∠AEB，在△ADG中，∠AGD+∠ADG=90°．所以∠AEB+∠ADG=90°．在△DHE中，根据三角形内角和为180°，所以∠DHE=180°－90°=90°，所以DG⊥BE．，所以△ADG≅△ABE(SAS)，所以DG= BE．因为BD为正方形对角线，所以∠MDA=45°．因为∠AMD=∠AMG=90°，所以△AMD为等腰直角三角形，

(2)如图11所示，作AM⊥DG交DG于点M．因为∠DAB=∠GAE，所以∠DAB+∠BAG=∠EAG+∠BAG，即 ∠DAG = ∠BAE，故 在 △ADG 和 △ABE 中，AD=AB，所以DM=AM=1．在Rt△GMA中，所以

(3)点H在以EG为直径的圆上，是一个定圆，同时H在以BD为直径的圆上，是一个动圆，其运动区域是以A为圆心，以AC为半径的圆内部区域．由图形可知当H点与C点重合时，H点离AG的距离最大，从而△AGH的面积最大．在Rt△ADG中，所以DG=中，AG边上的高为，所以△AGH的最大面积为

解法二 (1)以A点为坐标原点，AE所在直线为x轴，建立直角坐标系，则，得

(2)以A点为坐标原点，AE所在直线为x轴，建立直角坐标系，则设正方形ABCD绕点A逆时针方向旋转的角度为θ，则B点坐标为即点坐标为即(．因为B点在直线DG上，所以kDG，即，化简得cosθ－sinθ由sin2θ+cos2θ=1解得负值舍去得

第一种解法是平面几何法，用到三角形全等和圆的相关知识;第二种解法是建立直角坐标系，利用斜率和两点间距离公式，还有轨迹方程及用导数求最值，运算量极大．

从这两个例子可以看出，两种解法各有特点，例1用第二种方法解较简单，例2用第一种解法较简单．平面几何解法需要添辅助线，需要一定的技巧，坐标法的思想促使人们运用各种代数的方法解决几何问题．很多几何中的难题，一旦运用代数方法后就变得平淡无奇，但同时，也增加了解决问题的运算量．

G632

B

1008－0333(2017)02－0036－02