基于压缩感知的盲源信号分离检测方法

杨 挺，尚 昆，袁 博，张燕萍，盆海波



基于压缩感知的盲源信号分离检测方法

杨 挺1，尚 昆1，袁 博2，张燕萍3，盆海波1

(1. 天津大学智能电网教育部重点实验室，天津 300072；2. 国网河北省电力公司经济技术研究院，石家庄 050000；3. 国网天津市电力公司培训中心，天津300181)

接入电网的各种分布式电源、非线性负荷使得电能质量污染问题日益严重，对各种电能质量信号进行特征提取与正确分离是改善电能质量的切入点．针对电能质量信号的结构特点，构建了压缩感知电能质量信号分离模型，并针对该模型提出一种基于压缩感知的盲源信号分离检测算法CS-SCA(compressed sensing-sparse component analysis)．根据已有的电能质量信号理论知识，确定电能质量信号在频域的稀疏性，进而对信号预处理降噪．通过两步法解决预处理后电能质量观测信号的分离检测问题．第1步通过观测信号向量方向特性估计出电能质量源信号个数，并利用线性聚类估计混合矩阵；第2步采用压缩感知恢复算法分离得出电能质量源信号．通过实验验证，提出算法所分离出基波、各次谐波信号分离信干比均大于10,dB．

电能质量信号；压缩感知；稀疏成分分析；盲分离

随着智能电网的不断发展，接入电网的各种分布式电源、非线性负荷等使电能质量污染问题日益严重，电能质量监测是治理和改善电能质量的前提[1].电能质量监测除具有检测功能，还应具有分析功能.对各种电能质量信号进行特征提取与正确分离则是采取适当措施改善电能质量的切入点．

目前，学者们对电能质量信号分离检测进行了大量研究．文献[2]基于Desirable Sidelobe窗快速傅里叶变换进行电力系统谐波分析．文献[3-4]提出用最小二乘支持向量机及基于S变换和动力学的混合方法对电能质量信号进行检测、分类等研究．针对传统方法存在一定的频谱泄漏及存储数据量大等问题，盲源信号分离技术被提出并用以进行信号分离[5-7]，文献[5]提出一种势函数欠定盲源分离算法实现源信号个数及混合矩阵的估计．文献[6]将势函数及压缩感知理论结合起来研究音频信号的欠定盲分离方法，但由于未能充分利用信号本身特性，其估计出的混叠矩阵精度和鲁棒性存在不足．

电力系统中电能质量信号包含基波、谐波和扰动信号．常见的电能质量扰动有暂降、暂升、中断、闪变、暂态振荡、暂态脉冲、尖峰、缺口．根据电能质量信号的组成特点及已有的电能质量信号相关理论知识，电能质量信号在频域有很好的稀疏性．本文将压缩感知理论引入到欠定盲源分离恢复过程中，构建了压缩感知电能质量信号分离模型，并针对该模型提出一种基于压缩感知的盲源信号分离检测算法CS-SCA(compressed sensing-sparse component analysis)．首先对路电能质量观测信号进行预处理降噪，进而对预处理后的电能质量信号利用两步法进行电能质量信号盲源分离．第1步，在估计出电能质量源信号个数的基础上，利用线性聚类估计混合矩阵；第2步，采用压缩感知恢复方法分离出各源信号．对无噪声和含噪声两种电能质量观测信号进行实验验证，所提出算法估计源信号数目精度为100%,，分离各源信号的信干比SIR＞10,dB，表明CS-SCA可实现电能质量源信号有效分离．

1 压缩感知盲信号分离模型

1.1 压缩感知理论

压缩感知(compressed sensing，CS)是一种新型的信号采样理论[8]，当信号满足稀疏性条件时，可以将信号投影到低维空间以远低于信号Nyquist频率的采样速率对信号进行全局观测，然后通过合适的恢复算法重构源信号．压缩感知理论突破了Nyquist采样定理的瓶颈，建立了全新的信号描述和处理框架，极大地降低数据采集——传输量和处理成本，降低计算量，减少计算时间．压缩感知理论将压缩过程与采样过程相融合，在采样中完成对数据的压缩，有效降低对采样端对硬件的需求．

压缩感知理论核心思想是：当维原始信号为稀疏信号时，通过测量矩阵对进行线性降维观测得到维观测向量(＜)，称为压缩采样值，然后利用压缩感知恢复算法重构出稀疏向量和原始信号．其模型为

   (1)

1.2 盲源信号分离基本原理

盲源信号分离(blind signal separation，BSS)[9]检测技术可在源信号和传输信道参数均未知的情况下，根据源信号的统计特性，仅通过从传感器获取的混合信号和少量的先验信息恢复出源信号的过程，故采用盲信号处理技术的谐波检测方法更具有实用价值与理论意义．盲信号分离的核心问题是分离矩阵的学习算法．

盲源分离基本思想是维未知源信号()及维噪声()经未知混合矩阵得到维观测信号()．求分离矩阵，使得通过该矩阵就可从观测信号()恢复出源信号()，盲源分离的数学模型可表示为

   (2)

实际BSS问题根据和的关系分为3类：

(1)＞，观测信号的个数大于源信号的个数(超定盲源分离问题)；

(2)＝，观测信号的个数等于源信号的个数(正定盲源分离问题)；

(3)＜，观测信号的个数小于源信号的个数(欠定盲源分离问题)．

1.3 压缩感知盲源信号分离模型

欠定盲源信号分离模型和压缩感知理论模型二者都是求解欠定方程组的问题．将欠定盲源信号分离模型中的混合矩阵与压缩感知理论模型中的测量矩阵对应，观测信号()与测量向量对应，则可在压缩感知框架下求解欠定盲源信号分离模型．

   (3)

则欠定盲源信号分离问题就可以通过求解最小0范数的最优化问题来实现，即

   (4)

综上分析，欠定盲源分离问题表示为给定观测信号()和观测矩阵，寻找源信号()，使得，且()在稀疏基的作用下，源信号分离问题可以通过压缩感知理论中的信号恢复算法来解决．与压缩感知信号重构过程所不同的是，在欠定盲源信号分离问题中，由于混合矩阵是未知的，因此求解式(4)还需要预先估计出混合矩阵．

2 电能质量信号分离检测

2.1 电能质量信号稀疏性

信号的稀疏性是压缩感知盲信号分离模型继续研究的前提，稀疏信号是指在绝大多数时刻取值为零或者小，在少数时刻取值比较明显的信号．

文献[11]给出了基波、谐波及各类扰动信号的公式及波形，由于电能质量的各类信号在时域不符合稀疏信号特征，文献[12]对电能质量信号进行时-频域转换，发现电能质量信号在频域内表现出少量大系数值和大量的近似为零值的特性，满足信号的稀疏性特征.

2.2 基于压缩感知电能质量信号分离模型

根据电能质量信号的稀疏性分析，监测信号中含有基波、谐波以及电能质量扰动信号，且具有稀疏性．本文所求解的问题如下．

在已知电能质量信号相关理论知识以及观测信号，采用压缩感知电能质量信号分离模型分解出检测电能质量信号的各个组成部分．

电能质量信号欠定盲分离表示为

   (5)

式中：x为第个观测信号；a为混合矩阵的系数；s为第个源信号．针对具体电能质量信号各个采样点，式(5)可改写为

   (6)

式中为以a为值的×对角矩阵．

通过压缩感知盲源信号分离模型可知，该欠定盲源信号分离问题就可以通过式(4)中求解最小0范数来实现．

2.3 基于压缩感知电能质量信号分离算法

本文将电能质量信号分析问题转换为电能质量信号欠定盲源分离问题，此外，为减少采样端海量存储和数据传输压力，本文将压缩感知理论引入到欠定盲源分离恢复过程中，并针对该压缩感知盲源分离模型提出一种CS-SCA算法．

CS-SCA算法采用两步法进行电能质量信号分离：第1步估计混合矩阵；第2步恢复源信号．由于现实中观测信号往往存在大量噪声，如果直接进行盲信号分离的话就会导致分离效果不佳，甚至无法分离．这就要求对信号进行降噪处理，实现信号的精确分离．本文增加对观测信号进行中心化和白化处理来抑制噪声、使信号具备统计独立性，从而达到提高分离精度的目的．预处理电能质量信号后，通过电能质量观测信号向量方向特性，估计出源信号数目．进一步通过源信号的数目对观测信号线性聚类估计混合矩阵．聚类的类别数等于估计出的源信号的个数．在估计出混合矩阵的前提下，应用压缩感知恢复算法CoSaMP[13]分离出各源信号．

CoSaMP是一种高精度的信号重建算法，在采样过程中对噪声有很强的鲁棒性．其中，本文采用傅里叶变换基稀疏进行稀疏化，因此可以确定每个谐波分量的稀疏度＝2，总稀疏度＝2,．CS-SCA算法流程如图1所示.

图1 CS-SCA算法流程

3 实验分析

为验证本文所提出的方法对混合电能质量信号的分离检测效果，结合电力系统电能质量信号的特点，本文对两路电能质量信号(以电压为例)进行盲分离实验，如表1所示．并分别对无噪声及含有噪声两种场景进行实验．

表1 电能质量观测信号

Tab.1 Power quality observation signals

CS-SCA算法通过估计方法得到估计混合矩阵，为了衡量估计矩阵的精确性，文中采用广义串扰误差(generalized cross-talking error，GCE)的误差衡量标准[14]进行判定．分离算法性能评价采用信号-干扰比(signal-to-interference-ratios，SIR)，简称信干比[15].本文采用该评价指标对所提出算法进行性能评测．评价指标分别定义为

   (7)

   (8)

3.1 源信号个数估计性能分析

1) 无噪声场景下

在无噪声场景下，表1两路电能质量观测信号波形如图2所示．

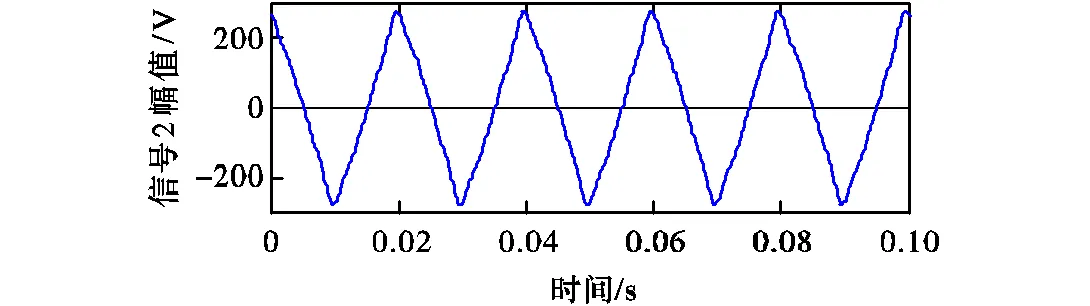
图2 无噪声混合电能质量信号时域图

源信号数目估计实验结果如图3所示，除零点外，图中信号集中在4个点附近，形成4个分离的向量，由此清晰获得源信号中包含4个分量．

2) 含噪声()≠0(SNR＝30,dB)场景下

在含有干扰噪声且信噪比为30,dB的场景下，表1两路电能质量观测信号波形如图4所示，由于受噪声干扰，可观测波形中含有大量毛刺．

图5给出源信号数目估计实验结果，在信号时频域散点图上，非零值数据明显分散在4个方向向量上，可准确确定源信号个数为4，源信号估计准确度100%,．

3.2 混合矩阵估计性能分析

采用本方法中线性聚类估计出混合矩阵如表2所示．计算估计混合矩阵GCE值，其中本文估计的混合矩阵在含噪声场景下的GCE＝0.25，在不含噪声的干扰下混合矩阵估计值与实际值完全相同，即GCE＝0．实验结果表明本文提出算法在有无噪声场景下均可准确地估计出混合矩阵．

表2 估计混合矩阵

Tab.2 Estimated mixing matrix

3.3 源信号分离检测性能分析

1)无噪声场景下

采用本文方法中压缩感知分离得到的电能质量源信号如图6所示．

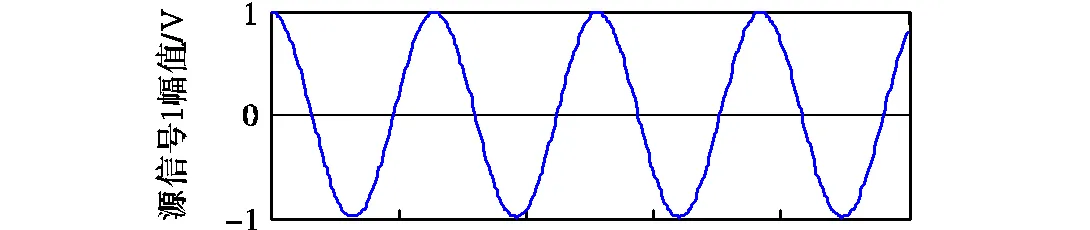
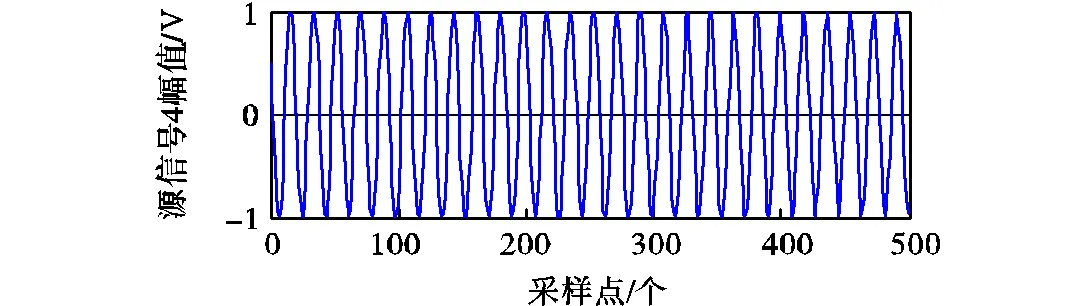
图6 电能质量源信号图(无噪声)

2)含噪声()≠0(SNR＝30,dB)场景下

在存在信噪比为30,dB干扰噪声情况下，使用本方法分离得到的电能质量源信号如图7所示.

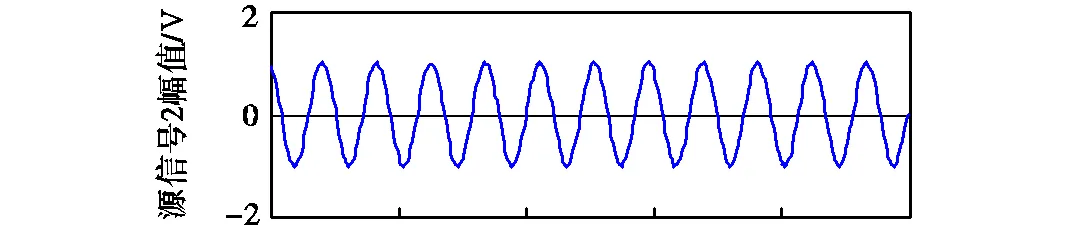
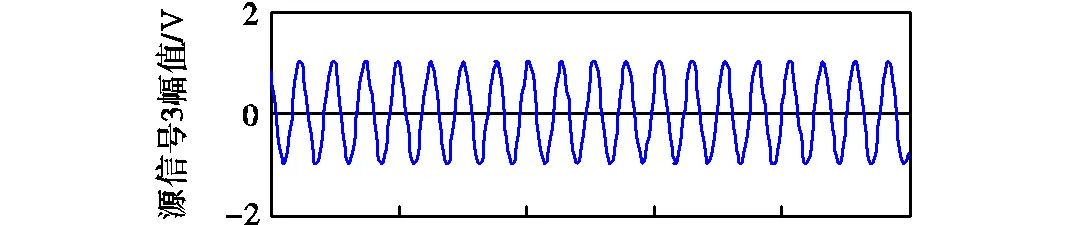
图7 电能质量源信号图(SNR=30 dB)

利用式(8)计算本方法获得各源信号的SIR．两种情况下得到各源信号SIR如表3所示．

表3 源信号的信干比

Tab.3 SIR of source signals

在盲源分离问题中认为SIR＞10,dB，源信号得以有效分离．仿真结果表明，即使在含噪干扰的场景下，本文方法也能很好地分离各次谐波信号，满足分离各个电能质量信号的要求．

4 结 语

接入电网的各种分布式电源、非线性负荷等使得电能质量污染问题日益严重，对各种电能质量信号进行特征提取与正确分离是改善电能质量的切入点．本文根据实际电能质量信号的结构组成特点，首先通过时频域转换分析电能质量信号所包含的基波、谐波、电能质量扰动信号的稀疏性．基于电能质量信号频域稀疏性，本文将电能质量信号分析问题建模成欠定盲源分离模型，并针对该模型提出一种CS-SCA算法．该算法通过线性聚类估计出混合矩阵，压缩感知恢复算法分离出各源信号．通过仿真验证本文所提出的CS-SCA算法的有效性，结果得出各个电能质量源信号分离SIR均大于10,dB，表明本方法能够准确分离检测出各个电能质量源信号，为进一步电能质量信号分析提供保障．

［1］ 王继东，秦美翠. 基于单周控制有源电力滤波器的微网谐波抑制方法[J]. 天津大学学报：自然科学与工程技术版，2015，48(7)：637-642.

Wang Jidong，Qin Meicui. Micro-grid harmonic suppression method based on one cycle controlled active power filter[J].：，2015，48(7)：637-642(in Chinese).

［2］ Wen H，Teng Z，Wang Y，et al. Spectral correction approach based on desirable sidelobe window for harmonic analysis of industrial power system[J].，2013(3)：1001-1010.

［3］ 秦 业，袁海文，袁海斌，等. 基于优化最小二乘支持向量机的电能质量扰动分类[J]. 电工技术学报，2012，27(8)：209-214.

Qin Ye，Yuan Haiwen，Yuan Haibin，et al. Classification of power quality disturbances based on optimized least squares support vector machine[J].，2012，27(8)：209-214(in Chinese).

［4］ He S，Li K，Zhang M. A real-time power quality disturbances classification using hybrid method based on S-transform and dynamics[J].，2013，62(9)：2465-2475.

［5］ 付卫红，王 璐，马丽芬. 一种改进的势函数欠定盲源分离算法[J]. 西安电子科技大学学报：自然科学版，2014，41(6)：1-5. Fu Weihong，Wang Lu，Ma Lifen. Improved Laplace mixed model potential function algorithm for UBSS[J].：，2014，41(6)：1-5(in Chinese).

［6］ 李丽娜，曾庆勋，甘晓晔，等. 基于势函数与压缩感知的欠定盲源分离[J]. 计算机应用，2014，34(3)：658-662.

Li Lina，Zeng Qingxun，Gan Xiaoye，et al. Under-determined blind source separation based on potential function and compressive sensing[J].，2014，34(3)：658-662(in Chinese).

［7］ Liu J，Yu F，Chen Y.[M]. Germany：Springer International Publishing，2014：43-50.

［8］ Donoho D L. Compressed sensing[J].，2006，52(4)：1289-1306.

［9］ Der B R. Blind signal separation[J].，2010，13(3)：248-250.

［10］ Blumensath T，Davies M. Compressed sensing and source separation[C]//. Heidelberg，Germany，2007：341-348.

［11］ Sánchez P，Montoya F G，Manzano-Agugliaro F，et al. Genetic algorithm for S-transform optimisation in the analysis and classification of electrical signal perturbations[J].，2013，40(17)：6766-6777.

［12］ Shen Y，Zhang H W，Liu G H，et al. Power quality data compression based on sparse representation and compressed sensing[C]//2014 11(). Shenyang，China，2014：5561-5566.

［13］ Needell D，Tropp J A. CoSaMP：Iterative signal recovery from incomplete and inaccurate samples[J].，2009，26(3)：301-321.

［14］ Theis F J，Lang E W，Puntonet C G. A geometric algorithm for overcomplete linear ICA[J].，2004，56：381-398.

［15］ Reju V G，Koh S N，Soon Y. An algorithm for mixing matrix estimation in instantaneous blind source separation[J].，2009，89(9)：1762-1773.

(责任编辑：孙立华)

Blind Signal Separation Detection Method Based on Compressed Sensing

Yang Ting1，Shang Kun1，Yuan Bo2，Zhang Yanping3，Pen Haibo1

(1．Key Laboratory of Smart Grid of Ministry of Education，Tianjin University，Tianjin 300072，China；2．State Grid Hebei Electric Power Company Economic Research Institute，Shijiazhuang 050000，China；3. Training Centre of State Grid Tianjin Electric Power Corporation，Tianjin 300181，China)

Large numbers of distributed generations and non-linear loads make the power quality environment increasingly complex．How to feature extract and separate all kinds of power quality signals have become the key to improving the power quality．Based on the characteristics of power quality signals，this paper established the underdetermined blind source separation model，analyzed the similarities in basic mathematical model between compressed sensing(CS)and blind source separation(BSS)，and then proposed a novel compressed sensing-sparse component analysis algorithm CS-SCA．Firstly，the sparsity of power quality signals was obtained by the time-frequency domain analysis，and then each of the observed signals was preprocessed to reduce the noise．Two-step CS-SCA was presented to achieve the power quality signals source separation．In the first step，the mixing matrix was estimated using linear clustering based on the estimation of the number of source signals through the direction characteristics of observed signals vector．In the second step，a CS reconstruction algorithm was used to separate the power quality source signals．The simulation results show that the SIR(signal-to-interference-ratio)of fundamental and harmonic components is higher than 10,dB，which proves that the proposed method can effectively separate each power quality source signal.

power quality signal；compressed sensing；sparse component analysis；blind separation

10.11784/tdxbz201512031

TM73；TP393

A

0493-2137(2016)11-1138-06

2015-12-08；

2016-03-29.

国际科技合作专项资助项目(2013DFA11040)；国家自然科学基金资助项目(61571324)；国家高技术研究发展计划(863计划)资助项目(2015AA050202)；天津市自然科学基金重点资助项目(16JCZDJC30900).

杨 挺（1979—  ），男，博士，教授，博士生导师．

杨 挺，yangting@tju．edu．cn.