空中的水龙头
江苏省常熟市外国语初级中学八(1313)班 赵筱薇
空中的水龙头
江苏省常熟市外国语初级中学八(1313)班 赵筱薇

这次春游,我们去了上海科技馆参观,展馆里面有着许多新奇的事物:倾斜的房间、鱼洗、三维动态成像、电磁炮……其中,我认为最引人注目的是悬于空中的水龙头.其实这个设施的结构很简单,在水龙头下方有一根透明管子支撑着它,而周围的水流又恰好挡住了这根管子,于是给人一种“天上水”的错觉.那么在数学中是否也有这样的“天上水”呢?我想到了曾经遇到的这样一个问题:
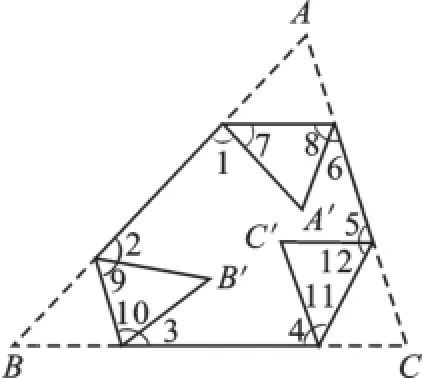
图1
如图1,把三角形纸片ABC的3个顶点进行折叠,折叠后3个顶点没有重合,求∠1+∠2+∠3+∠4+∠5+∠6的值.
这六个角看起来毫无联系,怎么办呢?
对于几何问题中的角度求解,我们常选择两种途径进行解决:利用内角或外角.
以内角为例,虽然题目不曾提到过,但显然三角形纸片满足“三角形的内角和为180°”.这根“透明管子”很好找,用手轻轻一碰即可触摸到.因为折叠的关系,所以可得出∠A=∠A′,∠B=∠B′,∠C=∠C′.于是等量代换后可得到∠A′+∠B′+∠C′=180°.通过观察可发现:∠7、∠8、∠9、∠10、∠11、∠12与∠A′、∠B′、∠C′恰好为三个三角形的九个内角,同时这六个角与∠1、∠2、∠3、∠4、∠5、∠6的有机组合又恰好构成一个六边形的六个内角,则问题便迎刃而解.解答如下:
因为∠A+∠B+∠C=180°,且∠A=∠A′,∠B=∠B′,∠C=∠C′,
所以∠A′+∠B′+∠C′=180°,
而∠A′+∠7+∠8=180°,
∠B′+∠9+∠10=180°,
∠C′+∠11+∠12=180°,
所以∠7+∠8+∠9+∠10+∠11+∠12=540°-(∠A′+∠B′+∠C′)=360°.
因为六边形的内角和为720°,
故∠1+∠2+∠3+∠4+∠5+∠6=720°-(∠7+∠8+∠9+∠10+∠11+∠12)=360°.
其实,“透明管子”在数学学习中随处可见,它就是问题的隐含条件.如果我们能好好利用这些条件,那么解题就会变得更加简单快捷,我们就能够创造出属于自己的“天上水”了!
教师点评:利用隐含条件解题是近年来各类考试包括中考中的热点问题.所谓隐含条件,就是在题目中未明确表达出来而客观上已存在的条件.数学中的隐含条件往往是解决问题的关键,这些条件容易被大家忽视.赵同学从去上海科技馆的一次社会实践活动中的所见所闻联想到了数学中的“天上水”,表明小赵注重生活与数学的联系,善于挖掘问题中的隐含条件,从而顺利解题.审题时,同学们应多揣摩、多思考,不能只看表象,应思考题设可能的衍生线路.解题时,同学们可从概念特征、数式特征、图形特征等方面对隐含条件进行挖掘,逐渐寻找到问题的本质.
(指导教师:张文明)

