考虑市场竞争条件的新建物流中心选址问题研究

李　蕾，郑鹏杰

（1.青海交通职业技术学院　管理工程系，青海　西宁　810003；2.中铁第四勘察设计院集团有限公司　线站处，湖北　武汉　430063）



考虑市场竞争条件的新建物流中心选址问题研究

李蕾1，郑鹏杰2

（1.青海交通职业技术学院管理工程系，青海西宁810003；2.中铁第四勘察设计院集团有限公司线站处，湖北武汉430063）

在市场竞争条件下，提出了新建物流中心的选址模型与算法，考虑原有物流中心的竞争，建立了基于市场竞争的新建物流中心选址双层规划模型，上层规划为新建物流中心的总成本最小，下层规划为客户选择最优且总费用最小。根据模型的特点，设计了一种基于Frank-Wolfe算法和遗传算法相结合的迭代算法对其进行求解。最后，通过算例分析验证了模型和算法的有效性，为新建物流中心选址提供了科学的决策方法。

物流中心；市场竞争；双层规划；遗传算法；Frank-Wolfe算法；选址

1　引言

随着现代物流的快速发展，对物流中心的功能与数量提出了更高的要求，原有的一些物流中心不能满足现代物流发展需求，新建物流中心是现代物流发展的必要途径。新建物流中心选址是一个复杂的系统工程，在原有物流中心基础上，需要考虑与原有物流中心的竞争，所谓的竞争主要是指与原物流中心共同负责客户的配送任务。

对于物流中心的选址问题，国内外研究已颇为成熟。物流中心选址最先使用的方法是重心法和物流位图法，重心法是根据物理学原理，在平面中找到图形的重心来确定物流中心的地址［1］。而物流位图法是通过模拟流体力学的“位势”来确定物流中心的地址［2］，重心法理论上可行，但难以在实际中实现，物流位图法计算复杂性较大，运算比较麻烦。随着计算机技术的不断发展，物流中心选址方法也不断完善，不确定规划方法和双层规划方法等在物流中心选址中得到较好的应用，文献［3］提出在不确定条件下，建立了随机规划选址模型，并给出了模型的鲁棒性优化，Schuetz等提出用户需求和短期成本都是随机变量的物流中心选址模型，并运用拉格朗日方法进行求解［4］。文献［5-6］运用GIS技术对多级物流中心动态选址问题进行了研究，文献［7-8］运用双层规划模型研究了供应链选址问题，并提出双层规划模型更能系统的分析选址过程。

综上所述，国内外研究学者在物流中心选址问题上研究较为丰富，但都是笼统的考虑物流中心选址，没有进一步深入地研究物流中心选址的影响因素，尤其原有物流中心对于新建物流中心的竞争尤为重要，基于此，在市场竞争条件下，本文对新建物流中心选址问题考虑市场竞争因素，建立基于市场竞争的新建物流中心选址模型，并设计合理算法进行求解。

2　问题分析

考虑市场竞争条件下的新建物流中心选址就是将原有的物流中心和新建物流中心一起研究，不仅考虑原有物流中心的运输费用，而且还考虑与新建物流中心的运量分担，原有的物流中心对新建物流中心产生较大影响，新建物流中心选址问题如图1所示。在已有物流中心1的前提下，如何选择在2或3处新建物流中心，考虑所有的客户需求全部满足。

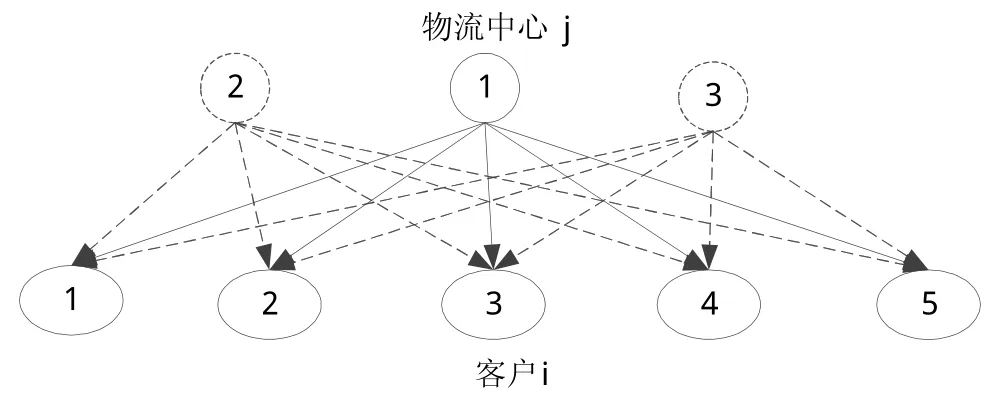
图1　新建物流中心选址问题分析

3　数学模型

3.1符号及参数定义

为研究方便，定义本文模型所需符号与参数如下：A=A1⋃A2表示所有物流中心的集合，包括原有物流中心和备选新建物流中心，其中A1=｛j：j=1,2,…,n｝表示原有物流中心的集合，A2=｛j：j=n+1,n+2,…,n+m｝表示备选新建物流中心集合；B=｛i：i=1,2,…,k｝表示所有物流中心覆盖的客户集合；cij表示第i个客户由第 j个物流中心提供运输服务的单位广义费用；xij表示第i个客户在 j物流中心满足的运输量；fj表示在 j地点新建物流中心的固定投资，j∈A2；δj为0-1变量，在j（j∈A2）处新建时等于1，否则为0；Wi表示第i个客户的总运输需求量；R表示一个充分大的正数。

3.2上层模型

（1）目标函数。上层目标考虑到决策部门的利益，必须在决策部门投入成本允许的范围内进行新建物流中心最优选址，使得新建物流中心总成本最小，包括固定成本和变动成本，得到目标函数如下：

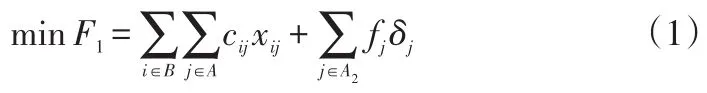
（2）约束条件。由于考虑到新建物流中心的必要性，故至少需要新建一个物流中心，得到约束条件如下：

一般情况下，决策部门在建设物流中心之前会有预算（N0），故必须在预算内进行，可得约束条件如下：

δj是一个0-1变量，约束如下：

3.3下层模型

（1）目标函数。下层模型表示多个物流中心竞争条件下，所有客户需求量在不同物流中心的分配问题，也是用户最优选择问题，目标是使得所有客户的总费用达到最低，目标函数如下：

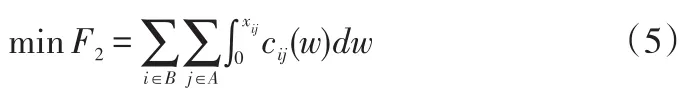
（2）约束条件。由于所有客户的需求量必须满足，可得到约束条件如下：

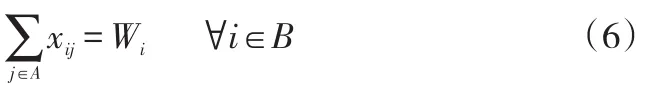
保证所有客户只在新建物流中心分配运输需求，没有建设的物流中心不分配运输需求，可得约束条件如下：

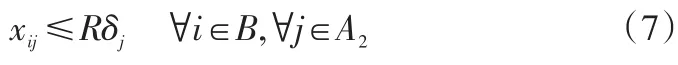
满足运输需求量有意义，即非负约束，可得：

4　求解算法

4.1最优解分析

上层规划是一个标准的0-1规划问题，求解算法较多，本文利用遗传算法进行求解。上层规划实际是一个客户需求分配问题，从式（7）可以看出，若δj=0，则xij=0，可以去掉；若δj=1，则xij≤R是肯定满足的，也可以去掉。故下层模型中只有一个等式约束，可以通过拉格朗日方法证明最优解的存在性。

引入拉格朗日函数，下层规划目标函数可以表示如下：

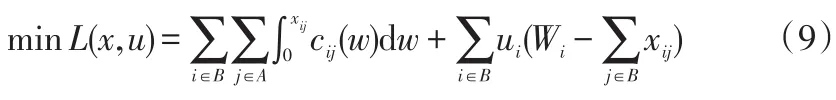
式（9）中ui表示下层规划式（6）约束的拉格朗日乘子。

利用拉格朗日方法中的K-T条件，求解上述问题的一阶条件，可得：

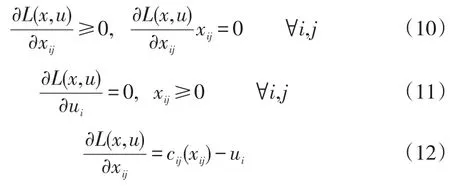
对式（10）和（11）进行化简可得一阶条件为：

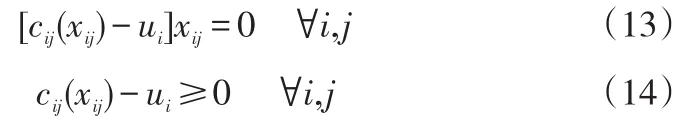
ui可以理解为客户i分配运输需求到各个物流中心的最小费用，且必须满足cij（xij）=ui。结果就是客户i到所有分配运输需求的物流中心费用是相等的，并且此费用小于或者等于没有分配运输需求的物流中心的费用。也就是说，客户所有选址费用都是最低且相等的，故下层规划满足用户最优的UE平衡，存在唯一最优解。

4.2Frank-wolfe算法设计

对于下层规划满足用户最优UE平衡的运输需求分配问题，最常用求解方法就是Frank-Wolfe算法，基本思想是：通过每次迭代将非线性规划问题转化为线性规划问题，即在某个可行解xi处用泰勒公式展开，利用一阶泰勒展开式逼近原来目标函数，最终转化为线性规划问题。

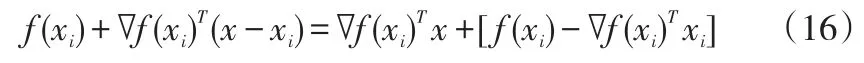
假设存在有限个最优解yi，下层规划运输需求分配的Frank-wolfe算法步骤如下：

Step1：初始化。选取初始可行点x0，允许误差ε＞0，置i=0。

Step2：根据目标函数min∇f（xi）Tx可知是求最小值，将初始点代入得到当前最优解yi。

(3) 方法3以及本文方法中桩间净距与抗滑桩截面宽度、高度都相关，呈线性增函数关系。其中，b-L曲线斜率相对于a-L曲线斜率小，表明桩间净距对抗滑桩截面宽度的变化更为敏感。

Step3：确定可行下降方向。若 ∇f（xi）T（yi-xi）≠0，则∇f（xi）T（yi-xi）＜0，故 可 行 下 降 方 向di=yi-xi，若则停止计算，输出xi，否则转到下一步。

Step4：进行一维搜索。从xi出发做一维搜索，寻找到最佳步长 αi，满足 minf［xi+α（yi-xi）］，其中 0≤α≤1，令xi+1=xi+αi（yi-xi），i=i+1，转到Step2。

4.3遗传算法设计

根据上层模型是一个标准的0-1规划问题，本文设计遗传算法对其求解。

（1）遗传操作设计。根据0-1整数规划模型特点，设计一种0-1编码。染色体的基因由数字0或1组成，种群大小一般选择30-100之间。本文上层所求的目标函数是求总费用最小，故可以直接采用目标函数作为适应度函数。遗传算法采用随机单点交叉策略，变异操作就是根据变异概率选取其中一条染色体，然后随机选取其中一个基因点位置进行变异，使其基因值“1”或“0”互换。

（2）复制操作方法。选择操作主要是将适应函数值较大的个体遗传到下一代，淘汰适应度值小的个体，本文主要采用轮盘赌和锦标赛相结合。首先，利用锦标赛规则，把每一次迭代过程中适应函数值最大的父代保留遗传到下一代。然后，利用轮盘赌原理，以随机概率的形式选择遗传下一代，概率是由个体适应度函数值与所有个体适应度函数值之比确定，选择遗传到下一代的概率pi由式（18）得到：

选择操作具体步骤如下：

Step1：计算所有个体的适应函数值，并排序，令i=1；

Step2：选出适应度函数值最大的个体，直接复制到下一代；

Step4：若i≥m-1，程序终止；否则转到下一步；

4.4算法步骤

根据本文设计的Frank-wolfe算法和遗传算法的结合，具体算法步骤如下，其中i表示迭代次数，Gen表示遗传算法最大迭代次数，Xi表示第i代种群。

Step1：种群初始化。随机生成m个初始种群Xi（新建物流中心选址结果），并置i=0。

Step2：将初始解Xi代入到下层模型，利用Frank-wolfe算法计算下层，获得当前最优解（客户在各个物流中心的需求分配）。

Step5：对种群Xi进行交叉操作，并淘汰不符合条件的染色体。

Step6：对种群Xi进行变异操作，并淘汰不符合条件的染色体。

Step7：产生新一代种群，Xi+1=Xi。

Step8：置i=i+1，转Step2。

5　算例分析

如图2所示，某大型公司需要在B区域新建至少一个物流中心，备选点主要有1，2和3三个地方，而此区域里原有一个物流中心4，所有物流中心需要满足6个客户的运输需求。

已知六个客户运输需求量依次为7 000kg、15 000kg、13 000kg、10 000kg、9 000kg和8 500kg。各个物流中心到所有客户之间的单位运输费率与距离见表1和表2，备选物流中心建设和运营费用见表3。

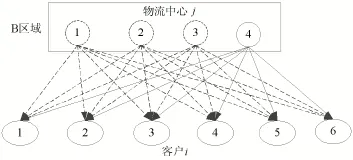
图2　考虑市场竞争的新建物流中心选址案例

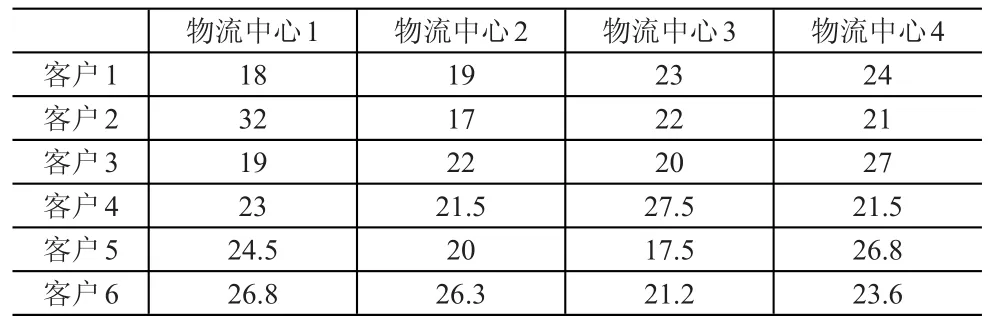
表1　物流中心到客户的单位运输费率（元·kg/km）

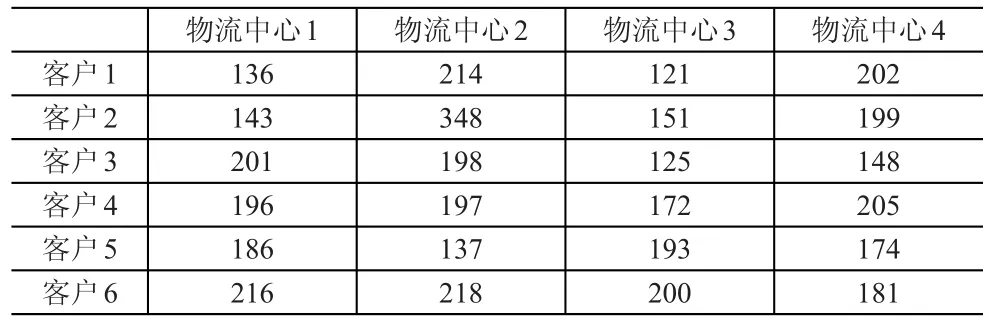
表2　物流中心到客户的运输距离（km）

表3　备选物流中心建设费用和运营费用（万元）

此外，本案例中Frank-wolfe算法中的参数ε=0.01，遗传算法中的种群大小为50，交叉概率为0.9，变异概率为0.05，最大迭代次数为500代，利用C++编程计算，在计算到435代左右趋于稳定，上层模型的总费用为13 477.587，得到的选址结果和用户运输需求分配结果见表4。

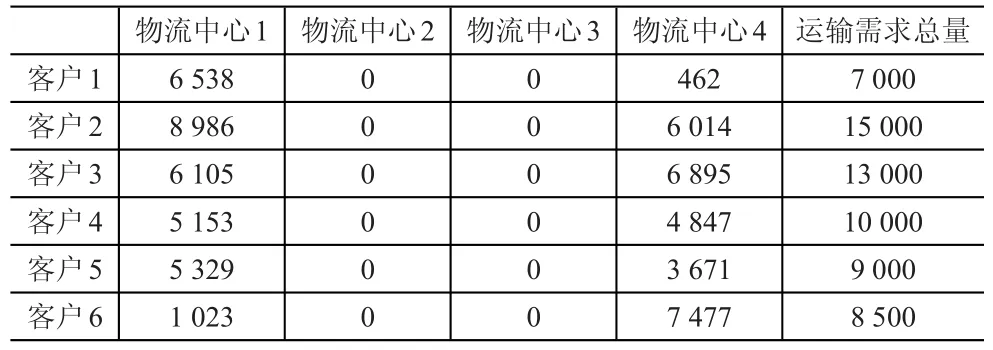
表4　新建物流中心选址结果与客户运输需求分配（kg）

从表4的结果中可以看出，新建物流中心的选址结果是在1处新建一个物流中心，同时由物流中心1和4共同承担所有客户的运输需求任务。

根据本案例设计的迭代次数为500，依次导出9个不同迭代次数得到的选址结果，见表5，表中“1”表示选择在此处新建物流中心，“0”表示不在此处新建物流中心。

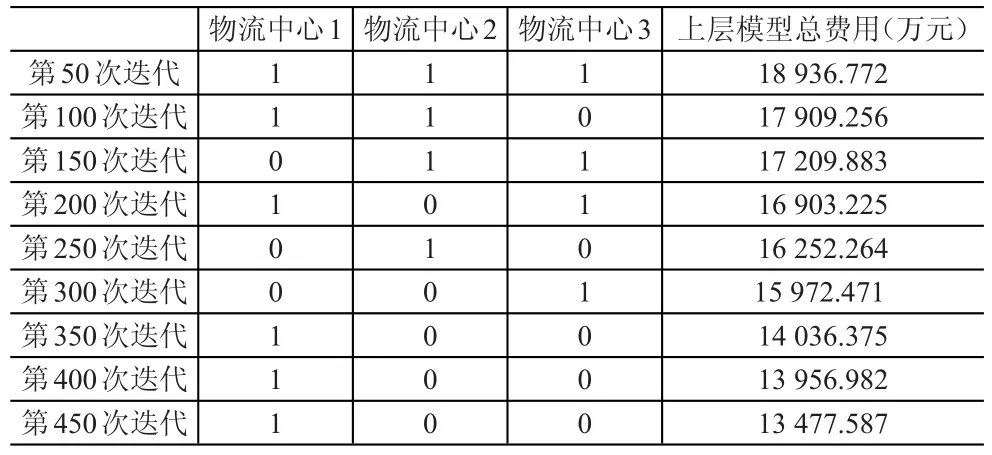
表5　不同迭代次数的选址结果

从表5可以得知，随着迭代次数的增加，上层模型的总费用随之减少，新建物流中心选址结果也在不断变化，从350代开始选址结果不再变化，但是上层模型的总费用还在不断减少，说明所有用户的运输分配还在变化，到450代时得到的结果和最终结果一致，且后50代迭代不再发生变化，说明算法已经收敛到最优解。

6　结论

本文考虑原有物流中心对新建物流中心产生市场竞争的条件下，对新建物流中心的选址和所有用户的运输需求分配进行研究，建立了基于市场竞争的新建物流中心选址的双层规划模型，设定新建物流中心的固定建设费用和运营费用为约束条件，设计了Frank-wolfe算法和遗传算法相结合的迭代算法对模型进行求解，并对双层规划模型的最优解进行讨论与证明。通过设计一个简单算例，验证了本文模型和算法的有效性，也为新建物流中心选址问题提供了一个新的思路与方法，具有较强的实践意义。但本文只考虑了两级配送模式，没有考虑多级配送，有待进一步研究。

［1］NozickL K.The fixedcharge facility location problemwithcoverage restriction［J］.TransportationResearch part E，2001，37，（4）：281-296.

［2］Klose A，Drexl A.Facility location models for distribution system design［J］. European Journal of Operational Research，2005，162（1）：4-29.

［3］王宝华，何世伟.不确定环境下物流中心选址鲁棒优化模型及算法［J］.交通运输系统工程与信息，2009，9（2）：69-74.

［4］Schuetz P，Stougie L，Tomasgard A.Stochasticfacility location with general long-run costs and convex short-run costs［J］.Computersamp;Operations Research，2008，35（9）：2 988-3 000.

［5］李振宇，杨松林.基于GIS的多级物流中心选址动态模型分析［J］.物流技术，2011，30（10）：81-83.

［6］李新运，唐保国，梁立魁.基于GIS和粒子群算法的两级物流配送中心选址优化方法及应用［J］.物流技术，2012，31（1）：78-82.

［7］高国飞，张星臣，徐彬，等.双层规划模型在供应链选址中的应用［J］.物流技术，2008，（8）：86-88.

［8］Bing Wang，Fu Xiao-kang，Chen Ting-gui.Modeling supply chain facility location problem and its solution using a genetic algorithm［J］.Journal of Software，2014，9（9）：99-103.

Study on Location Problem of Newly-built Logistics Centers with Market Competition Consideration

Li Lei1，Zheng Pengjie2
（1. Department of Management Engineering， Qinghai Communications Technical College， Xining 810003；2. Rail-line Administration Station， China Railway Siyuan Survey Design Group Co.， Ltd.， Wuhan 430063， China）

In this paper， we proposed the model and algorithm for the location allocation of a newly built logistics center under themarket competition circumstances， and then considering the competition from the original logistics center， established a duo-level locationallocation model， the aim of the upper level programming being to minimizing the total cost of the logistics center and that of the lower levelprogramming being optimal customer selection and minimal total expenses. Then according to the characteristics of the model， we designedan iterative algorithm that combined that Frank- Wolfe algorithm and the genetic algorithm for the solution of the model， and at the end，through a numerical analysis， demonstrated the validity of the model and algorithm.

logistics center； market competition； duo-level programming； genetic algorithm； Frank-Wolfe algorithm； location allocation

F252；F224

A

1005-152X（2016）01-0076-04

10.3969/j.issn.1005-152X.2016.01.020

2015-12-12

李蕾（1984-），女，青海西宁人，青海交通职业技术学院管理工程系讲师，硕士，研究方向：现代物流发展与运作模式；郑鹏杰（1989-），男，湖北武汉人，中铁第四勘察设计院集团有限公司线站处助理工程师，硕士，研究方向：现代物流园区规划与设计。