疲劳效应对蜂窝纸板系统的内共振条件参数影响的研究
范志庚, 卢立新, 王 军
(1.江南大学 包装工程系,江苏 无锡 214122;2.浙江科技学院 轻工学院,杭州 310023;3.中国包装总公司食品包装技术与安全重点实验室,江苏 无锡 214122)
疲劳效应对蜂窝纸板系统的内共振条件参数影响的研究
范志庚1,2, 卢立新1,3, 王军1,3
(1.江南大学 包装工程系,江苏 无锡214122;2.浙江科技学院 轻工学院,杭州310023;3.中国包装总公司食品包装技术与安全重点实验室,江苏 无锡214122)
研究了疲劳压缩条件下,蜂窝纸板内共振条件的参数变化规律。首先,对预压缩后的蜂窝纸板进行不同次数疲劳压缩,接着进行准静态压缩,最后将得到的应力-应变曲线多项式拟合后得到蜂窝纸板本构模型参数值。利用变分迭代法得到单自由度和二自由度蜂窝纸板内共振条件,最后由本构模型参数计算得到内共振条件参数的变化规律。该结果对避免蜂窝纸板缓冲包装设计内共振的产生具有一定意义。
蜂窝纸板;疲劳;本构模型;内共振
蜂窝纸板是目前使用较为广泛的一种环保缓冲材料。其具有承载强度高、成本低、缓冲性能好等特点, 已经是运输包装行业中代替木箱、发泡塑料的一种新型环保绿色包装材料。
20世纪90年代以来,很多研究人员对蜂窝纸板承载和能量吸收性能进行了深入实验和理论的研究。王志伟等[1-2]研究了蜂窝纸板平台应力理论模型和能量吸收理论模型。王志伟[3-4]研究了正切型非线性包装系统破损边界。姜久红等[5]研究了基于关键部件的三次和双曲正切型非线性包装系统破损边界。郭彦峰等[6]测试了蜂窝纸板冲击吸收特性和振动传递特性。然而,疲劳效应对蜂窝纸板力学性能的研究还较少。肖伟等[7]研究了疲劳振动条件下蜂窝纸板承载力和缓冲性能的变化规律。孙聚杰[8-9]研究了瓦楞纸板疲劳特性。王军[10]研究了双曲正切非线性包装系统的内共振条件。高德[11-13]研究了多种非线性系统的冲击响应和破损边界研究。范志庚等[14]研究了蜂窝纸板疲劳试样的内共振条件变化。疲劳效应对蜂窝纸板系统的内共振条件参数影响的研究还未见,本文将在疲劳实验的基础上,得到蜂窝纸板本构模型参数表,参考前期研究[14]得到的内共振条件,得到蜂窝纸板内共振条件参数的变化规律。
1材料与实验
为了研究蜂窝纸板的内共振条件,首先要进行蜂窝纸板预压缩实验和疲劳压缩实验,实验所用的材料和设备有:
1.1材料
本试验所采用蜂窝纸板尺寸为10 cm×10 cm, 厚度分别为 4 cm 厚的直立方体,芯纸定量为105 g/m2,厚度为0.19 mm,面纸定量为200 g/ m2,蜂窝纸板规格参数见表1

表1 蜂窝纸板样品规格参数
1.2主要仪器及设备
本实验采用的主要设备有:恒温恒湿试验机THS-A7C-100AS, 对实验材料进行预处理;万能电子材料试验机 LRX Plus,对材料进行准静态压缩;电液伺服材料试验系统,型号MTS322,对材料进行疲劳压缩实验。
1.3实验方法
1.3.1预处理
实验预处理环境条件为湿度50%,温度23℃,蜂窝纸板试样放入恒温恒湿箱内,预处理24小时以上。
1.3.2预压缩
在万能电子材料试验机上进行预应变率为15%的蜂窝纸板预压缩。
1.3.3疲劳压缩实验
蜂窝纸板预压缩后,在电液伺服材料试验系统上进行疲劳压缩实验,条件为疲劳压缩率10%,压缩频率10 Hz,压缩次数分别为10 000,20 000,30 000,50 000次的疲劳试验,每组实验为,实验数据取每组平均值。
1.3.4疲劳试样准静态压缩试验
参照GB/T 8168-2008 包装用缓冲材料准静态压缩试验方法进行准静态压缩试验,将疲劳试样放在万能电子材料试验机,取8个试样平均值,得到蜂窝纸板试样的疲劳后应力-应变曲线。如图1所示。


(a) t/l=0.0263(b) t/l=0.0238(c) t/l=0.0219图1 疲劳压缩后蜂窝纸板应力-应变曲线Fig.1Effectoffatiguestress-strainrelationshipofpre-compressedhoneycombpaperboard
1.4蜂窝纸板疲劳压缩后本构模型的选取
从图1可以看出,蜂窝纸板的应力-应变曲线可以用多项式拟合[15],本文通过实验,采用8阶多项式进行拟合,材料拟合曲线与实验值如图2所示,
(1)
蜂窝纸板本构模型参数是通过matlab软件拟合得到的,如表2~表4所示。从表2~表4可以看出本文采用8阶多项式完全可以满足研究需要。关键部件与产品之间的等效弹性刚度a1随着压缩次数的增加而减小。
2蜂窝纸板包装系统内共振条件
2.1单自由度蜂窝纸板包装系统内共振条件
单自由度蜂窝纸板包装系统的动力学模型由式(1)对时间取二阶导数来描述成式(2):
(2)

(3)

表2 蜂窝纸板本构模型拟合参数(t/l=0.026 3)

表3 蜂窝纸板本构模型拟合参数(t/l=0.023 8)
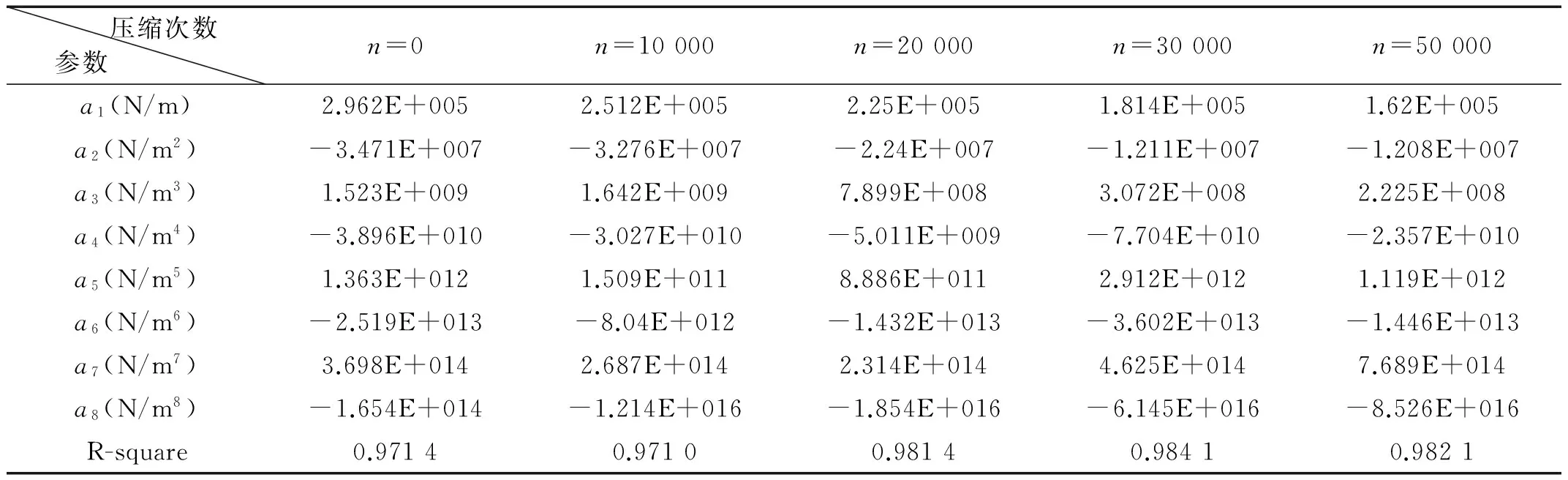
表4 蜂窝纸板本构模型拟合参数(t/l=0.021 9)
(4)

图2 本构模型参数拟合效果(t/l=0.026 3)Fig.2 Fitting effects of constitutive model parameters(t/l=0.026 3)
2.2二自由度蜂窝纸板包装系统内共振条件
二自由度蜂窝纸板包装系统动力学模型可以表示为
(5)
式中:m1代表关键零部件的质量,m2代表产品主体的质量,k1表示连接部刚度,ai表示蜂窝纸板本构模型参数,h为跌落高度。
(6)


Ω1=ω01
(7)
Ω2=ω01
(8)

(9)

(10)
ω01=ω02
(11)
3疲劳效应对蜂窝纸板包装系统内共振条件的影响
3.1疲劳效应对单自由度蜂窝纸板包装系统内共振条件的影响
从式(4)可以看出单自由度系统内共振与ω01有关,将通过实验得到的蜂窝纸板应力-应变曲线用matlab软件拟合后,得到蜂窝纸板本构模型参数数据代入式(4)计算得出对于单自由度蜂窝纸板包装系统ω01的值见表5。

表5 单自由度蜂窝纸板包装系统内共振参数
从表5可以看出,单自由度蜂窝纸板包装系统内共振条件参数ω01随着压缩次数的增加在30 000次之前呈现出一定在0.60附近的波动,超过30 000次后,出现明显下降,说明单自由度蜂窝纸板包装系统疲劳损伤后,在较低的等效频率比下将出现内共振。
3.2疲劳效应对二自由度蜂窝纸板包装系统内共振条件的影响
从式(7)~式(11)可以看出二自由度系统内共振与ω01和ω02有关,通过定义计算得出二自由度系统的ω01和ω02:
(12)
(13)
这里假设关键部件的质量m1=0.02 kg,产品主体的质量m2=0.48 kg,关键部件与产品之间的等效弹性刚度k1=19 600 N/m。
将通过实验得到的蜂窝纸板应力-应变曲线用matlab软件拟合后,得到蜂窝纸板本构模型参数数据代入式(12)和式(13),计算得出对于二自由度蜂窝纸板包装系统ω01和ω02的值见表6。

表6 二自由度蜂窝纸板包装系统内共振参数
从表6可以看出,二自由度蜂窝纸板包装系统内共振条件参数ω01随着压缩次数的增加逐渐增大,内共振条件参数ω02在一定范围内波动,从表2-表4中可以看出a1随着疲劳次数增加而减小,从式(12)看出,减小关键部件与产品之间的等效弹性刚度k1,从而可以减小ω01的值,说明二自由度蜂窝纸板包装系统疲劳损伤后,通过改变关键部件与产品之间的等效弹性刚度才能保护产品。
4结论
疲劳效应对蜂窝纸板包装系统内共振条件的变化影响较大。
对于单自由度蜂窝纸板包装系统,在材料疲劳初期,内共振条件变化不大,在一定范围内波动,而在疲劳后期,内共振频率逐渐变小,内共振条件与材料疲劳后本构关系有关,在较低的等效频率比下将出现内共振。
对于二自由度蜂窝纸板包装系统,内共振条件ω01随着疲劳程度的加剧而变大,内共振条件参数ω02在一定范围内波动,因此二自由度蜂窝纸板包装系统在疲劳损伤后,可以通过适当改变关键部件与产品之间的等效弹性刚度的方法保护产品。
[ 1 ] Wang Zhi-wei, E Yu-ping. Mathematical modeling of energy absorption property for paper honeycomb in various ambient humidities[J]. Materials and Design, 2010, 31 (9): 4321-4328.
[ 2 ] E Yu-ping. Energy absorption properties of paper-based packaging materials as response to various ambient humidities[J]. Applied Mechanics and Materials, 2012, 200:155-159.
[ 3 ] Wang Zhi-wei. On evaluation of product dropping damage [J]. Packaging Technology and Science, 2002, 15(3): 115-120.
[ 4 ] Wang Zhi-wei. Dropping damage boundary curves for cubic and tangent package cushioning systems [J]. Packaging Technology and Science, 2002, 15(5): 263-266.
[ 5 ] Jiang Jiu-hong, Wang Zhi-wei. Dropping damage boundary curves for cubic and hyperbolic tangent packaging systems based on key component[J]. Packaging Technology and Science, 2012, 25(7): 397-411.
[ 6 ] Guo Yan-feng, Zhang Jing-hui. Shock absorbing characteristics and vibration transmissibility of honeycomb paperboard[J]. Shock and Vibration, 2004, 11(5): 521-531.
[ 7 ] 肖伟,李大纲,徐朝阳.疲劳振动对蜂窝纸板承载力和缓冲性能的影响[J].包装工程,2009,30(1):14-17.
XIAO Wei, LI Da-gang, XU Zhao-yang. Influence of fatigue vibration on the load capacity and cushion performance of honeycomb cardboard[J]. Packaging Engineering, 2009, 30(1):14-17.
[ 8 ] 孙聚杰. 瓦楞纸板承载能力疲劳损伤曲线研究[J]. 包装工程, 2008, 29(12):4-10.
SUN Ju-jie. Research on fatigue damage curve of corrugated cardboard[J]. Packaging Engineering,2008, 29(12): 4-10.
[ 9 ] 孙聚杰, 卢立新. 剩余强度模型对瓦楞纸板疲劳振动的分析研究[J].包装工程, 2007, 28(8):19-21.
SUN Ju-jie, LU Li-xin. Study of fatigue vibration Effect on corrugated fiberboard based on residual strength model[J]. Packaging Engineering, 2007, 28(8): 19-21.
[10] Wang J, Khan Y, Lu L X, et al. Inner resonance of a coupled hyperbolic tangent nonlinear oscillator arising in a packaging system[J]. Applied Mathematics and Computation, 2012, 218(15): 7876-7879.
[11] 卢富德,高德. 考虑蜂窝纸板箱缓冲作用的产品包装系统跌落冲击研究[J]. 振动工程学报,2012,25(3): 335-341.
LU Fu-de, GAO De. Study on drop impact of packaging system considering the cushioning action of honeycomb paperboard box[J]. Journal of Vibration Engineering, 2012,25(3):335-341.
[12] 高德,卢富德.考虑转动的双曲正切与正切组合模型缓冲系统冲击响应研究[J]. 振动工程学报,2012,25(1):6-11.
GAO De, LU Fu-de. The shock response of hyperbolic tangent and tangent comprehensive model on cushion system considering rotary motion[J]. Journal of Vibration Engineering, 2012,25(1):6-11.
[13] 卢富德,高德,梁爱锋.立方非线性双层包装在矩形方波冲击下破损边界曲线的研究[J].包装工程,2008, 29(12):7-10.
LU Fu-de, GAO De, LIANG Ai-feng. Study of damage boundary curve of cubic non-linear double layer package under rectangular pulse[J].Packaging Engineering,2008,29(12):7-10.
[14] Fan Zhi-geng, Lu Li-xin. Effect of fatigue damage on inner-resonance conditions of pre-compressed honeycomb paperboard system[J].Advances in Mechanical Engineering, 2014(8):1-4.
[15] Jiang Jiu-hong, Wang Zhi-wei. The research on the vibration characteristics for honeycomb paperboard cushioning package system[J]. Journal of Hubei University of Technology, 2006, 21(3):18-20.
[16] He Ji-huan, Wu Xu-hong. Variational iteration method: new development and applications [J]. Computers and Mathematics with Applications, 2007, 54(7/8): 881-894.
Effects of fatigue damage on inner-resonance condition parameters of a honeycomb paperboard system
FAN Zhi-geng1,2, LU Li-xin1,3, WANG Jun1,3
(1. Department of Packaging Engineering, Jiangnan University, Wuxi 214122, China;2. School of Light Industry, Zhejiang University of Science and Technology, Hangzhou 310023, China;3. Key Laboratory of Food Packaging Techniques and Safety of China National Packaging Corporation, Wuxi 214122, China)
The variation of inner-resonance condition parameters of a honeycomb paperboard system was studied under fatigue compression. Firstly, the pre-compressed honeycomb paperboards were tested with different numbers of fatigue compression. Then, they were tested with quasi-static compression. The obtained stress-strain curves were fitted with polynomials to gain parameters of honeycomb paperboard’s constitutive model. The inner-resonance conditions of a single-DOF honeycomb paperboard system and a 2-DOF one were acquired with the variational iteration method. Finally, the varying laws of the two systems’ inner-resonance condition parameters were obtained through calculations of parameters of honeycomb paperboard’s constitutive model. The results were significant to avoid inner-resonances during honeycomb paperboard cushion packaging design.
honeycomb paperboard; fatigue; constitutive model; inner-resonance
10.13465/j.cnki.jvs.2016.11.032
2015-03-30修改稿收到日期:2015-05-08
范志庚 男,硕士,浙江科技学院讲师,博士研究生,1979年5月生
卢立新 男,博士,教授,博士生导师,1966年8月生王军 男,博士,副教授,1982年11月生
TB484.1;TB485.3
A

