在操作中感悟 在参与中建构

王娟

数学概念教学是学生掌握数学基础知识和基本技能的核心，正确理解数学概念是学好数学的基础。近年来，我对各年级的期中、期末考试卷进行分析时，发现有相当一部分学生的错误都落在概念上，特别是有些优等生在运用概念进行判断、填空时也出错，随着年级的升高，所学概念的增多，在概念处的错误比例也逐渐递增，可见学生对概念内涵的理解和把握不完善，灵活运用不够。并且在许多概念课的公开教学中，我发现老师在概念教学中孤立地讲授概念，过分注重概念的叙述，注重概念的应用，而不注重概念的形成过程。都存在着教学环节设计不够巧妙，方法不够灵活或者重难点突破不透，将概念强加给学生的现象，导致概念教学的实效性不强。

由此看来，在小学数学概念教学中，如何引导学生主动建构概念，突破概念教学的重难点，已成为我们每一位数学教师亟待解决的一个问题。本文就以《分数的意义》一课为例，谈谈自己的实践与思考。

一、复习旧知，引入概念

数学概念的引入，是学生能否学好概念的关键一步。引出新概念的过程，是揭示概念的发生和形成过程，而各个数学概念的发生形成过程又不尽相同，不同的概念引入的方法就不同。

在教学《分数的意义》时，采用复习旧知引入概念。

师：我们已经认识了分数，关于分数你已经知道了什么？

生：分数由分子、分母、分数线三部分组成。

师：分数线表示什么？

师（提示）：分数线表示平均分。

师：分子、分母分别表示什么？

生：分母表示平均分得份数，分子表示取其中的几份。

师：你能任意说一个分数，并说说这个分数表示的意义吗？

生1：表示把一个物体平均分成5份，表示其中的3份就是这个物体。

生2：表示把一个物体平均分成3份，表示其中的1份。

……

师：今天我们继续研究分数的意义。

通过复习切入新知，唤起学生原有的知识经验，找准学生的知识起点。

二、动手操作，建构概念

心理学家皮亚杰指出：“活动是认识的基础，智慧从动作开始。”书上的数学概念是平面的，现实却是丰富多彩的，照本宣科，简单学习自然无法让这些数学概念成为孩子们数学知识的坚固基石。如果我们能够让孩子们的多种感官参与学习，让平面的书本知识变得多维、立体，让学生的感觉和思维同步，相信能取得很好的教学效果。

教学《分数的意义》时，我主要通过两个参与式的教学活动来帮助学生建构分数的意义、单位“1”以及分数单位的概念。活动一是让学生准备了一米长的绳子、一个正方形、4个苹果、12个正方形。然后4人一小组活动，任选一种或几种学具表示出。活动二是继续拿出12个正方体分一分，看看有多少种不同的分法，分别用分数表示出来。通过学生的动手操作、合作交流、归纳概括，让学生体会到，以前学过的平均分的是一个物体，而今天扩展到由一个或多个物体组成的一个整体，自主地建构“单位1”的概念。这些概念的获得是通过活动建构起来的，而不是教师强加给学生的，充分体现了新课程倡导的在活动中建构的教学理念。使学生对分数的认识提高到了一个新的层次，同时也为以后学习分数应用题打下了坚实的基础。

三、变式练习，巩固概念

教学时，教师不仅要教会学生怎样来构建概念，更要让他们能用所掌握的概念去创造性地解决一些实际问题，提高学生对数学概念的运用技能。因此，应设计一些变式练习，帮助学生明确概念的外延，达到巩固概念的目的。

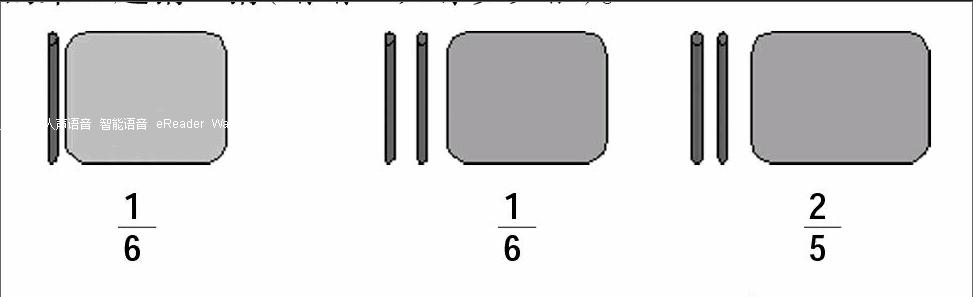
《分数的意义》这节课的重点是理解分数的意义，因此，在完成书本上相关习题的前提下，还应设计一些综合性的习题，如巩固练习的第3题猜一猜（猜猜一共有多少根）。

这道题设计得很好，知道1份是单位“1”的，是1根，求总数几根，就是求1份是1根，6份是几根的问题，当1份是单位“1”的，是2根时，求总数几根，就是求1份是2根，6份是几根的问题……这样的设计，不仅深化了学生对分数意义的理解，还有效地沟通了整数与分数的联系，同时使学生感受到同一个分数，“单位1”的量变化，所对应的数量也随之变化。并引导学生通过观察，感受到“单位1”的量的变化是如何影响分数所对应的数量的变化的。这样的设计，提升了概念的应用价值，培养了学生的思维能力。

总之，概念的引入、形成、巩固和运用，是学习和掌握任何一个数学概念必须具备的过程。教师在概念教学中，要结合概念的特点和学生的实际，灵活设计不同的环节，采取多种教学策略，使学生在掌握数学概念的同时，提高数学能力。

编辑 王团兰