例析函数含参问题中的分类讨论与分段讨论

魏国达

（福建省清流县第一中学）

例析函数含参问题中的分类讨论与分段讨论

魏国达

（福建省清流县第一中学）

在高中数学思想方法中，分类与整合思想是非常重要的思想方法之一。这种思想在解决有关含参的问题中更是显出它的重要性。分类与整合思想有两种形式：参数的分类讨论与自变量的分段讨论。学生在运用时往往混淆不清，特别是在整合的结果上分不清是取交还是取并。通过对例题的解析谈谈分类讨论与分段讨论。

数学思想；分类讨论；分段讨论

高中数学的七大数学思想中，分类与整合思想是很重要的思想方法之一。福建2015年《考试说明》中指出：“分类与整合思想不仅是解决数学问题的常用方法，也是其他自然科学和社会科学研究的基本逻辑方法，高考把分类与整合思想放在比较重要的位置，并以解答题为主进行考查。”分类与整合思想方法应用于高中数学的各个章节中，特别是在分段函数与含有参数的函数问题中更是体现得淋漓尽致。在含有参数的函数问题中讨论有两类：对于参数的分类讨论和对于自变量的分段讨论，然而学生在对于是分类讨论还是分段讨论混淆不清,也不知如何整合结果。这里结合一些例题谈谈函数中含参问题的分类讨论与分段讨论。

一、对参数的分类讨论

1.含参的函数问题中研究的对象是自变量时，若需对参数进行分类讨论，且自变量的范围在参数的每一种分类中都是完整的，这种讨论方法为参数的分类讨论法，其整合的结果为各类结果的并集。

解：（fx）的定义域为R

由f′（x）=x2-（a+2）x+2a=（x-a）（x-2）=0得x=a或x=2

（1）当a＜2时，由f′（x）＞0得x＜a或x＞2，由f′（x）＜0得a＜x＜2，则（fx）的增区间为（-∞，a），（2，+∞）；减区间为（a，2）；

（2）当a=2时，f′（x）=（x-2）2≥0恒成立，（fx）的增区间为R，无减区间；

（3）当a＞2时，由f′（x）＞0得x＜2或x＞a，由f′（x）＜0得2＜x＜a，则（fx）的增区间为（-∞，2），（a，+∞）；减区间为（2，a）；

综上：当a＜2时，（fx）的增区间为（-∞，a），（2，+∞）；减区间为（a，2）；当a=2时，（fx）的增区间为R，无减区间；当a＞2时，（fx）的增区间为（-∞，2），（a，+∞）；减区间为（2，a）；

注：本题研究的对象是自变量x，通过比较f′（x）的两个值a 与2的大小，对a进行分类讨论。在a的每一种情形中，都是在自变量x的范围R上研究，则结果为各类结果的并集。

2.含参的函数问题中研究的对象是参数时，常用分离参数的方法。若参数不好分离，则对参数进行分类讨论，且在每一类的讨论中自变量的范围保持完整不变。其参数所求的结论是各类结论的并集。

解：（fx）的定义域为（0，+∞）

（1）当a=0时，（fx）=x（x＞0）在（1，2）上为增函数，符合题意；

（3）当a＜0时，由（fx）＞0得x＜3a或x＞-a，（fx）的增区间为（-∞，3a），（-a，+∞），由题意得区间（1，2）是（-a，+∞）的一个子集，

注：本题研究的对象是参数a，由f′（x）≥0不好分离参数，则根据f′（x）=0的两根-a与3a的大小关系分类，求出增区间，利用（1，2）是f（x）的增区间的一个子集解决问题。在a的每一种情形中，x的范围（1，2）没有变化，因而这是一个分类讨论问题，参数a的取值范围是三种情形结果的并集。当然此题也可由f′（x）≥0在（1，2）恒成立，用二次函数的图象解决。

二、对自变量的分段讨论

用分离参数的方法研究含参问题中参数的取值范围时，若在分离参数的过程中要对参数的系数进行讨论，即要把自变量的范围分割成几个小范围进行求解时，则应对自变量采取分段讨论的方式，其参数的结果应取每段结果的交集。

综上：a的取值范围为［-2，2］。

注：本题中分离参数时由于参数的系数x的符号无法确定，因而要对x的范围进行分割处理，所以本题要对x进行分段讨论。其参数的范围是各段参数范围的交集。

（1）当x=0时，0≤0恒成立，则a∈R；

三、分类讨论与分段讨论的区别与联系

含参的函数问题中，不论研究对象是参数还是自变量，若以研究对象作为主体进行讨论时，则是分类讨论，其结论为各类结论的并集；若研究对象不动，以另一个对象为主体进行讨论时，则是分段讨论，其结论为各段结论的并集。以研究对象作为主体进行讨论其实是对研究对象自己进行分段讨论；研究对象不动，以另一个对象为主体进行讨论时，其实是对另一对象进行分类讨论。这两种分类方法实际上是解决问题的两种不同的思维途径，它们之间是可以相互转化的，如解决含参问题中求参数的范围时，既可对参数分类讨论，也可对自变量进行分段讨论。

（1）当Δ=a2-4≤0时满足条件，解得：-2≤a≤2；

综上：a的取值范围为［-2，2］。

注：此种方法结合二次函数的图象与x轴的交点个数和对称轴的位置进行分类，实际是在对参数a进行分类讨论，其结果取各类结果的并集。但这种方法很容易由于考虑不周全而漏解。

例4.另解：由于f′（x）=cosx-a

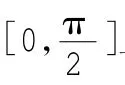
总之，含参问题中都是围绕着所求对象展开的，无论是对哪个量进行讨论，分类的对象都要科学分类，且分类标准要统一，做到不重不漏，并能科学地研究、合理地整合结果。

·编辑 鲁翠红