中考试题掠影

周宏伟

整式乘法与因式分解是学习代数的基础，主要突出对字母的运算技能，尤其是两个乘法公式的正向与逆向运用. 一般情况下，中考试题对其要求注重基础，强调能力，试题多以填空和选择为主，由于这部分内容主要涉及运算能力，所以往往渗透在数学的其他知识之中，是整个数学大厦的基石.

考点1 考查对乘法公式的运用能力

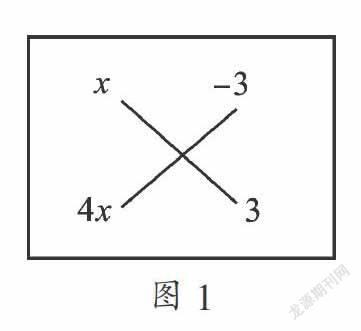
【试题评析】本题主要考查了分组分解法分解因式，正确分组是解题的关键. 但部分同学不能观察出分组特征，而是先把原多项式展开，然后重新进行组合，得到原式=x2+3x2-9x-9=4x2-9x-9，此时，似乎无法下手. 事实上，我们可以运用“十字相乘法”对其进行分解，即把首项4x2拆成x·4x，末项（-9）拆成（-3）×3，然后交叉相乘，并把相乘的结果相加，其结果等于中间项-9x（如图1），

考点4 考查对图形的理解能力

例4 （2014·宁波）一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是______（用含a、b的代数式表示）.

【思路分析】本题着重考查同学们对图形的观察、理解能力，如何运用图形给出的信息是解题的关键，计算图②中阴影部分的面积可以考虑用大正方形的面积减去4个小正方形的面积进行求解，故求出大小正方形的边长成为解题的关键.

【试题解答】设大正方形的边长为x，小正方形的边长为y，由图①和图②可列出方程组得：

【试题评析】此题考查自然数的变化规律，归纳其规律需要分别从被减数、减数、差三个方面进行探寻，体现了从特殊到一般的思想方法.

（作者单位：江苏省东台市新街镇中学）