“分数除法”算理简析

浙江杭州市闻涛小学（310052） 王 乐

“分数除法”包括两部分知识，即“一个数除以整数”和“一个数除以分数”，它的计算方法是“除以一个不为0的数，就相当于乘以这个数的倒数”。算法很简单，学生也容易掌握，但很多学生对“为什么要这样算”弄不清楚。下面，我从两方面简要分析“分数除法”的算理。

一、简析“一个数除以整数”的算理

“一个数除以整数”的算理还是比较容易理解的。以“把一张纸的平均分成2份，每份是这张纸的几分之几”为例，求每份是多少，也就是求的是多少，学生理解起来比较容易。所以，课堂上，学生很容易总结出“除以一个不为0的整数，就相当于乘以这个整数的倒数”。但是，如果教学仅仅到此为止，我觉得是不够的，还应该引导学生从“份数”的角度来理解。如“将平均分成2份，求每份是多少”，换句话说，也就是已经知道了2份是，求1份是多少，即“一个数除以整数”就是知道了多份求一份的问题。如下图：

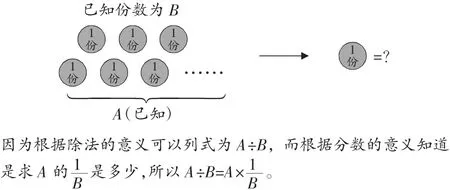
二、简析“一个数除以分数”的算理

一个数除以分数的算理不好理解，即使是我们成年人大部分也只是记住了算法，而算理早就忘得一干二净了。如教材中的例题：“小明小时走了2km，小红小时走了m。谁走的快些？”根据“路程÷时间＝速度”的数量关系，很容易列出算式，但是在理解算理上学生出现了困难。在学生经过讨论之后，我们发现学生也是可以用旧知解决新知的，即“为什么”。学生的方法大致如下：

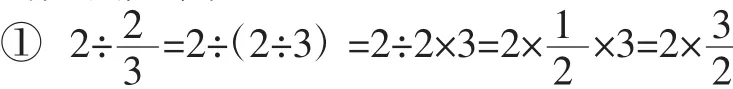
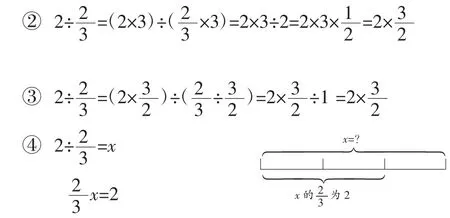
乍一看，这四种方法都可以证明这个算法是正确的，尤其是第四种方法，竟然跟书上的方法不谋而合，但当我们仔细分析这四种方法时，就会发现第四种方法的不同之处。前三种方法都是根据以前的算法进行推导，只是从算法的角度证明结论而已，而第四种方法虽然也是证明结论，但它是从分数的本质意义（把单位“1”平均分成几份，表示这样的一份或几份）入手理解算理的，这才是算法的本质。

仔细分析不难发现，“一个数除以分数”的过程，实际上是知道部分求整体的过程，如何由部分求出整体是算理的本质。如下图：

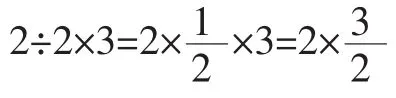
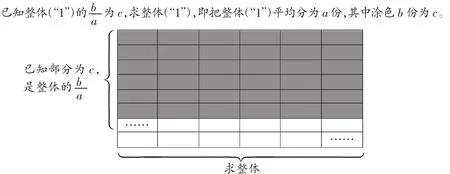
根据“总量÷数量＝单位量”的数量关系，很容易列算式为c÷。算理思考过程如下：

实际上，“除以整数”和“除以分数”都是求单位量（即1份数），只是角度不同，前者是已知多份数求1份数，后者是已知1份数的部分求1份数。

总之，教师在教学过程中要关注数学的本质，这样才能从根本上引导学生理解所学知识，使他们形成良好的认知结构。