基于遗传算法的锥齿轮优化设计
张 慧 李吉祥 徐 博
(太原重型机械集团有限公司)
锥齿轮传动转速范围较大、承载能力较强,因此被广泛应用于各种机械传动设备。对锥齿轮进行优化设计,减小其质量和体积,延长使用寿命在其设计过程中非常重要。但是按照锥齿轮设计的标准系列方法不能够很好地解决目前的问题。由于锥齿轮传动的优化设计是混合了离散变量的非线性优化问题,遗传算法(简称GA)借鉴生物进化过程自然选择与遗传机制,使问题的解不断改进的一种智能搜索算法,具有广泛的适应性,尤其适合处理复杂参数和非线性优化问题。因此,遗传算可以应用于锥齿轮传动优化设计中。
一、锥齿轮优化设计模型的建立
1.建立目标函数
由于锥齿轮的体积大小直接影响到加工和装配,为了使结构更加紧凑,减小齿轮重量,节约生产材料和成本,因此选用锥齿轮体积之和作为设计的目标函数
式中:da1——小锥齿轮齿顶圆直径;
da1——大锥齿轮齿顶圆直径;
βm——齿宽中心螺旋角;
R——锥齿轮外锥距;
ΨR——齿宽系数;
Rm——锥齿轮的平均锥距。
2.确定设计变量
锥齿轮传动的独立变化参数有小锥齿轮齿数Z,大端模数m,齿宽系数ΨR,中点螺旋角βm。故取设计变量为:x=(βm,Z1,m,ΨR)T=(x1,x2,x3,x4)T
3.建立约束条件
(1)齿面接触强度约束
计算接触应力σH与许用接触应力[σH]之间的关系:

(2)齿根弯曲强度约束
齿轮的计算弯曲应力σF与许用弯曲应力[σF]之间的关系

m——锥齿轮的模数;u——齿数比;
K——齿轮安全系数;YFS——锥齿轮齿形系数;
(3)设计变量的边界条件
①齿轮中点螺旋角的上、下限约束条件
15°≤βm≤40°
②小锥齿轮的齿数约束条件
13≤Z1≤Z1max
③齿轮模数约束条件
2≤m≤8
④齿宽系数约束条件
0.25≤ΨR≤0.3
由以上可得锥齿传动的数学优化模型为:

(4)适应度函数的构造
外点惩罚函数法是常用的一种惩罚函数方法,其基本的原理是将约束优化问题转化成为等价参数目标函数,即式子中:用G[gm(x)]=来定义全域,当迭代点在可行域内时,有gm(x)≥0惩罚函数不受惩罚,否则gm(x)<0,惩罚函数受惩罚。为在优化的过程中随着迭代次数K 的增大而在不断变化的参数,即惩罚因子。可见,外点惩罚函数就是将惩罚函数在可行域的外部逐渐逼近要求约束问题的最优化解的过程,按照该方法构造适应度函数。
v(x)=f(x)+p(x)
式中:x——染色体;
f(x)——目标函数;
p(x)——惩罚项。
本文锥齿轮优化目标为体积和最小,相应的适应度函数为:
当x 可行时p(x)=0
当x 不可行时p(x)=-r1[g(x)]2-r2[g2(x)]2<0
取锥齿轮齿面的接触惩罚因子r1=1,弯曲条件的惩罚因子r2=0.5
二、程序与仿真结果
1.锥齿轮遗传优化算法框图
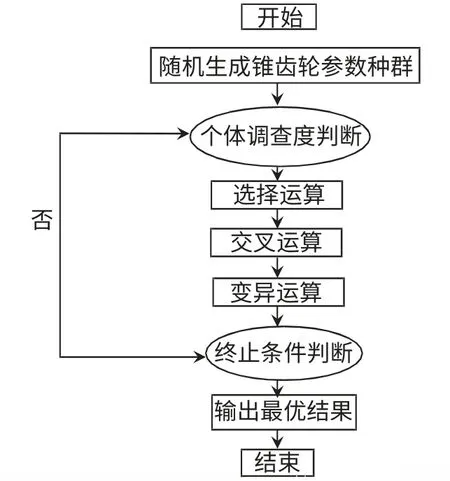
图1 锥齿轮遗传算法程序框图Fig.1 Bevel gear genetic algorithm block diagram.
2.优化设计适应度M-文件
定义适应度函数M-文件
function[sol,y]=GA_mp(sol,options)
%设计变量;中点螺旋角x(1);小锥齿轮齿数z=x(2);大端模数m=x(3);齿宽系数x(4)。
x(1)=sol(1);x(2)=sol(2);x(3)=sol(3);x(4)=sol(4);
%目标函数
u=3;%齿数比
ha=1;%齿高系数
d1=x(2)*x(3)/2;%小锥齿轮分度圆直径
d2=u*d1;%大锥齿轮分度圆直径
R=d1*sqrt(1+u^2);%外锥距
Rm=R*(1-0.5*x(4));%平均锥距
da1=(x(2)+2*ha)*x(3);%小锥齿轮齿顶圆直径
da2=(x(1)*u+2*ha)*x(3);%大锥齿轮齿顶圆直径
f=pi/4*x(4)*R*(Rm/R)^2*(da1+da2)^2/cos(x(1)*pi/360);%目标函数体积
%以某种型号锥齿轮减速器为例,设置初始种群
bounds=[15 45;13 17;2 10;0.25 0.3];
initPop=initializega(50,bounds,'A_mp',[]);
K=1.5;T1=45.1;u=3;
3.优化计算结果
****锥齿轮传动遗传算法最优解*****
中点螺旋角: β=18.7282
小齿轮齿数:z1=18.7282
齿轮的模数:m=2.0000 mm
齿宽系数: ψ=0.2500
锥齿轮体积:V=164768.5135 mm^3
经过运算确定小齿轮的齿数:z1=19
模数:m=2
齿形系数:ψ=0.25
****凑整解性能约束值****
齿面接触强度约束函数值
g1y=595.7808 Mpa
齿根弯曲强度约束函数值
g2y=248.7019 Mpa
此时在满足承载能力的条件下,最小体积为V=164768.5135 mm^3,充分节省材料成本。
4.适应度函数线图

图2 锥齿轮遗传算法优化过程图Fig.2 Bevel Gear genetic algorithm optimization process diagram.
本文建立了锥齿轮传动过程中多维非线性约束的数学优化模型,通过惩罚函数构造适应度函数,利用Matlab 中的遗传算法工具箱编程计算得到了锥齿轮传动的体积和最优解,同时绘制出遗传过程中个代适应度平均值线图,更直观地描绘出遗传算法的搜索过程,从而为锥齿轮传动减速器的设计过程中节约金属材料,缩短研发周期,降低生产成本提供了理论参考和借鉴。
[1]郭仁生.机械工程设计分析和Matlab 应用[M].机械工业出版社,2012-03:97-305.
[2]罗潘,梁尚明,蒋立茂,等.基于多目标遗传算法的弧齿锥齿轮多学科优化设计[J].机械设计与制造,2012(08):6-8.
[3]梁华琪.弧齿锥齿轮传动的多目标优化设计[J].现代机械,2005(01):18-19.
[4]刘光磊,樊红卫,谷霁红.一种弧齿锥齿轮传动性能优化方法[J].航空学报,2010,31(08):1680-1687.
[5]杜海霞.基于遗传算法的锥齿轮减速器优化设计[J].机械制造与研究,2011,40(01):28-29.
[6]李文涛.弧齿锥齿轮优化设计的数学模型[J].机械管理开发,2009,24(01):7-8.
[7]杜海霞.锥齿轮减速器的遗传算法优化设计[J].现代制造技术与装备,2010(04):22-23.

