2014年4月2日智利海啸数值模拟与分析

赵联大，徐志国，王培涛，范婷婷，候京明

（1.国家海洋环境预报中心，北京100081；2.国家海洋局海洋灾害预报技术研究重点实验室，北京100081）

1 引言

海啸是由地震、火山喷发等因素引起的海水大规模波动形成的一种大洋长波。在深海大洋中，海啸波能够以时速500—1000 km 的速度传播。当海啸波移近岸边浅水区时，波速会减慢，波高陡增，可形成十数米或更高的水墙，极具破坏力，可造成严重伤亡[1]。

由历史统计来看，全球的海啸事件主要发生在板块边缘的地震火山带附近如太平洋地震带、地中海-喜马拉雅地震带等，其中环太平洋地震带是全球地震海啸事件发生最多的地区[2]。

南美洲太平洋东岸是东南太平洋的纳斯卡板块与南美板块的交界地带，是环太平洋地震带其中一段。纳斯卡板块以南部每年80 mm/a、北部每年65 mm/a 的速度俯冲到南美板块下[3]。板块作用造就了南美近海的秘鲁-智利海沟和南美陆地上的安第斯山脉。这一典型的海底俯冲带构造极易引发地震海啸。国土沿着海岸呈南北方向的狭长分布的智利即处于这一俯冲带上。历史上，智利近海和陆地区域地震多发，其中部分发生于海域的地震引发了海啸。1960年5月22日，智利沿海发生了9.5级地震，这是人类有仪器记录以来震级最大的地震。这次地震引发了25 m高的海啸，海啸不仅袭击了南美沿海，还传播到了整个太平洋。2010年2月27日，智利发生了8.8级地震也引发了巨大的海啸，海啸传到我国，我国东部沿海多个海洋站监测到海啸波，沈家门站监测到28 cm的最大海啸波幅[4]。

2014年4月2日07时46分（北京时），南美洲智利北部近海发生8.2 级地震[3]，震源深度25 km。地震引发了海啸波，在地震发生后的几个小时内，海啸波先后到达了智利、秘鲁、厄瓜多尔沿海，当地多个海洋站监测到了明显的海啸波[5]。

本文利用国家海洋环境预报中心的CTSU海啸数值模型对这次海啸事件进行了数值模拟，并根据模拟结果进行了对比分析。

2 海啸数值模型

毗邻南美洲的东南太平洋绝大部分海域水深数千米，只是在南美沿岸100 km 以里，水深才迅速变浅。海啸波在深水大洋区是线性浅水长波，因此本文采用线性海啸数值模型来模拟本次海啸。另外，由于无法获南美近海高精度的水深地形数据，本文无法采用高精度的嵌套网格模拟近岸的海啸，而是采用格林公式[6]对近岸的海啸波计算结果进行修正。

2.1 海啸源模型

由于观测数据的缺失，地震发生时初始海啸源（即海水体的变化情况）无法获得，所以本文采用业界常用的Okada海啸源模型（见图1）[5]，利用所获得的地震参数计算海啸初始场。其中，L为断层长度、W 为断层宽度、θ为断层走向角、δ为断层倾斜角、λ为断层滑动角。由于地震断层发生错动是个很短暂的过程，因此该海啸源模型假设海底面的升降变化能够立即引起海床上面的海水水体变化，海床的垂直升降幅度即为海水表面的初始水位。

2.2 海啸传播数值模式

国内外成熟的海啸数值模式有多种，如国家海洋环境预报中心开发的CTSU[7]、日本气象厅使用的TUNAMI[8]、美 国Cornell 大 学 开 发 的COMCOT[9]。几种模式各自具有不同特点，但基本都是对浅水方程进行求解。本文采用国家海洋环境预报中心开发的CTSU海啸数值模型。

CTSU 模式基于浅水方程，分别建立了球面坐标和直角坐标控制方程。CTSU模式的控制方程组为：

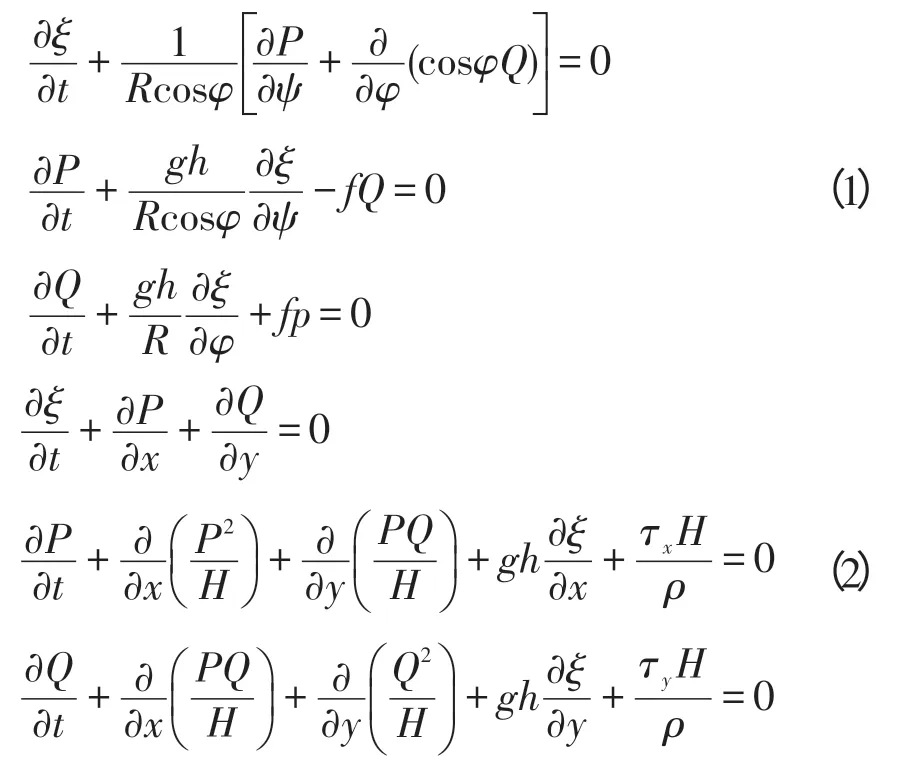
方程组（1）为球面坐标方程组，方程组（2）为直角坐标方程组。式中，ζ为水面高度；h为静止水深；H 为总水深；g 为重力加速度；ρ为水的密度；R 为地球半径；f为科氏力；τx,τy分别为x、y方向上的摩擦力；P、Q为x、y方向上的体积通量；φ和ψ分别为经度、纬度。

CTSU 采用半隐式有限差分格式求解控制方程，采用Arakawa C 网格，差分格式为蛙跳格式（leap-frog）。该模式具有计算速度快，支持并行计算等优点。

3 海啸数值模拟

2014年4月2日07时46分（北京时），南美洲智利北部近海（19.610°S，70.776°W）发生8.2级地震[2]，震源深度25 km。地震引发了海啸波，在地震发生后的几个小时内，海啸波先后到达了智利、秘鲁、厄瓜多尔沿海，当地多个海洋站监测到了明显的海啸波[5]。

3.1 震源参数选取

本文模拟所使用的海啸初始水位是由Okada海啸源模型计算得来（见图1 和图2）。而Okada 模型的计算则需要断层长度（L）、断层宽度（W）、断层走向角（θ）、断层倾斜角（δ）、断层滑动角（λ）、断层滑动量（d）、震源深度（D）等参数（见图1）。本模拟中断层走向角（θ）、断层倾斜角（δ）、断层滑动角（λ）、震源深度（D）等参数取自美国地质调查局（USGS）的震源机制解[10]，断层长度（L）、断层宽度（W）、断层滑动量（d）则是利用经验公式计算得出（见表1）。

由海啸源模型计算得知，初始水位最大抬升为2.94 m，最大下沉为-1.41 m（见图2）。

3.2 海啸计算

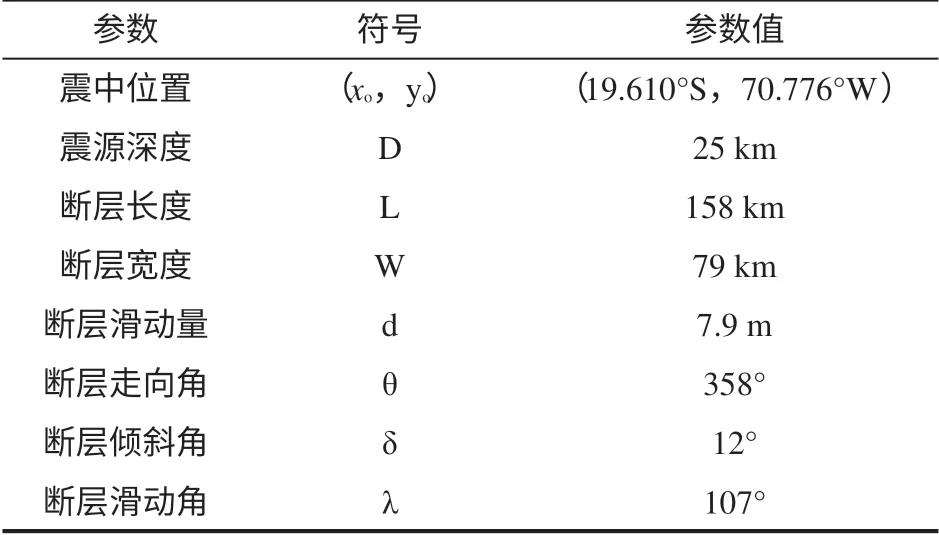
表1 本文海啸模拟所需震源参数表

本文模拟采用美国国家海洋大气局地球物理数据中心（NOAA/NGDC）的ETOPO1 水深和陆地高程数据[11]。计算区域范围为45°S—5°N，115°—65°W（见图3）。空间网格分辨率设置为2分。

地震海啸发生后，海啸波向四周传播（见图4）。在地震发生20 min 后海啸波到达了距离震中最近的智利北部沿岸，Iqui 和Pisa 海洋站监测到显著的海啸波；在震后0.5—1 h时间内，海啸波到达了秘鲁南部和智利中部；在1—3 h 内，海啸波到达了智利南部、秘鲁与厄瓜多尔。

震源附近的智利、秘鲁沿岸海啸波较大。智利沿岸的Iqui 和Pisa 海洋站的海啸波达到了1.5 m 左右，而震源以南的智利中南部海域、震源以北的秘鲁海域的海啸波相对较小，秘鲁沿岸的Mata站最大海啸波为0.39m，智利中南部的Anto、Cald、Papo、Coqu、Vald、Corr等站的最大海啸波在0.1—0.3 m左右。

由多个沿海站点的观测和模拟曲线对比图来看，CTSU 数值模式模拟的海啸波与实测曲线基本吻合，尤其是第一个海啸波，各站点的吻合程度都很好（见图5和表2）。

4 分析与讨论

4.1 海啸影响

本次智利海啸，其地震断层基本沿着南北走向，海啸能量的分布则垂直于断层走向而呈东西向分布和传播。位于海啸源东部的智利沿岸受海啸影响最大，距离海啸源最近的Iqui 和Pisa 的最大海啸波幅为1.5 m左右。这种级别的海啸波能够淹没海岸部分岸段，会造成一定的人员和经济损失。

此次海啸使智利沿海4000 多千米的海岸线上的90余万人进行了应急疏散，在距离震中最近的智利城市Iquique 和Arica，疏散持续了10 h[12-13]。而根据媒体报道，这次海啸至少造成6人死亡[12]。

随着传播距离的增大，海啸波能量逐渐耗减，波幅也逐渐变小，距离震源较远的智利中南部和秘鲁沿海的海啸实测数据证明了这一点。

4.2 模拟误差

CTSU数值模式模拟的海啸波与实测曲线基本吻合，尤其是第一个海啸波，各站点的吻合程度都比较好。

根据第一个海啸波的实测与模拟对比来看，海啸波幅差别较小，基本一致。但模拟的海啸波到达时间普遍比实测值要稍小。这主要是由于海啸源模型采用了经典的Okada 海啸源模型，这一模型是基于简单的逆断层错动原理，比较理想化。这就造成了初始海啸波以相对完美的水波向四周传播。而实际的地震海啸发生过程远比Okada模型复杂的多。通常海底断层破裂并非瞬时完成，而是存在一个时间过程。海底断层破裂在空间上也不均匀和对称，某些位置破裂程度相对较大，而有些位置则相对较小。海底破裂的差异造成海面的初始水位波形也与Okada海啸源模型产生差异。这就造成了事实上的海啸波与模拟的海啸波在时间传播上出现了时间差。

表2 智利与秘鲁沿海站点的第一波海啸波观测值与模拟值对比

对于有些站点，先导波之后的其余海啸波吻合程度则不是很好，有的实测波幅大于先导波。这主要是由于海啸波抵达这些站点时，因局地地形条件而形成反射、折射、震荡等过程，造成了波形的不规则变化。而本文的模拟采用的是空间分辨率为2分的水深和高程数据，这种分辨率对于模拟海啸波的传播过程是适合的，但模拟近岸浅水区的动力过程则显然不够。本文在近岸站点使用格林公式进行修正，但这也只是近似，而不够准确。所以海啸波在近岸浅水区的演变过程刻画得不够准确。沿岸站点除第一个海啸波外的其余海啸波实测与模拟曲线吻合程度不是很好。

5 结论

2014年4月2日（北京时间）智利北部近海发生了8.2 级地震并引发了大海啸，海啸对智利当地造成一定程度的伤亡和影响。本文利用CTSU海啸数值模式对这一海啸进行了数值模拟。模拟结果显示距离震源最近的智利北部受灾严重，沿海海洋站最大海啸波幅在1.5 m 左右。随着海啸波的扩散，秘鲁以及智利南部等海域也测到了明显的海啸波，但没有造成灾害性影响。对于第一个海啸波，本文的数值模拟结果与实测结果吻合较好，但由于理想化的数值模型与实际海啸产生过程存在差异，以及近岸水深地形数据的粗疏，后续海啸波的模拟结果与实际观测值存在一定的误差。

[1]UNESCO/IOC,International Oceanographic Commission Technical Series 85[K].Tsunami Glossary 2008,8.

[2]侯京明,李涛,范婷婷,等.全球海啸灾害事件统计及预警系统简述[J].海洋预报,2013,30(4):87-92.

[3]USGS, http://comcat.cr.usgs.gov/earthquakes/eventpage/usc000nzvd#summary

[4]于福江,王培涛,赵联大,等.2010年智利地震海啸数值模拟及其对我国沿海的影响分析[J]. 地球物理学报, 2011, 54(4): 918-925.

[5]Okada Y. Surface deformation due to shear and tensile faults in a half-space[J]. Bulletin of Seismological Society of America, 2008,75(4):1135-1154.

[6]Wang D L, Becker N C, Walsh D, et al. Real-time forecasting of the April 11, 2012 Sumatra tsunami[J]. Geophysical Research Letters,39,L19601,doi:10.1029/2012GL053081.

[7]于福江,叶琳,王喜年.1994年发生在台湾海峡的一次地震海啸的数值模拟[J].海洋学报,2001,23(6):32-39.

[8]IUGG/IOC Time project, numerical method of tsunami simulation with the leap-frog scheme[K].1997.

[9]CornellUniversity,http://ceeserver.cee.cornell.edu/pll-group/comcot.htm

[10]USGS,http://comcat.cr.usgs.gov/earthquakes/eventpage/usc000 nzvd #scientific_moment-tensor

[11]NOAA/NGDC,http://www.ngdc.noaa.gov/mgg/global/global.html

[12]Reuters,http://www.reuters.com/article/2014/04/02/us-chile-earthquake-idUSBREA3101G20140402

[13]ITIC,http://itic.ioc-unesco.org/images/stories/list_of_tsunamis/2014/01apr2014_chile/Washington%20Post%20-%20Chiles%20M8.2%20quake%20causes%20little%20damage%20death.pdf