地面效应对超低空空投载机动力学特性的影响

刘日, 孙秀霞, 董文瀚, 李大东, 徐光智

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

0 引言

超低空空投是指利用降落伞等动力减速器在超低空(3～10 m)将重型武器装备、给养等空投至指定区域。在战时部队的秘密集结、突发性自然灾害的救援等诸多领域,超低空空投都扮演着不可替代的重要角色,并逐渐受到部队和专家学者的高度重视[1]。

在超低空空投货物牵引阶段,载机要在极低的高度内完成货物空投。由于地面效应[2]产生的镜像涡系将引起载机的气动特性显著变化,且离地面越近,影响越大。若载机稳定性恶化,将严重危及飞行安全[3]。因此,必须深入分析地面效应对超低空重装空投载机动力学特性的影响。目前,国内外对地面效应的研究主要集中在地效引起的气动力理论计算[4-5]和近地飞行时的稳定性分析[6-7]这两个方面,而针对考虑地面效应影响的超低空空投过程展开的研究才刚刚起步。文献[8-9]通过飞行高度对空投载机气动参数进行补偿,从而将地面效应引入超低空空投过程仿真模型。文献[10]将地面效应和货物移动引起的载机惯性张量的实变等效为气动参数的不确定性,设计了超低空空投纵向反步滑模控制律。文献[8-10]并未系统地研究地面效应对载机动力学特性以及空投任务性能的影响。

本文系统地研究了地面效应影响下空投载机纵向气动特性的变化机理,分析了载机的纵向静、动稳定性,提出了高度模态的飞行品质指标。

1 地面效应对空投载机纵向气动特性的影响

载机超低空飞行时,地面效应对其纵向气动力及力矩的影响主要由以下三部分组成[6-7]:自由涡引起的升力系数变化、附着涡引起的升力系数变化、平尾的升力与下洗角变化。

(1)自由涡引起的升力系数变化

无地面效应影响时,升力系数CL可表示为:

(1)

式中,R为飞机的纵横比,其为翼展bw与机翼面积Sw的函数;CL0为零升迎角引起的升力系数。

地面效应影响下,升力系数变为:

(2)

式中,σ为地面效应影响因子,反映了飞机纵横比的变化,其为飞行高度h(平均气动弦1/4处距地面高度)与翼展的函数。

σ=exp[-2.48(2h/bw)0.786]

(3)

由式(3)可知,当飞机远离地面时,σ→0,即R′→R。

式(2)可理解为在相同的升力系数和离地高度时,地面效应影响下飞机所需的配平迎角减小。

(4)

(2)附着涡引起的升力系数变化

由附着涡引起的升力系数变化量为:

(5)

其中:

(6)

(7)

(8)

(9)

当不使用襟翼与缝翼时,N=N′=1。

(3)平尾升力与下洗角变化

在自由气流中平尾迎角为:

αT=α+φT-ε

(10)

式中,φT为平尾相对机翼的安装角;ε为在自由气流中相同迎角下的下洗角。在地面效应影响下,当翼身组合体升力系数相同时,上式变为:

(11)

式中,Δα为地面效应引起的翼身组合体迎角增量；Δε为地面效应引起的下洗角变化量。

(12)

式中,ε1为在自由流中同一升力系数时迎角α+Δα对应的下洗角;beff为机翼有效翼展;hT为平尾1/4平均气动弦处距地面高度。

由式(1)～式(12)可计算出载机在地面效应影响下的升力、迎角和下洗角的变化量。

在地面效应影响下,某运输机未开启襟翼时的纵向气动力及力矩系数的变化规律如图1所示。

图1 地面效应影响下气动系数的变化规律Fig.1 Variation laws of the aerodynamic coefficients under the influence of ground effect

由图1可知,随着高度的降低,载机的升力系数CL逐渐增大,俯仰静稳定性增强,验证了由理论分析所得的结论。可见,针对超低空重装空投,由于地面效应的影响,升力系数和俯仰力矩系数对高度的气动导数CLh和Cmh不能忽略。

2 地面效应对空投载机纵向稳定性的影响

2.1 地面效应对静稳定性的影响

纵向静稳定性主要指俯仰静稳定性,采用静稳定导数Cmα来衡量。在地面效应影响下,纵向静稳定性除了俯仰静稳定性外,还存在高度静稳定性(Static Height Stability,HS),即当飞机定直平飞时,飞行高度受扰后,其具有恢复原高度的趋势[7]。

高度静稳定性采用升力对高度的导数∂L/∂h来衡量。

(13)

若上式成立,则满足高度静稳定性条件。

在地面效应影响下,配平状态飞机的气动力不仅与迎角有关,而且受到离地高度的影响,CL和Cm的无量纲增量为:

(14)

上式两端消去Δα,得:

(15)

由高度静稳定性条件∂L/∂h<0,得:

(16)

(17)

不同气动布局或不同襟翼开度下的飞机,高度静稳定性均不相同,但由式(16)可知,|CLh|与|Cmα|越大，越有利于高度静稳定性,Cmh越小甚至为负值,越有利于高度静稳定性。

以某型运输机为例,在不同飞行高度、不同飞行速度、不同襟翼开度δf和不同载重情况下的高度静稳定性如表1所示。

表1 不同状态点下的纵向静稳定性Table 1 Longitudinal static height stability at different state points

表1中,mcmax表示最大载重。由表1可知:

(1)在未开启襟翼时,运输机高度静不稳定,并且随着高度的降低,静不稳定性增大,其主要原因在于高度降低时所产生的升力增大量|ΔCLh|/CLh小于低头俯仰力矩增大量|ΔCmh|/Cmh;

(2)襟翼开度越大,载机的高度静稳定性越强,因此,执行超低空重装空投任务时,适度的襟翼开度是有利的。

2.2 地面效应对动稳定性的影响

考虑地面效应影响时,载机纵向运动的特征方程可表示为如下的一般形式[11]:

as5+bs4+cs3+ds2+es+f=0

(18)

式中,特征方程系数a,b,c,d,e,f为气动大导数Xu,Xα,Xh,Zh的函数[11]。为保证在地面效应影响下,载机具有动稳定性,根据Routh-Hurwitz判据,各次项系数须满足以下条件:

(19)

将地面效应影响下的气动大导数带入式(19),由b>0,推出:

(20)

由c>0,推出:

MqZα+XαZu+Mα]/V0

(21)

由d>0,推出:

Mu(Xα-g)

(22)

由式(21)和式(22)可确定出Xh和Zh的范围。

由e>0,推出:

(23)

由f>0,推出:

(24)

由r>0,且不考虑速度变量引起的气动导数变化,可推出:

(25)

联立式(20)～式(25),可确定出保证载机动稳定性的CLh和Cmh取值范围。

以某型运输机最大载重飞行为例,h=10 m,v=80 m/s,δf=50%,可得出保证动稳定性时的CLh和Cmh取值范围,如图2所示。

图2 动稳定性边界Fig.2 Dynamic stability boundary

图2中,阴影部分表示保证动稳定性时的气动导数取值范围。由图2可知,若气动系数落入不稳定区域,表明在此状态点飞行时载机纵向动不稳定。

综上所述,通过设计合理的高度气动导数CLh和Cmh,即配置合理的高度焦点位置,可保证地面效应影响下载机的纵向动稳定。

3 考虑地面效应的超低空空投过程仿真及分析

超低空重装空投牵引阶段,驾驶员执行大的拉杆与推杆动作,以保证载机航迹与姿态的相对稳定。由于尚无相应的国军标品质规范,本节从升降舵效能与空投过程载机响应特性出发,分析地面效应对牵引阶段任务性能的影响。

(1)地面效应对升降舵效能的影响

仿真采用文献[12]的重装空投模型。以某型运输机在低空高度h=100 m,v=100 m/s与超低空h=10 m,v=100 m/s飞行时的升降舵效能进行仿真对比。在1～2 s之间加入1°的升降舵信号,载机的纵向状态量响应如图3所示。

由图3可见,由于地面效应使机翼的下洗减小、平尾升力增加,使得载机升降舵效能降低。而超低空重装空投牵引阶段,驾驶员需要执行大幅、快速的升降舵操纵,抑制货物舱内移动产生的抬头力矩与货物瞬间离机产生的大的低头力矩,升降舵效能降低是极为不利的。

图3 升降舵效能对比曲线Fig.3 Contrast of the elevator efficiency

(2)地面效应对载机动态特性的影响

以下面两个状态点为例进行仿真验证。状态点1:h=10 m,v=80 m/s,δf=50%,引入地面效应的补偿,配平迎角αP=2.525 5°,若此时不考虑地面效应的影响,αP=2.724 3°;状态点2:h=5 m,v=80 m/s,δf=50%,引入地面效应的补偿,αP=2.098 3°,若此时不考虑地面效应的影响,αP=2.718 1°。t=5 s时货物开始在舱内运动,仿真结果如图4所示。图4中,λ为牵引比,圆点表示货物离机时刻,方形表示载机脱离地面效应区时刻。

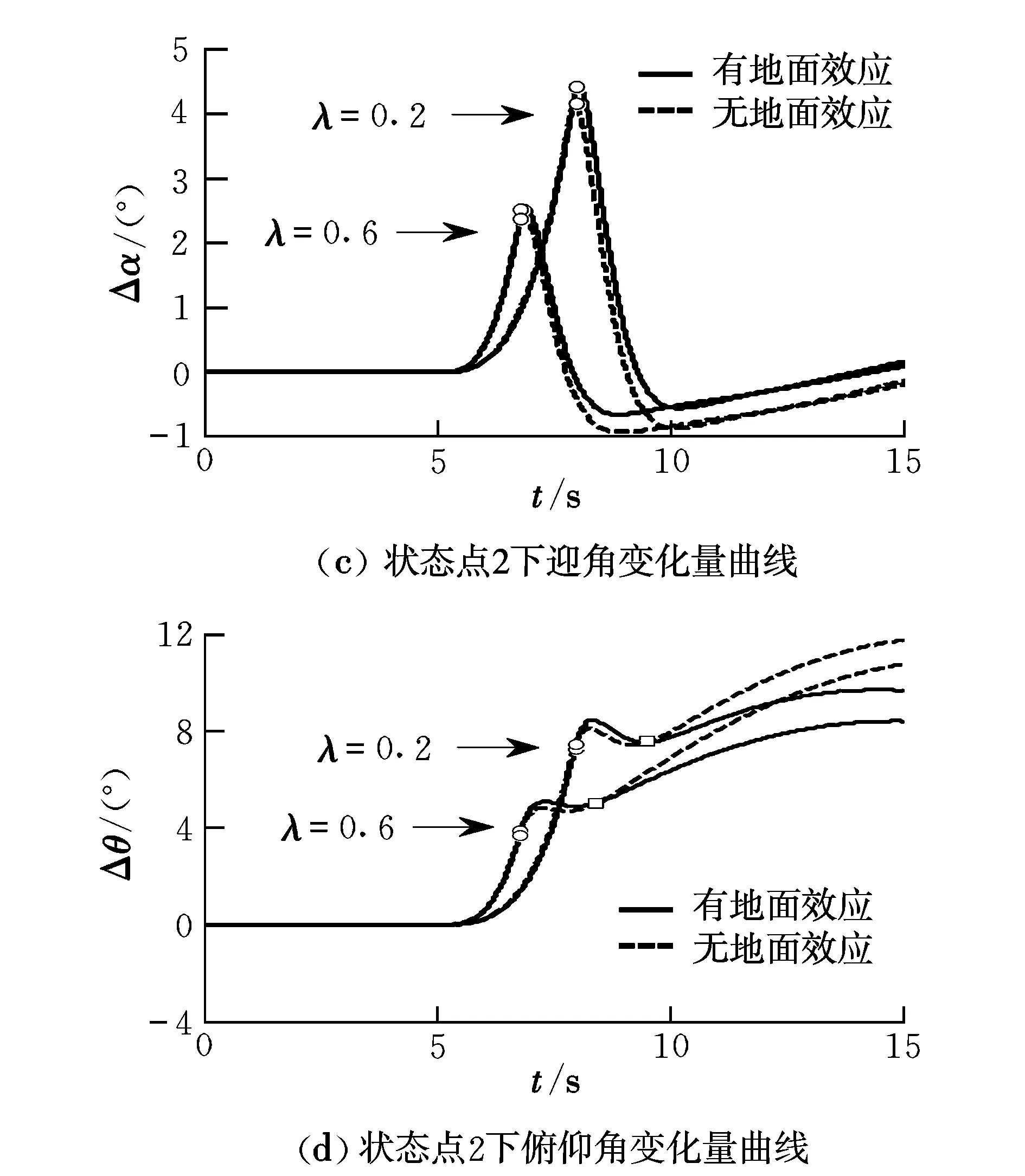
图4 地面效应对货物牵引过程的影响Fig.4 Influence of ground effect on the extraction process

由图4可知,对于状态点1,当λ=0.2时,引入地面效应补偿与未引入地面效应补偿,货物出舱瞬间载机迎角峰值误差Δα=0.114 6°;当λ=0.6时,迎角峰值误差Δα=0.166 2°。对于状态点2,当λ=0.2时,迎角峰值误差Δα=0.326 6°;当λ=0.6时,迎角峰值误差Δα=0.476 0°。地面效应使得载机配平迎角减小,同时使空投过程中俯仰角、迎角响应峰值增大,而且飞行高度越低,这一影响越显著。

4 结论

(1)在地面效应影响下,随着高度的降低,载机的升力系数逐渐增大,俯仰静稳定性增强,而高度静稳定性减弱。

(2)地面效应对载机纵向动稳定性影响较大,但通过设置飞机高度气动焦点位置,可以满足纵向动稳定性要求。

(3)对于常规布局的运输机,地面效应将引起升降舵效能降低,同时使配平迎角减小,空投过程中俯仰角、迎角响应峰值增大。

本文研究结论对执行超低空重装空投任务载机的气动布局设计和任务安全性能评估具有较大的工程实践意义,同时也为超低空重装空投任务指标和操纵品质指标建立打下了坚实的基础。

参考文献：

[1] Michael Henry,Kristen Lafond,Gregory Noetscher.Development of a 2,000-10,000 lbs improved container delivery system[R].AIAA-2009-2909,2009.

[2] 徐华舫.空气动力学基础[M].北京:国防工业出版社,1982:89-92.

[3] 刘日,孙秀霞,董文瀚,等.大气扰动下运输机空投过程建模与仿真分析[J].飞行力学,2013,31(1):24-28.

[4] 李杰,周洲.基于N-S方程的非定常地面效应研究[J].飞行力学,2009,27(1):77-80.

[5] 张西.基于试飞的直升机悬停状态地面效应[J].南京航空航天大学学报,2010,42(2):166-169.

[6] 乐挺,王立新.地效飞机的纵向稳定性和气动布局特点研究[J].飞行力学,2007,25(3):5-8.

[7] Staufenbiel R W,Schlichting U J.Stability of airplanes in ground effect[J].Journal of Aircraft,1988,25(4):289-294.

[8] 刘日,孙秀霞,李大东,等.风场环境下运输机超低空空投安全性研究[J].电光与控制,2013,20(5):25-30.

[9] 仇江,王鑫怡,高亚奎,等.基于自然飞机的超低空重装空投特性分析[J].系统仿真学报,2012,24(4):933-937.

[10] 杨雨,陆宇平.运输机超低空重装空投纵向反步滑模控制研究[J].航空学报,2012,33(12):2301-2312.

[11] 方振平,陈万春.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:250-300.

[12] 李大东,孙秀霞,董文瀚,等.考虑多种影响因素下的改进重装空投系统建模[J].系统工程与电子技术,2013,35(2):447-451.