一类新的Haar子空间中最佳逼近的特征*
方东辉
(吉首大学数学与统计学院,湖南 吉首 416000)
一类新的Haar子空间中最佳逼近的特征*
方东辉
(吉首大学数学与统计学院,湖南 吉首 416000)
研究了广义限制域最佳逼近问题.引入一个L* ̄Haar子空间的概念,刻划了L* ̄Haar子空间中最佳逼近的特征.
最佳逼近;L* ̄Haar子空间;特征

Un(l,u)={p∈Un:l(t)≤Lp(t)≤u(t),t∈K}.
文中均假设Un(l,u)非空.笔者研究间区间为[a,b]的连续函数在Un(l,u)中的最佳逼近的特征问题.对f∈C[a,b],p0∈Un(l,u),称p0为f关于(L;l,u)的广义限制最佳逼近,如果‖f-p0‖=inf{‖f-p‖:p∈Un(l,u)}.
显然,当L为单位算子或导算子时,广义限制最佳逼近问题恰是经典的限制值域和导数值域最佳逼近问题.从20世纪60年代开始,人们对经典的限制逼近问题作了广泛而又深入的研究,参看文献[1-6]及其参考文献.1991年,文献[7]定义了一类新的Harr子空间,即L ̄Haar子空间,并首次对L为一般线性算子时的情况研究了关于(L;l,u)的广义限制最佳逼近的特征刻划等问题.注意到,当L为单位算子时,L ̄Haar子空间与经典的Haar子空间并不等价.针对此问题,文献[8]引进了一类新的Haar子空间,证明了该子空间当L为单位算子时L ̄Haar子空间与Haar子空间的等价性.2004年,文献[9]将优化中的强CHIP性质概念应用到广义限制逼近问题的研究中,刻划了次强内点条件、强CHIP性质和最佳逼近特征之间的关系.笔者在其基础上继续研究这一问题.通过引进文献[8]中的L* ̄Haar子空间,给出了L* ̄Haar子空间中最佳逼近的特征定理,推广了文献[6]中的结论.
1 预备知识
为方便起见,首先引入若干记号.设Z是实Banach空间X的子集,令intZ,coneZ,coZ,|Z|分别表示Z的内部、凸锥、凸包和基数.若Z是凸子集,NZ(z0)表示Z在z0点的法锥,其定义为
NZ(z0)={x*∈X*:x*,z-z0≤0,∀z∈Z}.
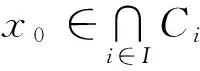
下文中,令X=Un并定义

ex(p)=p(x),Ly(p)=Lp(y) ∀p∈Un.




定义3 称Un为L(或L*)-Haar子空间,如果没有p∈Un{0}在Un的L(或L*)极子集消失.
注1L* ̄Haar子空间由文献[8]所引进.显然,L ̄Haar子空间一定是L* ̄Haar子空间,而L* ̄Haar子空间包含于Haar子空间,因此,{L ̄Haar子空间}⊆{L* ̄Haar子空间}⊆{Haar子空间}.同时,由文献[8]可知,Un为I* ̄Haar子空间当且仅当Un是Haar子空间.
2 最佳逼近的特征
令f∈C[a,b],p0∈Un(l,u),B*是C[a,b]的共轭空间C[a,b]*的单位球.定义
Ωf-p0={x*∈B*:x*,f-p0=‖f-p0‖},
X+(p0)={x∈[a,b]:f(x)-p0(x)=‖f-p0‖},
X-(p0)={x∈[a,b]:(x)-p0(x)=-‖f-p0‖},
K+(p)={y∈K:Lp(y)=L(y)},K-(p)={y∈K:Lp(y)-u(y)},
X(p)=X+(p)∪X-(p0),K(p0)=K+(p0)∪K-(p0),
σ1(f,p0,x)=sgn(f-p0)(x),
定理1 设Un为L* ̄Haar子空间,则{Un,Ct:t∈K}有强CHIP性质.

引理1[3]设P⊆C[a,b]为非空闭凸子集,f∈C[a,b],p0∈P,则p0为f在P上的最佳逼近当且仅当存在x*∈Ωf-p0使得x*,p-p0≤0,∀p∈P.
定理2 设l,u∈C(K),f∈C[a,b],p0∈Un(l,u),Un为L* ̄Haar子空间,则p0为f在Un(l,u)上的最佳逼近当且仅当存在点{x1,…,xs}⊆X(p0),{y1,…,yr}⊆K(p0)(s≥1,s+r≤n+1),常数c1,…,cs,d1,…,dr>0,使得
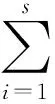
(1)

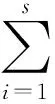
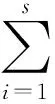
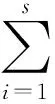
从而,p0是f在Un(l,u)上的最佳逼近.
⟹.设p0为f在Un(l,u)上的最佳逼近.由引理1,存在x*∈Ωf-p0使得
x*,p-p0≤0 ∀p∈Un(l,u).
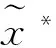
故存在yj∈K+(p0)(j=1,…,m),yj∈K-(p0)(j=m+1,…,r)及常数dj>0(j=1,…,r),使得
(2)
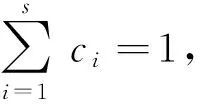
=x*,pexi,p∀p∈Un.
(3)
这样由(2),(3)式得


令p0∈Un(l,u).由文献[9]可知,若intUn(l,u)≠Ø,则{Un,Ct:t∈K}在p0点有强CHIP性质,从而由定理2的证明可知下面结论成立:
推论1[7]设l,u∈C(K),f∈C[a,b],p0∈Un(l,u).若intUn(l,u)≠Ø,则p0为f在Un(l,u)上的最佳逼近当且仅当存在点{x1,…,xs}⊆X(p0),{y1,…,yr}⊆K(p0)(s≥1,s+r≤n+1)及常数c1,…,cs,d1,…,dr>0,使得

[1] SINGER I.Best Approximation by Elements of Linear Subspaces in Linear Spaces[M].New York:Spring ̄Verleg,1974.
[2] RICE J R.The Approximation Functions[M].London:Addison ̄Wesley,1964.
[3] 徐士英,李 冲,杨文善.Banach空间中的非线性逼近理论[M].北京:科学出版社,1997.
[4] CHALMERS B L,TAYLOR G D.Uniform Approximation with Constraints[J].Jber. Dt. Math.-Verein,1979,81:49-86.[5] TAYLOR G D.Approximation by Functions Having Restricted Ranges(III)[J].J. Math. Anal. Appl.,1969,27:241-248.
[6] SHI Yingguang.The Limits of a Chebyshev ̄Type Theory of Restricted Range Approximation[J].J. Approx. Theory,1988,53:41-53.
[8] 王仙云,方东辉.L ̄Haar子空间的性质[J].吉首大学学报:自然科学版,2005(1):12-14.
[9] 方东辉,李 冲,杨文善.强CHIP性质和广义限制域逼近的特征[J].数学学报,2004(6):41-49.
[10] LI Wu,CHANDAL N,SINGER I.Constraint Qualification for Semi ̄Infinite Systems of Convex Inequalities[J].SIAM J. Optim.,2000(11):31-52.
[11] LI C,NG K F,PONG T K.The SECQ,Linear Regularity and the Strong CHIP for Infinite System of Closed Convex Sets in Normed Linear Spaces[J].SAM J. on Optim.,2007,18(2):643-665.
(责任编辑 向阳洁)
CharacterizationoftheBestApproximationonaNewHaarTypeSpace
FANG Donghui
(School of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China)
The problem of the best approximation with generalized restrictions is considered.By introducing a new Haar type space,the characterization of the best approximation is given.
best approximation;Haar type space;characterization
1007-2985(2014)03-0011-04
2014-02-22
国家自然科学基金资助项目(11101186);湖南省教育厅科学研究项目(13B095)
方东辉(1979-),男,湖南洞口人,吉首大学数学与统计学院副教授,博士,主要从事非线性逼近与优化研究.
O174.41
A
10.3969/j.issn.1007-2985.2014.03.003

