微型汽车驱动桥半轴轴承的减摩设计

莫易敏，邱穆红，巫绍宁，高勇，周浩

(1.武汉理工大学 机电工程学院，武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 545027)

对某微型汽车驱动桥进行台架试验时发现，驱动桥的阻力较大，半轴轴承处温升较高；驱动桥启动摩擦力矩的测试结果表明，半轴总成的启动摩擦力矩占驱动桥总成的30%左右，和对标车相比明显偏高，因此有必要对半轴轴承的摩擦力矩进行优化。

国内、外在设计轴承时最关心的是疲劳寿命，由于没有制定相关的摩擦力矩标准，所以几乎都不对其提出要求。国内轴承制造和装配精度与国外相比存在差距，轴承工作时会产生较大的摩擦、磨损和较高的温升，尤其是半轴等承载较大的位置，轴承的摩擦功率损失更为严重，对驱动桥的传动效率会产生一定的影响。随着汽车油耗标准的提高，提高驱动桥传动效率，降低整车油耗尤为紧迫。文献[1]分析了传动系统功率损失的来源，建立了轴承摩擦力矩模型，并对传动系统参数进行了优化，但没有针对轴承本身进行研究；文献[2]通过力学分析建立了轴承摩擦力矩数学模型，但没有将模型应用于试验研究和工程实践中；文献[3]对球轴承沟曲率系数对摩擦力矩的影响进行了理论分析。

下文从半轴轴承设计的角度对轴承的摩擦力矩进行控制。在满足疲劳寿命的前提下，从减小摩擦力矩的角度对轴承结构参数进行优化设计，分析轴承参数对摩擦力矩的影响，并通过摩擦力矩测试和整车油耗与滑行测试验证优化效果。

1 轴承接触理论

假设深沟球轴承没有内部游隙，则对它施加径向载荷时，其载荷区是圆周的一半，各钢球分别承受不同的载荷，设β为钢球之间的夹角，轴承内部载荷分布如图1所示[4-5]。

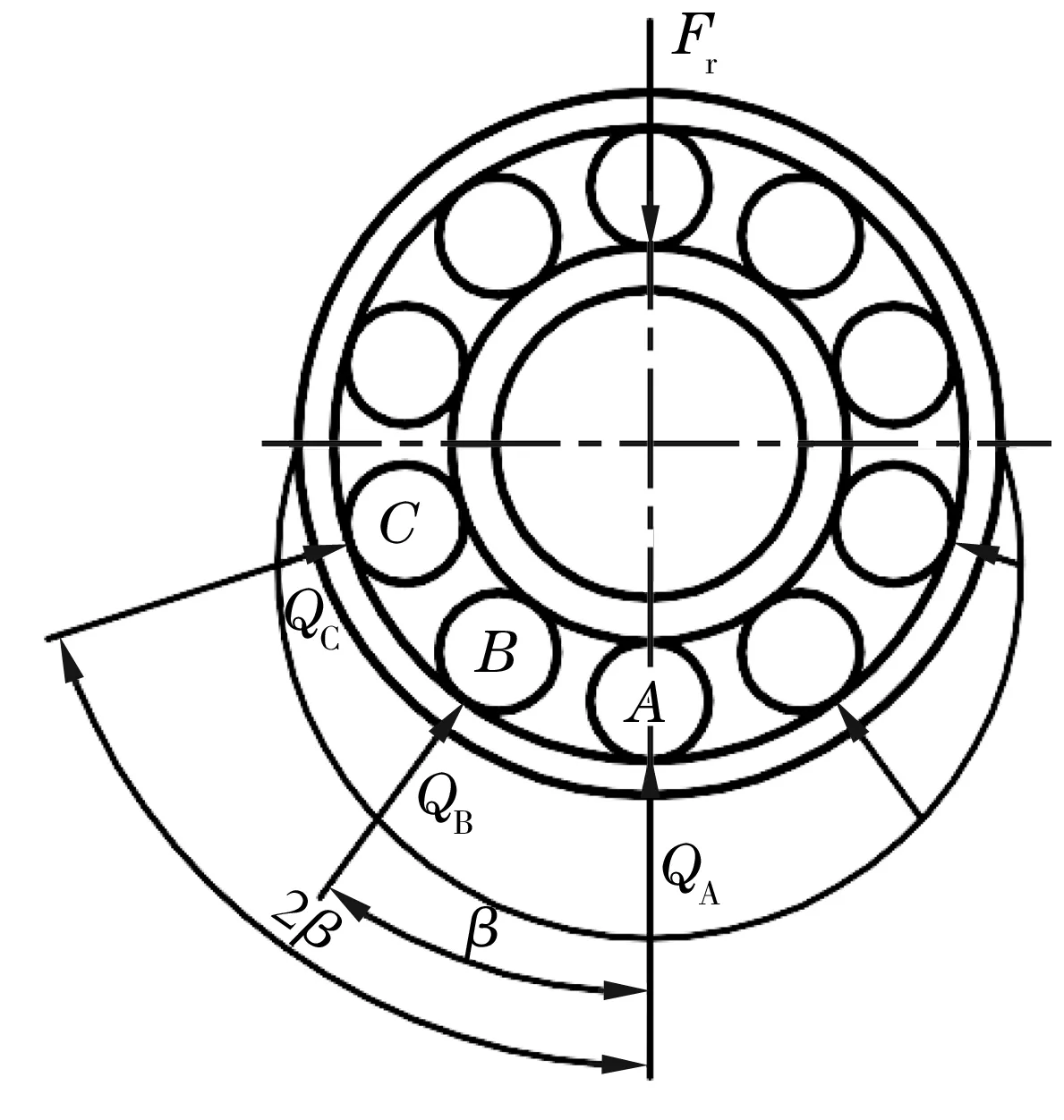
图1 轴承内部的载荷分布

根据Stribeck的推导，有以下关系

(1)

(2)

式中：QA，QB，QC分别为钢球A，B，C与沟道之间的法向载荷；Qi为与钢球A之间夹角为iβ的钢球与沟道之间的法向载荷，i=1，2，…，由于只有一半的钢球承受载荷，所以iβ≤90°；Fr为径向载荷；α为原始接触角；Z为钢球数。

根据Hertz接触理论，内、外沟道主曲率和与曲率函数为[6-7]

(3)

(4)

式中：∑ρ为沟道接触面主曲率和；F(ρ)为沟道接触面曲率函数；f为沟曲率半径系数；Dw为球直径；Dpw为球组节圆直径；上、下运算符分别对应于内、外沟道。

对于钢制轴承，在载荷作用下内、外沟道的Hertz接触椭圆的长、短半轴分别为[6-7]

a=0.023 6a*(QA/∑ρ)1/3,

(5)

b=0.023 6b*(QA/∑ρ)1/3，

(6)

式中：a*，b*为F(ρ)的函数。

2 轴承内部结构参数优化设计

深沟球轴承的内部结构参数主要有球直径Dw，球数Z，球组节圆直径Dpw，内、外圈沟曲率半径系数fi，fe。这5个参数直接决定了球轴承的疲劳寿命、额定动载荷和摩擦力矩等。球数越多，承受载荷的球越多，每个球承受的载荷则越小，沟道接触应力越小；增大沟曲率半径系数，可以增大球与沟道间的接触面积，减小接触应力[3,9-10]，但会增大两者间的滑动和摩擦[3,11]。

2.1 设计变量

以球轴承的5个内部结构参数作为设计变量，表示为

X=[x1,x2,x3,x4,x5]T=[Dw,Z,Dpw,

fi,fe]T。

(7)

2.2 目标函数

以轴承疲劳寿命和摩擦力矩为2个分目标函数，建立数学模型。

2.2.1 疲劳寿命

轴承的疲劳寿命用额定动载荷表示。目标函数取额定动载荷的负值，其表达式为

minf1(X)=min(-Cr)，

(8)

式中：Cr为轴承的额定动载荷。

对于单列深沟球轴承[4]

(9)

(10)

式中：fc为与轴承零件几何形状、制造精度及材料有关的系数。

2.2.2 摩擦力矩

轴承的摩擦力矩涉及弹性力学、接触力学、摩擦、润滑等，且各种因素相互影响，不易进行精确分析计算。这里只讨论钢球与沟道间接触变形弹性滞后引起的摩擦力矩ME和接触椭圆上的差动滑动引起的摩擦力矩MD。

(1)弹性滞后引起的摩擦力矩。由于材料的弹性滞后，钢球在沟道上滚动时产生的滚动摩擦力矩ME为[2]

(11)

式中：η为弹性滞后损失系数，对轴承钢取0.007；K(e)i(e)为第一类椭圆积分，mm；E(e)i(e)为第二类椭圆积分，mm；ai(e)为接触椭圆的长半轴，mm；bi(e)为接触椭圆的短半轴，mm；Eb为钢球弹性模量，N/mm2；Ei(e)为套圈弹性模量，N/mm2；E′为接触面当量弹性模量，N/mm2；ν为泊松比；N为受载球个数；下标i,e分别表示内、外圈。

(2)差动滑动引起的摩擦力矩。由于球与沟道接触椭圆面上各点的线速度不同，从而产生微观滑动，由此产生的摩擦力矩MD为[2]

(12)

式中：fs为滑动摩擦因数，对轴承钢取0.08。

摩擦力矩的目标函数为

minf2(X)=min(Mf)=min(ME+MD)。

(13)

2.3 约束条件

为便于装配，钢球数和球径应满足填球角的要求，可得约束条件

(14)

(15)

式中：ψ0为允许的最大填球角。

钢球直径的选取应符合经验公式，可得约束条件

g3(X)=Kwmin(D-d)-Dw≤0，

(16)

g4(X)=Dw-Kwmax(D-d)≤0，

(17)

式中：Kwmin，Kwmax分别为球径系数的最小值和最大值；d，D分别为轴承内、外径。

为使钢球与保持架相适应，以保证钢球有较好的旋转灵活性，球组节圆直径与轴承平均直径的差应小于规定值，可得约束条件

g5(X)=(0.5-e)(D+d)-Dpw≤0,

(18)

g6(X)=Dpw-(0.5+e)(D+d)≤0，

(19)

式中：e为规定的常数。

内、外圈沟底壁厚应不小于σDw，σ为规定的常数，可得约束条件

g7(X)=σDw-0.5(D-Dpw-Dw)≤0,

(20)

g8(X)=σDw-0.5(Dpw-Dw-d)≤0。

(21)

内、外圈沟曲率半径应不小于0.515Dw，可得约束条件

g9(X)=0.515-fi≤0，

(22)

g10(X)=0.515-fe≤0。

(23)

其中，(14)～(15)式为非线性约束，(16)～(23)式为线性约束。

2.4 最优化算法

轴承内部结构参数优化属于多变量、多目标、多约束的工程最优化问题。实际应用中多采用线性加权法和内点惩罚函数法将优化问题转化为单目标无约束优化问题，间接求解原约束优化问题的最优解。但由于目标函数量纲、数量级等存在差异以及加权系数受设计者主观影响较大，这种方法并不一定能得到全局最优解。

这里应用主要目标法求解多目标函数优化问题，设额定动载荷为第1目标，摩擦力矩为第2目标。对第1目标函数求最优解

(24)

然后增加以下约束条件，对第2目标函数进行优化，作为最终的优化方案,

(25)

式中：Δ1为第1目标函数的允许放宽值[12]。

遗传算法[13]是一种高效、并行、全局的搜索方法，在搜索过程中不易陷入局部最优，而且其适应度函数不受连续可微的约束，广泛应用于各种优化计算中。文中采用遗传算法求最优解，其流程如图2所示[14]。

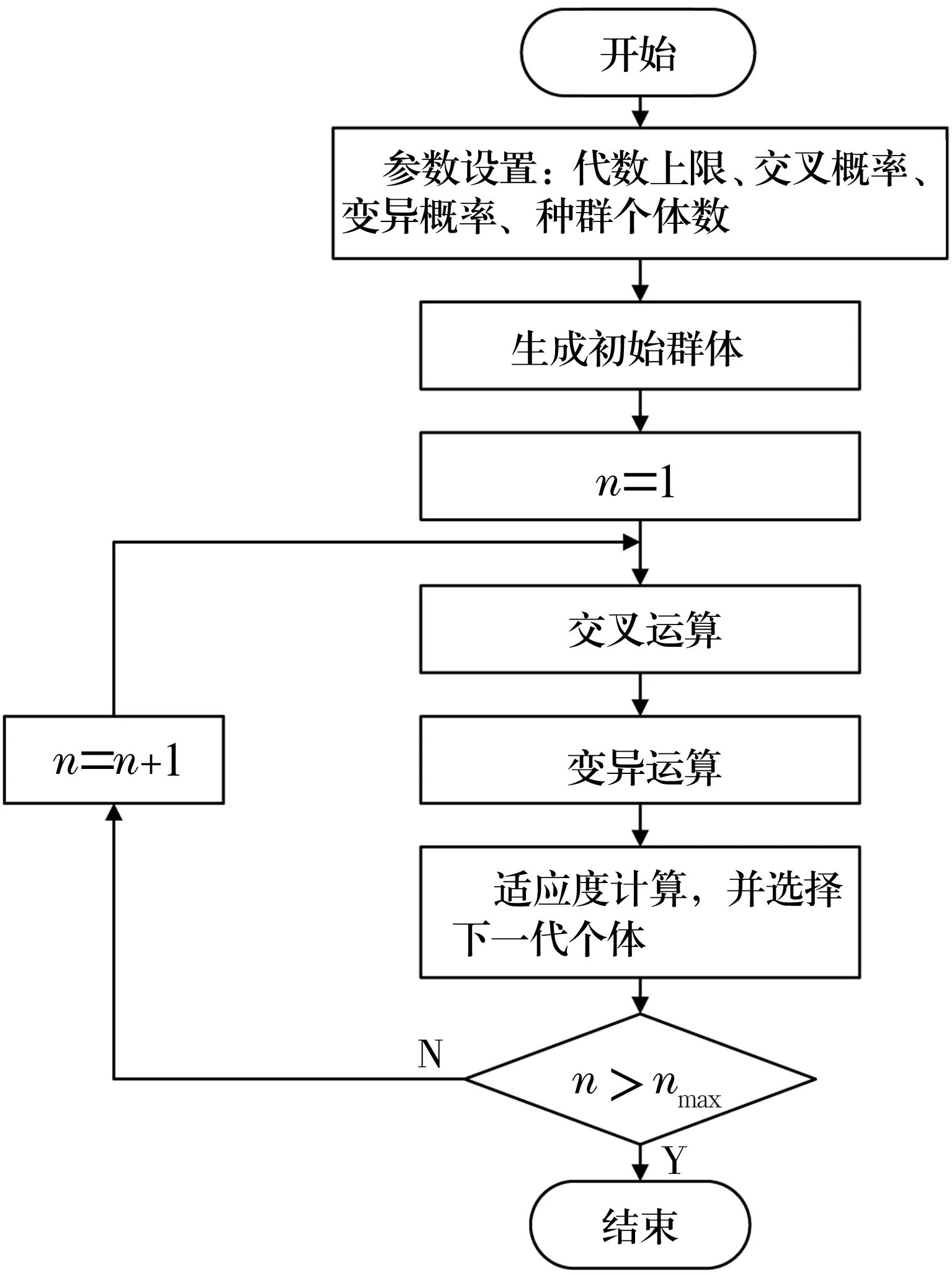
图2 遗传算法流程图

2.5 优化求解

利用MATLAB遗传算法优化工具箱，采用上述目标方程、约束条件以及最优化算法进行求解。基本参数设置如下：d=35 mm，D=80 mm，ψ0=195°，Kwmin=0.24，Kwmax=0.3，e=0.015，σ=0.2，Δ1=3 kN，Fr=5 000 N。

遗传算法参数设置：代数上限100，种群个体数150，交叉概率0.8，变异概率0.2，优化结果见表1。

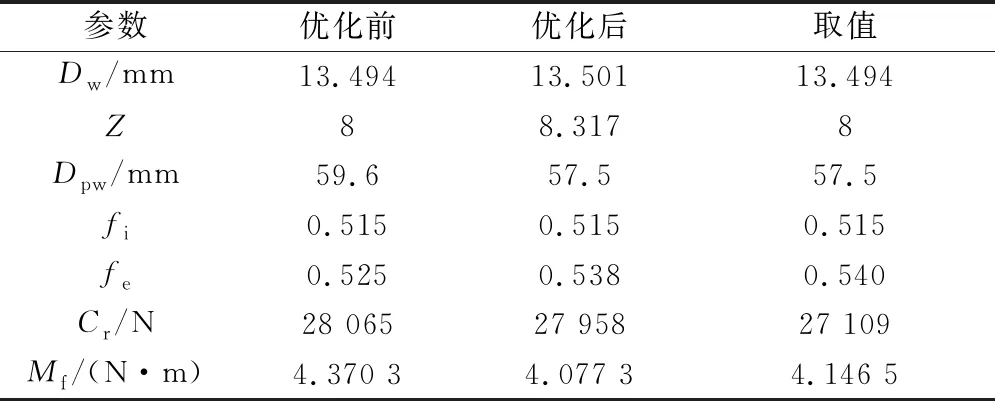
表1 优化结果比较

由表1可知，优化后的球径、球数和内沟曲率系数不变，球组节圆直径变小，外沟曲率系数变大，轴承额定动载荷和摩擦力矩都有所减小。轴承优化后以牺牲较小的额定动载荷改善了摩擦特性。

3 试验验证

3.1 摩擦力矩试验

测量时对轴承施加标准力矩，使其与轴承旋转时产生的摩擦力矩相平衡，此时外加的标准力矩就等于轴承的摩擦力矩。测量采用M9908B摩擦力矩测量仪，其采用低摩擦力矩的空气轴承、精密力矩传感器以及可视化虚拟仪器软件开发的测量系统，人机界面好，测量精度高，技术指标见表2。

表2 M9908B摩擦力矩测量仪技术指标

润滑脂和密封件会对轴承摩擦力矩产生影响，试验时分别测试轴承自身的摩擦力矩以及填脂和安装密封件后的摩擦力矩。为比较轴承结构参数对摩擦力矩的影响，需控制润滑脂和密封件产生的摩擦力矩以保证其一致性。填脂时需严格控制填脂量误差，安装密封件后先在轴承试验机上进行跑合试验，使轴承达到稳定状态，再测试摩擦力矩。选取优化前、后润滑脂和密封件一致性较好的各5套轴承进行测试，测试结果见表3。

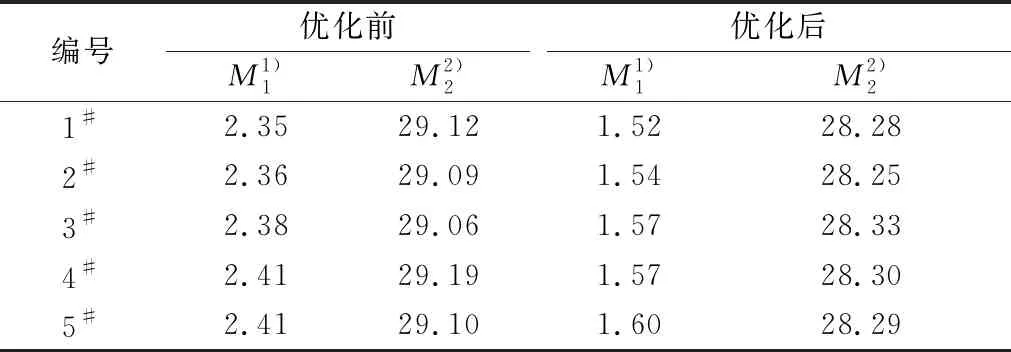
表3 轴承摩擦力矩测试结果比较 N·mm

由表3可知，优化后轴承自身的摩擦力矩有所减小，所选样品轴承填脂和装密封圈后摩擦力矩变化一致性较好。

3.2 整车油耗和滑行试验

依照GB/T 18352.3—2005《轻型汽车污染物排放限值及测量方法(中国Ⅲ，Ⅳ阶段)》和GB/T 12536—1990《汽车滑行试验方法》，在底盘测功机上进行整车油耗和模拟滑行试验。根据装配关系，只需拆掉半轴即可更换半轴轴承，而不会改变汽车其他零部件的状态，测量结果能够反映半轴轴承优化的效果。整车油耗和滑行试验结果见表4。

表4 整车油耗和滑行试验结果比较

由表4可知，尽管整车综合油耗没有变化，但城市和郊区工况油耗都有减小，且滑行距离增加较多，表明轴承结构优化减小了驱动桥阻力。

4 结论

(1)基于遗传算法对轴承内部结构参数的优化表明，在保证轴承疲劳寿命的前提下，通过增大外沟曲率半径，减小球组节圆直径可减小轴承的摩擦力矩；

(2)对优化后的轴承进行摩擦力矩和整车油耗和滑行试验，结果表明，轴承摩擦力矩减小，油耗虽然降低较少，但整车滑行距离得到提升。因此，轴承结构参数的优化可以减小驱动桥的阻力。