激光扫描球形偏心引起误差的理论分析

林静焕，戴 勇，林旭焕，许敏界

（浙江工业大学机电研究所，杭州310014）

激光扫描球形偏心引起误差的理论分析

林静焕，戴 勇*，林旭焕，许敏界

（浙江工业大学机电研究所，杭州310014）

为了研究激光测距扫描仪在测量过程中，由于激光扫描中心与被测球形中心存在一定偏心距时对激光扫描精准度的影响，采用数形结合与公式推导的方法，对偏心距e导致的激光扫描偏差值进行了理论分析，建立了数学模型和公式推算验证，分析了影响激光扫描轮廓偏差几个因素之间的相互关系，得到了当随着半径R增大，偏心引起的误差不会超过的结论。结果表明，通过对提出的偏心误差修正方法进行公式验证，将扫描中心与被测球形中心两坐标轴等效变换至同一坐标系下，可减小偏心距e对激光扫描轮廓造成的偏差影响。

激光技术；基准；偏心距；误差；轮廓扫描

引 言

激光测距扫描仪是集激光测距技术、电子学、计算机技术等学科综合应用的非接触式测量仪器，拥有实时和夜间工作、作业效率高、操作便捷等优势，广泛应用于对物体实时2维或3维轮廓扫描、海洋测绘以及国防建设等领域。

在扫描平面或空间物体内表面轮廓时，激光扫描基准点的选择尤为重要，特别是激光初始点与空间规则物体中心偏心时，便得不到最大截面轮廓，影响激光扫描测量精准度。参考文献［1］中指出激光扫描仪存在一定的误差，误差源主要来自激光光斑、入射角［2］、材料表面反射率等［3］，激光内部因素可通过选择性能优良的仪器进行改善，温湿度以及光线强弱的外部因素影响较小，但对激光扫描空间规则物体的中心偏心这一测量误差并未进行研究分析，实际上对是否可得到最大截面扫描轮廓造成的影响最大［4-7］。

因此，通过对激光扫描球形内表面最大截面测量精准度进行理论分析，建立数学模型并得出了激光扫描与球形中心偏心时造成误差的几个影响因素与相互关系，提出了一种轮廓扫描偏心修正补偿方法，尽量减小形状偏差。

1 激光测距扫描仪工作原理

激光测距扫描装置指一种利用激光测距技术伴随伺服电机转动实现被测物体2维轮廓扫描的仪器［8-10］。它以激光传感器和伺服电机组成的扫描系统为核心，激光扫描装置置于封头中心上方，激光器从被测物体一边缘随着电机进行圆周逐点扫描至完毕，依次测得多点A1，A2，A3，…，An－1，An，利用激光测距至封头表面距离值ρ和电机中光电编码器角度返回值θ，确定各扫描点极坐标值（ρi，θi）（i表示每一个扫描的点，可取i＝1，2，3，…），通过计算机数据处理将各离散扫描点进行最小二乘法拟合，即为激光扫描物体2维形状曲线。如图1所示。

Fig.1 Laser scanning principle

2 激光扫描中心偏心测量误差理论分析

为使激光扫描球形得到最大截面轮廓，必须保证激光扫描中心与球中心一致，但一般而言，很难达到这样的理想状态，总会存在一定偏心距e，造成最大截面轮廓偏差。

如图2所示，O为球中心点，O′为激光扫描中心点，两者偏心距OO′＝e。在理想条件下，球形最大截面曲线和激光扫描曲线会随着偏心距e的大小程度而进行偏移。“⊕”表示拟合曲线在理论曲线上面，偏移量为正；而“⊖”表示为负。两曲线之间的斜线表示偏移值大小，再将各偏移值进行统计带符号计算，表示由偏心距引起所导致的偏移误差值。偏移量e越大，激光扫描球形的截面形状就越小，如图3所示，即偏心距e与扫描截面半径R成反比。因此，必须在测量之前，使“中心”一致或减少偏心距e，保证激光扫描曲线高匹配度。

Fig.2 Deviation chart of theoretical curve and fitted curve

Fig.3 Section contour map under the condition of eccentricity e

3 建立数学模型

在实际工程应用中，激光扫描装置中的电机与球中心在同一平面内，可通过机械方法使电机和球中心保持一致，但激光器与电机是处于正交状态，故激光器与球（电机）中心总会存在一定的偏心距e。建立的数学模型如图4所示。

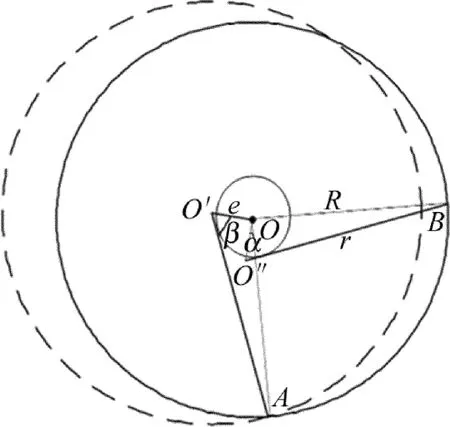
Fig.4 The mathematical model of eccentric measurement

球形最大截面以O为圆心，R为半径的实线圆，虚线表示偏心距e下的激光拟合轮廓；由于激光器和球中心偏心，激光扫描轨迹以球心O为圆心，偏心距e为半径的虚拟圆。其中，O′和O″为转角为α的两激光发射点，对应被测表面扫描点为A和B的偏心角为β。设扫描截面半径为R，测距仪测得值为测量点半径r。

下面对三角形△AOO′进行数学公式推导，根据余弦定理得：

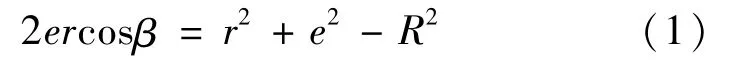
解得：

由于球形最大截面半径无限大于偏心距，且激光测量半径为正，于是得：

3.1 误差分析

（1）针对R，e和β这3个因素来分析激光测量误差的影响。令δ＝r－R，则有：

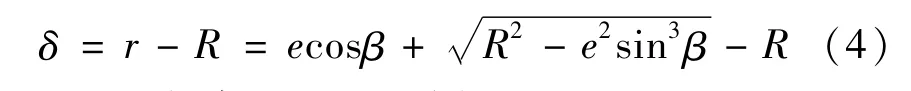
对R进行求导处理，则有：

由上式分析得，dδ＝k·d R（k＞0），误差δ与R成正比，随着R的增大而递增。

因此，在实际现场测量中，激光扫描与球中心偏心距为e时，误差δ的绝对值随着被测圆半径R的增大，其偏心距引起的测量误差不超过

（2）针对被测圆半径R变化时，分析测量误差δ变化的具体情况。

当β∈（0°，90°）∪（270°，360°）时，令δ＝0，可得：

当此时电机回转轴与球形最大截面中心重合时，激光传感器对电机轴中心（球中心）安装偏心对测量内径将不会产生影响。

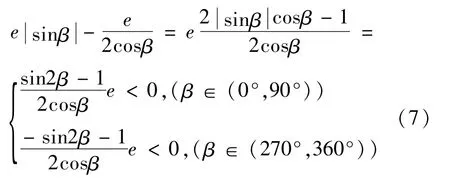
Fig.5 Error curve chart whenβ∈（0°，90°）∪（270°，360°）

当β∈（90°，270°）时，解得：

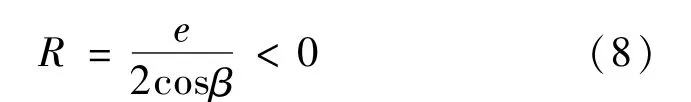
Fig.6 Error curve chart whenβ∈（90°，270°）

通过激光扫描与球中心偏心数学模型的建立与分析，对引起激光测量误差的电机转角α、偏心距e、偏心角β、被测对象圆半径R、激光测距值r等几个影响因素之间关系的数学公式推导，得出了误差δ和的曲线图。随着被测对象圆半径R的变化，激光测距仪安装偏心引起的半径测量误差也会改变，但最大不超过同时，通过控制偏心距e或偏心角β之间的关系变化，达到减小误差的效果。

Fig.7 Error curve chart whenβ＝90°orβ＝270°

3.2 偏心误差修正补偿

为减少由测量中心偏心引起的扫描轮廓偏差，提出一种误差修正方法。设球中心为（xi，yi，0），激光光源中心O′坐标点为（xi′，yi′，0），这里将坐标轴统一至球中心坐标系下，便于软件编译数据处理。则激光中心坐标可表示为：

可经过数学推导将两者不同坐标系进行统一，将激光测量虚拟中心O′进行坐标的转化，重新修正坐标值，减少偏心距对激光扫描球形最大截面轮廓的偏差影响。

4 结 论

为使激光扫描得到球形最大截面形状，必须保证激光扫描与球中心点保持一致，才能实现激光扫描轮廓曲线与理论曲线的高匹配。

（1）在实际测量过程中，激光测量与球中心不一致，扫描轮廓曲线与理论曲线会随着偏心距e的大小程度而偏移，偏差值用两者偏移正负量统计计算而得，扫描得到球形截面半径R与偏心距e成反比。

（2）建立激光扫描偏心距数学模型，得出几个影响激光扫描误差的因素：偏心距e、扫描截面半径R、激光测距值、电机转角等，并分析它们与误差之间的关系；随着R增大，偏心引起的误差不会超过且可通过控制e和β减小误差影响。

（3）提出偏心误差修正方案，通过对两中心点进行等值点转换至同一坐标系，即消除偏心距；再将测量中的各虚拟扫描点重新修正坐标值，减少偏心引起的误差影响。

［1］ DAI J F.Study on 2-D large-scale measurement based on laser range［D］.Tianjin：Tianjin University，2008：28-41（in Chinese）.

［2］ CHEN H，TAN JB.Effect of beam incident angles on trihedral corner reflector laser ranging［J］.Journal of Optoelectronics·Laser，2006，17（8）：986-988（in Chinese）.

［3］ ZHONG Sh Y，LISSh.Study of multi-pulsed laser ranging technology［J］.Laser＆Infrared，2006，36（6）：797-799（in Chinese）.

［4］ WU H Y.Study on large-scale scanning measurement system based on laser range finder［D］.Tianjin：Tianjin University，2009：29-45（in Chinese）.

［5］ DAIBM，ZHANG Ch，LID Sh.Analysis of ranging error of pulse laser ranger［J］.Laser Technology，1999，23（1）：50-52（in Chinese）.

［6］ ZHANG G Y，AN Zh Y，ZHANG C Zh，et al.The laser-scaning proflle auto-measuring instrument and error analysis［J］.Laser＆Infrared，1997，27（2）：88-91（in Chinese）.

［7］ ZHENG D H，SHEN Y Zh，LIU Ch.3-D laser scanner and its effect factor analysis of surveying error［J］.Engineering of Surveying and Mapping，2005，14（2）：32-34（in Chinese）.

［8］ LIU Zh，KRYS D.The use of laser range finder on a robotic platform for pipe inspection［J］.Mechanical Systems and Signal Processing，2012，31（3）：58-63.

［9］ LI J G，LIN Ch J.Based on semiconductor laser technology used in railway detection research［J］.Applied Technology，2010，2（1）：107-108（in Chinese）.

［10］ LI J，WAN Y Ch，JIANG M H.Ground-based laser technology tunnel deformation monitoring technology［J］.Geospatial Information，2012，10（1）：14-17（in Chinese）.

Theoretical analysis of error induced by laser scanning spherical eccentricity

LIN Jinghuan，DAI Yong，LIN Xuhuan，XU Minjie
（Institute of Electrical and Mechanical，Zhejiang University of Technology，Hangzhou 310014，China）

In order to study the effect on the laser scanning accuracy because of a certain eccentricity between the laser scanning center and the spherical test center during the measurement，after setting up a mathematical mode and deducing a calculation formula，the laser scanning deviation caused by eccentricity e was analyzed theoretically.The relationship of the several effect factors of laser scanning contour deviation was analyzed.The conclusion was reached that that eccentricity error does not exceed with the increase of radius R.The results show that the impact of eccentricity e on the laser scanning contour deviation can be reduced after both the axes of the scan center and the measured spherical center are transformed to the same coordinate system equivalently.

laser technique；benchmark；eccentricity；error；contour scanning

TN249

A

10.7510／jgjs.issn.1001-3806.2014.06.019

1001-3806（2014）06-0813-04

林静焕（1988-），男，硕士研究生，研究方向为超精密加工技术。

*通讯联系人。E-mail：b4891392＠163.com

2013-10-14；

2013-11-20