甩挂运输对重型载货汽车气动性能的影响

李 胜， 陈存福， 赵 娥， 胡兴军

(1.一汽解放青岛汽车有限公司， 山东 青岛 266043； 2.吉林大学 汽车工程学院， 吉林 长春 130022)

节能减排与低碳环保已深入到经济生活的每一个角落，商用车运输作为重要的货运方式，在国民经济中发挥着重要的作用.众多运输方式中，甩挂运输因其可有效降低运输成本，减少车辆空驶，提高运输效率而受到各国青睐.甩挂运输在欧美国家已成为主流运输方式，而在我国由于起步较晚，发展较慢.甩挂运输普遍采用“一拖多挂”的运输模式，这会造成同一牵引车配备不同挂车时，主挂车间隙与挂车高度各不相同.

整车行驶过程中，受到气动阻力和滚动阻力的作用，随着车速的增加，气动阻力所占的比重急速上升，油耗增加[1-8].为减小整车气动阻力，国外与部分国内车企在驾驶室顶部安装可调式导流罩，但如何根据货箱高度与间隙大小调节导流罩角度，得到最佳配置，现阶段还没有统一标准.

杜广生等[9]研究了厢式货车间隙长度对气动阻力的影响，指出驾驶室与货箱高度差、间隙均对整车阻力有影响；刘畅等[10]研究了GTS(Ground Transportation System)驾驶室与货箱间隙对气动力的影响，发现间隙长度小于某一特定值时，其对整车阻力系数影响较小，大于此值，阻力系数急速上升；姜辉[11]对厢式货车驾驶室与货箱不同间隙进行了数值分析，得到了初步结论.以上工作均为单独研究间隙与各参数之间的关系，没有考虑各参数之间影响程度的强弱.

本文以间隙、货箱高度与导流罩角度三者为研究对象，利用CFD软件STAR-CCM+对不同间隙长度的整车流场进行数值仿真，得到间隙处的流动状态，分析其流动机理，研究间隙对流场与气动阻力的影响；利用正交试验方法，分析三者之间相互关系，得到影响整车阻力的主要因素，对比优化模型与原始模型，为甩挂运输整车减阻提供理论依据.

1 模型方案

本文研究对象为某一量产重型车，如图1所示.在几何处理中，为保持其形状一致性，保留了关键细节，格栅开口全部保留.整车原始长度为16.4m，驾驶室高度为3.25m，原始货箱高度为4.15m，间隙长度G为2.0m；驾驶室与货箱高度差ΔH为0.9m.

图1 整车尺寸

驾驶室模型分为两类，分别为驾驶室顶部无导流罩与驾驶室顶部装载导流罩.针对无导流罩整车，对3种间隙长度的整车进行数值模拟，带导流罩整车设置7种间隙长度进行分析，对比其流场结构，参数设置见表1.

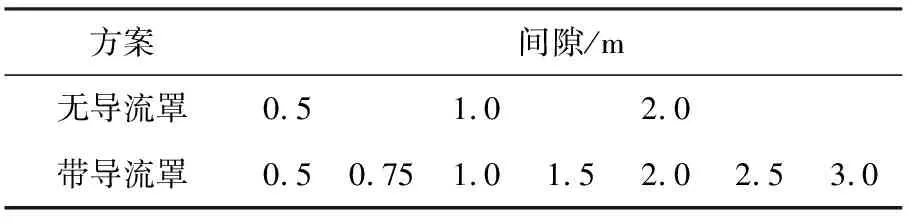
表1研究方案

2 数值模拟

2.1计算域尺寸

由于车体表面结构复杂，一般软件较难捕捉表面细节，故采用STAR-CCM+对模型进行网格包面、重构以及体网格划分.在计算中，采用1∶1比例模型.为满足计算条件，计算域应足够大，以便施加入口和出口边界条件后，计算域对整车流场的影响较小.入口边界距车前为2.5倍车长，出口边界距车尾4.0倍车长，两侧取5倍车宽，顶部取4倍车高，计算域模型大小如图2所示.

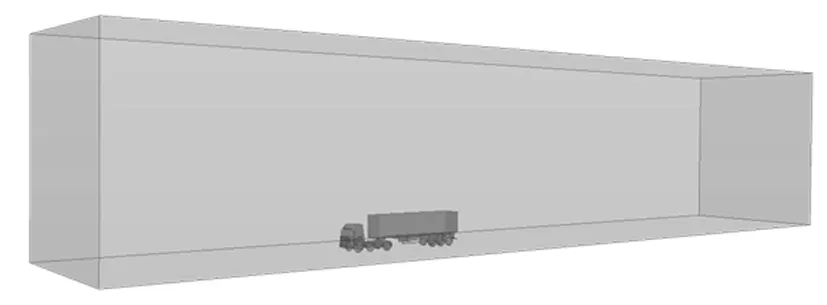
图2 计算域示意图

2.2网格模型

基于对流动细节的捕捉，本文对整车表面设置边界层网格，并对车体后视镜、底盘、尾部等重点区域进行了加密，体网格类型采用多面体网格.最终，网格数量达2 500万，满足了计算需要.流场中截面网格如图3所示.

图3 中截面体网格

2.3湍流模型与边界条件

为更好地捕捉流场结构，在计算中采用了SST k-ω模型.SST k-ω结合了k-ε与k-ω计算特点，在近壁面保留了原始的k-ω模型，远壁面采用k-ε模型.SST k-ω模型通过一个混合函数实现从近壁面k-ω模型到远壁面k-ε模型的过渡，该混合函数以壁面距离和湍流量为参数[12-13].

设定整车行驶速度为30m/s，环境温度为20℃，此时马赫数为0.088，远低于0.3，因此可认为空气处于不可压状态，流场边界条件如表2所示.

表2流场边界条件

3 结果与讨论

3.1间隙G对整车气动特性的影响

前后压差阻力是重型载货汽车阻力的主要来源，约占汽车总阻力的50%～65%，其余为摩擦阻力、诱导阻力与整车内阻[14].由于压差阻力比重大，在整车减阻设计中，可通过降低压差阻力，达到降阻的目的.

图4为无导流罩整车在三种不同间隙下的阻力系数变化趋势，其中整车阻力系数为货箱与驾驶室阻力系数之和.由图4可知，随着间隙的增加，整车阻力系数上升；货箱阻力系数的变化趋势不明显，驾驶室阻力系数呈增大趋势.间隙增加，导致驾驶室后部尾流区发展更为充分，形成较强漩涡，消耗较多能量，产生较大负压，使驾驶室前后压差增加.

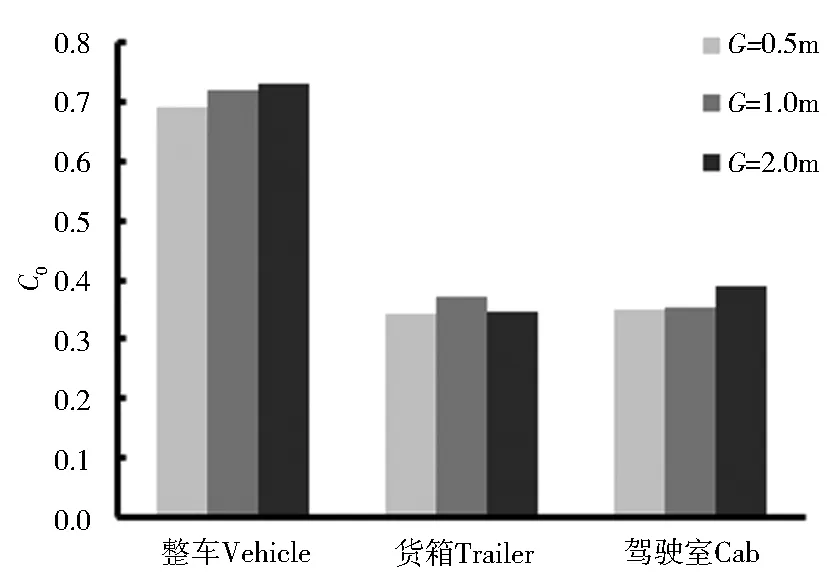
图4 不同间隙下无导流罩整车阻力系数

图5表示相对于原车配置阻力系数变化趋势，主挂车间隙为0.5m时，减阻比例可达5.7%，效率相当可观，改变间隙对整车气动阻力的影响不可忽视.

图5 不同间隙下阻力系数变化趋势

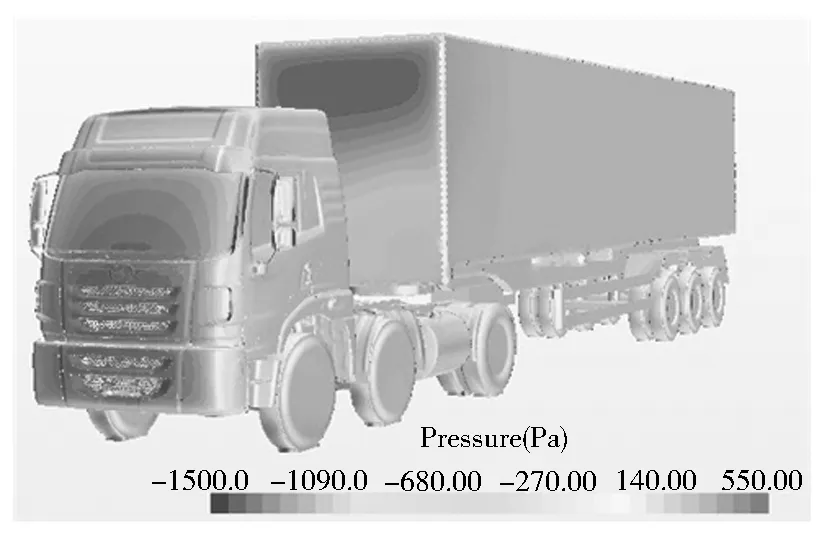
图6 整车表面压力分布(G=2.0m)

图6表示间隙距离为2.0m时整车压力分布云图，由图6可以看出，驾驶室前脸格栅处、挡风玻璃下部、后视镜前部、货箱迎风面上缘、车轮下部均受到较大的正压作用；驾驶室A柱、后视镜边缘受到的压力较小，这是由于此处空间突然增大，气流速度急剧增加，由伯努利方程可知，此处受到的静压较小.

图7为货箱正面压力分布云图，可知三者上方均受到较大的正压作用，受压面积基本一致.产生此现象的原因是驾驶室与货箱存在高度差，流经驾驶室顶部的气流冲击货箱顶部，气流遇到阻碍，速度减小，动能转化为作用于货箱顶部的正压能.货箱前移，受压面积并未发生较大改变，证明气流并未在驾驶室顶部发生分离.

(a)G=0.5m (b)G=1.0m (c)G=2.0m图7 三种间隙下货箱正面压力分布

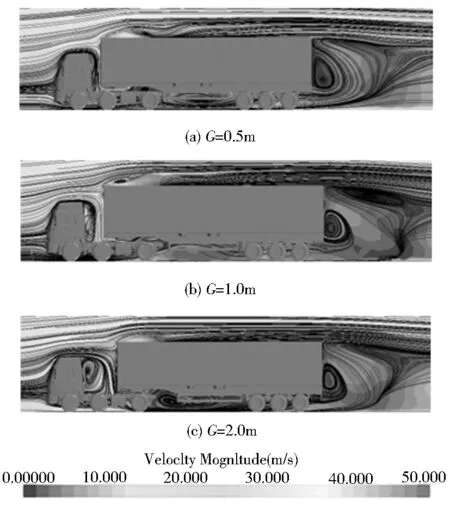
图8 三种间隙下中截面流线分布

图8显示了三种不同间隙中截面速度流线分布，前方气流遇到驾驶室的阻挡，一部分气流沿着挡风玻璃等向上爬升，一部分气流绕过前保险杠向驾驶室下方流去，其余气流沿着驾驶室侧面向后流去；流经驾驶室顶部的气流遇到货箱的阻碍，在货箱顶部发生流动分离，一部分气流沿着货箱向下流动，流入底盘，另一部分绕过货箱拐角，向后流去，汇入尾流区；由于间隙不同，在间隙处形成的涡流出现差异.G=0.5m时，驾驶室后部漩涡较小，没有充分发展；G=2.0m时，驾驶室后部形成明显的漩涡，漩涡的旋转摩擦，消耗了大量的能量，造成驾驶室后部压力降低，造成驾驶室前后压差增大，这也是间隙大、驾驶室阻力增加的原因.

主挂车间隙大，流入底盘处的气流也相对较多，对底部的冲击作用也相对较强，也一定程度上增加了阻力.在三种间隙下，货箱尾部均形成明显涡旋，其中G=1.0m时，下旋漩涡明显较其他两者突出，由此可知，间隙的大小可造成尾流结构的不同.

图9所示为高度为2.15m处间隙速度矢量分布，由图9可知，间隙较小时，漩涡体积较小，数量较多，流动较为紊乱；随着间隙的增加，漩涡轮廓逐渐清晰，G=2.0m时，漩涡数量变为2，漩涡中心后移，逐渐向尾流形态发展；驾驶室后部漩涡受到货箱阻挡，有向外发展的趋势.

图9 高度为2.15m水平截面速度矢量分布

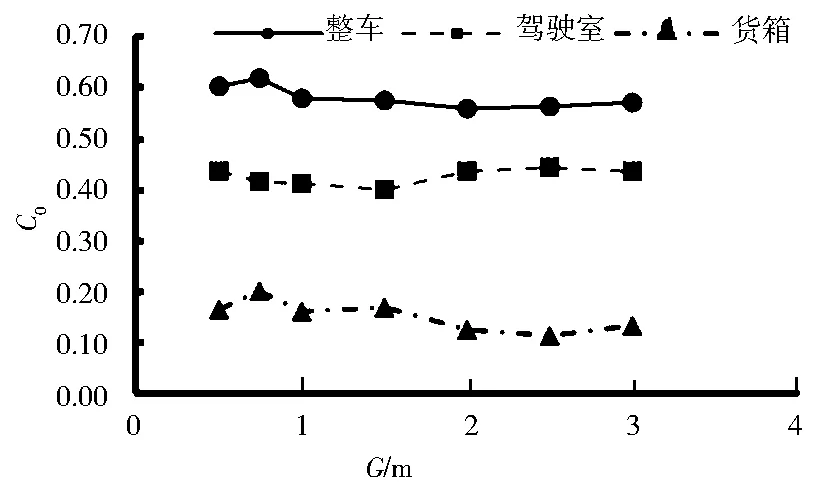
图10 不同间隙带导流罩整车各部分阻力系数

3.2间隙G对带导流罩整车气动特性的影响

图10是带导流罩重型载货汽车在不同间隙下的阻力系数分布.由图10可知，加装导流罩后，整车阻力系数并不像无导流罩时阻力系数变化趋势一致，而是呈现出新的特点：随着间隙的增加，阻力系数减小，到达特定值后，又缓慢上升.对于本车，在G=2.0m时阻力系数最小.其中驾驶室阻力系数与货箱阻力系数呈现出近似相反的变化关系.

图11为相对于G=0.5m时整车气动阻力系数的变化值，G=2.0m时整车阻力系数减小7%；随着间隙的增加，减阻效果减弱，G=3.0m时，减阻比例下降至5.3%.图11表明，对于同一种整车配置，在不改变导流罩形式及安装方式的工况下，有一个最佳间隙，与文献[15]结论一致；最佳间隙下，阻力系数可达到最小.

图11 不同间隙减阻比例(相对于G=0.5m车型)

图12 不同间隙下中截面流线分布

图12表示不同间隙下带导流罩整车中截面速度流线，图中选取四种间隙整车流场进行对比分析，间隙分别为0.5m、1.0m、1.5m和2.5m.由图12可知，随着间隙的增加，驾驶室后部产生的漩涡体积逐渐增大，涡核位置后移；大漩涡消耗了大量的能量，降低了驾驶室后部的压力，使驾驶室阻力有不同程度的增加.

日本学者武藤真理[16]提出气流“折射”的概念，当间隙过短或过长时，会出现“折射不足”或“折射过分”的现象，使整车阻力增加.为降低整车阻力，必须使驾驶室顶部流线折射适当.由以上分析可知，适当调节导流罩安装角度可改变驾驶室顶部流线，使之达到合理折射.

现阶段，为节约成本，国内厂家生产的导流罩大多为固定式，主挂车匹配方式改变时，导流罩角度不能随之调节，驾驶室顶部气流得不到有效理顺.当主挂车高度差较大时，驾驶室顶部气流会直接冲击挂车前部，造成气动阻力增加，增加整车油耗，引起运输成本上涨.为降低运输成本，导流罩可设计为角度可调式，根据货箱高度，调整不同角度，降低整车气动阻力.

图13为装载导流罩整车在水平高度为2.15m处的速度矢量图.与无导流罩间隙处流态相似，间隙较小时，涡旋较多，流动较为复杂；随着间隙的增大，流动逐渐稳定，漩涡个数由多个向两个发展；间隙为3.0m时，间隙处的流动呈现出尾流流动特性.由于驾驶室两侧增加了侧导流板，来自于驾驶室侧面的气流在侧导流板的引导下没有直接冲击货箱两侧，这也起到了一定的减阻作用.

图13 高度为2.15m间隙处水平截面速度矢量

3.3三因素正交试验

正交表是进行正交试验设计的基本工具，等水平正交表一般为La(bc)，其中a为试验次数，b为因素水平数，c为列数[17].本文选取影响整车阻力的导流罩角度A、间隙B与货箱高度C为正交试验的因素.原车导流罩角度、间隙与货箱高度分别为25°、2.0m与4.15m.由于试验次数不宜过多，每个因素均取3个水平，根据国家标准及整车外形参数，取对应水平表如表3所示.

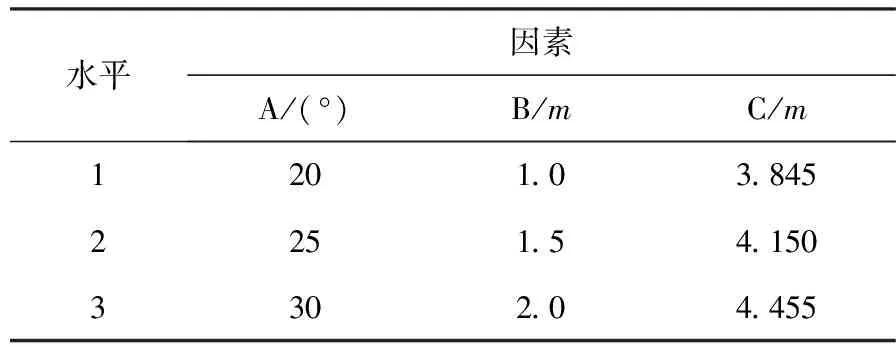
表3各因素对应水平

根据试验原则，选用的正交表类型为L9(34)，对试验方案进行9次仿真分析，结果如表4所示，其中D列为空列.

由试验结果可知，三种试验因素的影响程度由大到小依次为C>B>A，通过比较各组合均值可得到最优组合为A3B3C1，即导流罩角度为30°，间隙为2m，货箱高度为3.845m，此时阻力系数最小，仿真结果为0.546.原始车型阻力系数为0.560，优组合整车减阻率为2.5%，验证了试验分析的正确性.

表4L9(34)正交表与模拟结果

为验证模拟结果可信度，对正交试验进行方差分析，得到正交试验结果的方差分析表，如表5所示.

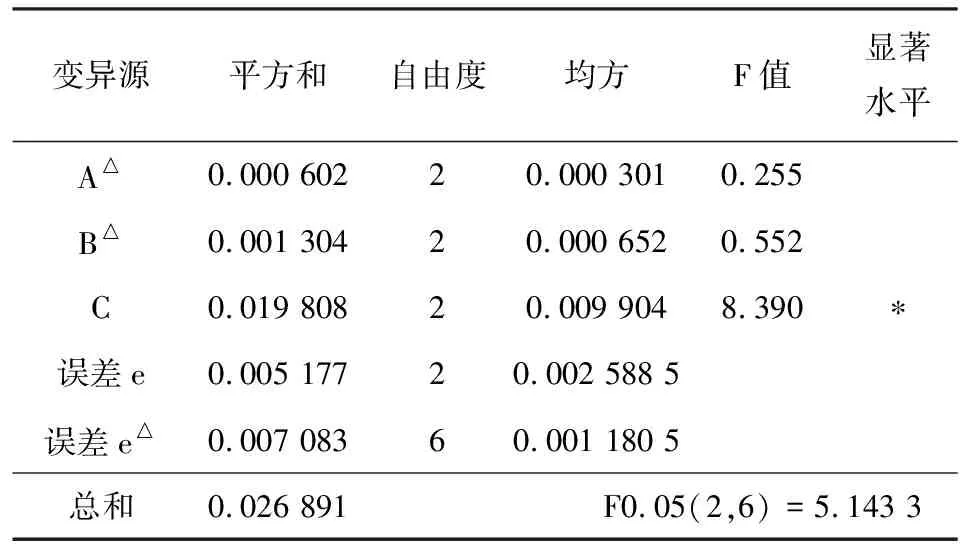
表5方差分析表

显著性检测显示，货箱高度对阻力系数的影响较为显著，置信度高达95%；其余两者对阻力系数的影响不显著.

4 结束语

利用数值模拟方法计算了甩挂运输中不同参数下对整车气动性能的影响，揭示了甩挂运输中整车外流场的流动机理，得出以下结论：

(1)对于无导流罩重型载货汽车，间隙增加导致整车阻力系数升高；增加的间隙使驾驶室后部尾涡扩展，增大了驾驶室阻力.

(2)导流罩角度与挂车确定时，存在最佳间隙，此时整车阻力系数最小；实际运输中，增大或减小相同高度货箱间隙，需适当减小或增大导流罩角度.

(3)正交试验可有效分析各因素影响程度及各因素最优组合，得到整车最低阻力系数，为车辆气动特性优化提供指导.

(4)在甩挂运输中，需根据间隙、货箱高度调节导流罩角度，使牵引车与挂车相匹配，降低油耗.

[1]Committeetoassessfueleconomytechnolo-giesformedium-andheavy-dutyvehicles.Technologiesandapproachestoreducingthefuelconsumptionofmedium-andheavy-dutyvehicles[M].WashingtonDC:NationalAca-demiesPress, 2010.

[2] 张伟.EQ1118GA运输车外流场的数值模拟与分析[D].杭州：浙江大学，2006.

[3] 王靖宇，胡兴军，田华，等.导流罩对轻型厢式货车气动特性影响的数值模拟[J].吉林大学学报：工学版，2008，38(1)：12-16.

[4] 王牧.某商用车导流罩造型与阻力系数关系的研究[D].长春：吉林大学，2009.

[5] 王新宇，胡兴军，李腾飞，等.新型裙板对重型车气动特性的影响[J].吉林大学学报：工学版，2012，42(1)：37-40.

[6] 龚旭，谷正气，李振磊，等.基于代理模型的集装箱载货车侧风下气动阻力的优化[J].汽车工程，2012，34(2)：133-137.

[7] 王新宇，王登峰，范士杰，等.商用车空气动力学附加装置减阻技术的研究及应用[J].机械工程学报，2011，47(6)：107-112.

[8〗 徐佳奕.某载货汽车空气动力学减阻研究[D].长春：吉林大学，2007.

[9] 杜广生，王德昌，雷丽，等.厢式货车尾流特性的分析[J].农业机械学报，2002，33(5)：27-30.

[10] 刘畅，王靖宇，桑涛，等.大型载货汽车驾驶室与货箱间隙对气动特性的影响[J].吉林大学学报：工学版，2007，37(2)：280-285.

[11] 姜辉.厢式货车气动减阻技术的数值模拟[D].南京：江苏大学，2007.

[12] 胡兴军，李腾飞，王靖宇，等.尾板对重型载货汽车尾部流场的影响[J].吉林大学学报：工学版，2013，43(3)：595-601.

[13]MenterFR.Zonaltwoequationk-wturbulencemodelsforaerodynamicflows[C]//AIAA.24thFluidDynamicsConference.Orlando:NASA-AmesResearchCenter, 1993,1-21.

[14] 姜波.货车尾随行驶外流场计算模拟及其燃油经济性分析[D].长沙：湖南大学，2007.

[15] 杜广生.厢式货车空气动力学特征的研究[D].上海：中国船舶科学研究中心，2002.

[16] 武藤真理.汽车空气动力学[M].长春：吉林科学技术出版社，1989.

[17] 宋涛.基于试验优化设计的重型商用车气动减阻技术研究[D].长春：吉林大学，2011.