非均匀核物质状态方程研究

张肇文 申 虹

（南开大学 物理科学学院 天津 300071）

非均匀核物质状态方程研究

张肇文 申 虹

（南开大学 物理科学学院 天津 300071）

在相对论平均场理论框架下研究非均匀核物质，自洽的Thomas-Fermi近似是一种有效的方法。这种方法假设了非均匀核物质是由原子核及核外中子气和质子气构成。在温度T、质子分支比Yp以及重子密度ρB确定的情况下，通过改变Wigner-Seitz原胞半径，对系统的每重子自由能进行最小化，从而得到热力学稳定态，原胞内的重子分布也可以自洽地得到。由自洽的Thomas-Fermi近似得到的结果可以与之前工作所得到的结果进行详细比较，之前的工作所采用的是参数化的Thomas-Fermi近似方法。

非均匀核物质，状态方程

高温致密物质的状态方程对于研究天体物理现象非常重要，例如：超新星爆发和中子星形成[1-4]。核物质状态方程是超新星爆发研究的重要输入量，由于超新星爆发过程的复杂性，使得描述系统的核物质状态方程十分复杂。目前被广泛采用的状态方程有采用液滴模型构造的状态方程[5]，以及采用Thomas-Fermi近似方法构造的状态方程[4,6-7]和采用自洽相对论平均场计算给出的状态方程[8]。本文采用了自洽的Thomas-Fermi近似与相对论平均场理论相结合的方法来处理非均匀物质相。

自洽的Thomas-Fermi近似方法所给出的原子核的性质与实验数据非常接近[9]。最近，Thomas-Fermi近似方法被用于研究在亚核密度下原子核的pasta相的性质[10-11]。我们前期工作中[12]，参数化的Thomas-Fermi近似只考虑了droplet相。本文通过对比核子分布以及热力学量来检验自洽的Thomas-Fermi近似(STF)与参数化的Thomas-Fermi近似(PTF)的区别。另外本文还考虑了bubble相所带来的影响。

关于有效的核相互作用，我们采用了相对论平均场理论(Relativistic Mean Field, RMF)，核子之间通过交换介子发生相互作用，其中介子包括了标量-同位旋标量介子σ、矢量-同位旋标量介子ω以及矢量-同位旋矢量介子ρ。本文采用了TM1参数组[11]，它能给出很好的有限核的基态性质，并且预言中子星的质量上限为2.18 M⊙。 另外在前期的工作中，PTF的计算也是将TM1的结果作为输入量，因此可以在相同的RMF理论中对STF和PTF进行详细的对比。

1 理论模型

对于均匀核物质，我们采用RMF理论来计算其性质，对于非均匀核物质相，由于原子核的存在而使得系统的自由能降低，我们采用STF近似方法来得到场的运动方程。

在RMF理论中，由质子、中子和电子组成的系统，它的拉氏密度为：

式中，Wμν、Raμν和Fμν分别是ωμ、ρaμ以及Aμ的全反对称张量，所采用的TM1参数组由表1给出。

表1 TM1参数组(MeV)Table1 Parameter set TM1 (MeV).

从拉氏密度式(1)出发，得到一组Euler-Lagrange方程。在RMF近似下，介子场可视为经典场，可以由它们的期望值所代替，其运动方程由式(2)-(5)给出：

式中，in和,sin分别是粒子种类i的粒子数密度和标量密度，它们由式(7)、(8)给出。核子满足以下方程：

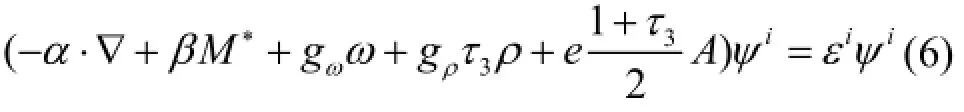
式中，M*=M+gσσ是核子的有效质量。

非均匀物质相由Wigner-Seitz近似描述，核物质分布于电中性的球形Wigner-Seitz原胞中，原胞内的核子密度分布由STF近似给出，核子密度通常是径向坐标r的函数。在STF近似中，系统的状态由热力学平衡条件确定，这给出了平均场满足的方程(2)-(5)，粒子及反粒子在各能级上的占据几率见式(9)、(10)。通过自洽求解这些耦合方程，可以确定系统的热力学平衡状态及其性质。在Wigner-Seitz原胞中，核子在坐标r处的粒子数密度和标量密度分别为：

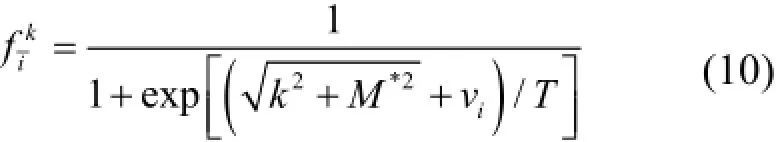
化学势iμ与有效化学势iν的关系是：

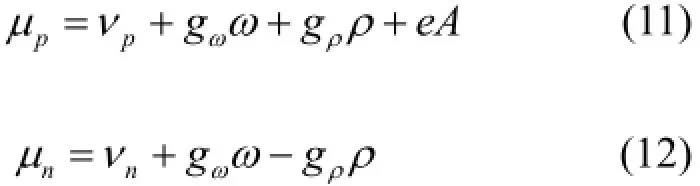
在给定Wigner-Seitz原胞半径及重子密度和质子分支比的情况下，具体的求解过程如下：首先给出介子场的初始猜测，通过给定的质子数和中子数确定相应的化学势，当化学势确定后，就可以求得系统的各类密度分布，再将得到的密度分布代入介子场方程，从而得到新的介子场。这一自洽求解过程迭代数次，直至得到收敛的介子场和核子密度分布。得到自洽解后，则可以计算得到系统的热力学性质。Wigner-Seitz原胞半径通过自由能密度最低条件确定。通常可以假设电子是均匀分布的，由于电子不参与自由能最小化的过程，我们在这里不包括电子的贡献。核子的能量密度和熵密度为：

在自由能最小化的过程中，还需要考虑体心晶格的库仑能修正项CEΔ[12]，这一修正对于bubble相和droplet相有所不同[13]。

PTF近似方法假设了核子在Wigner-Seitz原胞中的分布具有如下形式：

在温度T、重子密度ρB以及质子分支比Yp固定的情况下进行自由能最小化。ρB和Yp为原胞内的平均值，由式(16)、(17)给出：

2 结果与讨论

在关于非均匀核物质相的研究中采用STF近似，同时考虑了droplet相和bubble相，并与均匀相的结果进行比较，从而确定具有最低自由能的稳定态。结果表明，在靠近非均匀-均匀相变点密度附近，bubble相比droplet相具有更低的每重子自由能。

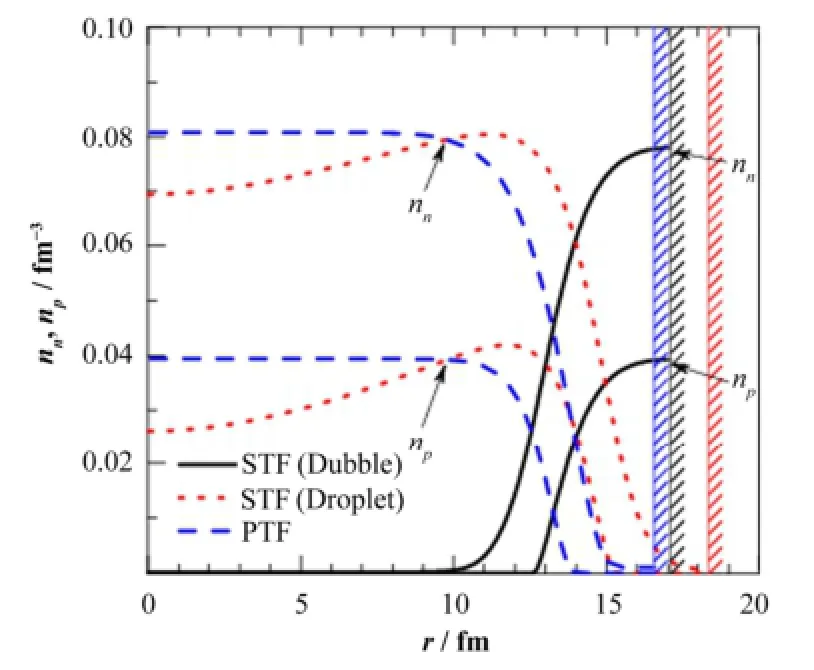
图1 在T=1 MeV、ρB=1014 g.cm-3、Yp=0.3情况下Wigner-Seitz原胞内质子和中子的密度分布Fig.1 Density distributions of protons and neutrons inside the Wigner-Seitzce14ll forth-3e case of T=1 MeV, ρB=10 g.cmand Yp=0.3.

图1 给出了在Wigner-Seitz原胞内质子与中子的密度分布，分别给出了在STF近似中得到的droplet相（点线）和bubble相（实线）以及在PTF近似中得到的droplet相（虚线）。在STF近似中，原胞中心区域的密度明显比表面区域低，这是因为库仑相互作用将更多的质子推到表面。在PTF近似中，由于核子密度分布被限定为式(15)的形式，因此没有出现这种现象。在重子密度附近，bubble相具有比droplet相更低的自由能，因此考虑了bubble相之后，会提高非均匀-均匀相变密度。例如，在重子密度、Yp=0.3和T=1 MeV情况下，在droplet相与 bubble相和均匀相之间，每重子自由能最低的态是bubble相，但是如果不考虑bubble相的话，均匀相的每重子自由能最低。

图2给出了每重子自由能F随重子密度的变化，其中STF近似的结果用实线表示，PTF近似的结果用虚线表示。我们发现两种方法得到的结果存在微小的差别，这是因为它们处理表面效应和核子密度分布的方法不同。在STF近似中，原子核的表面效应和核子密度分布通过自洽求解得到，由于密度分布不均匀导致的表面能（梯度能）包含在式(13)中，无法将其与体积能分离开，这样的关于表面能的处理是自洽的，没有引入更多的近似和参数。另一方面，在PTF近似中，每个原胞的表面能无法自洽求解得到，假设其具有形式为，其中0F= 70 MeV.fm5为引入的模型参数。如图2所见，PTF给出的每重子自由能结果小于STF的结果，这主要是因为PTF中所采用的参数F0较小导致。由于采用了较小的F0，低估了表面能的贡献，从而使PTF给出的每重子自由能偏低。除此之外，由图2看到，在重子密度ρB＞1013.9g.cm-3时，由于bubble相的存在，使得系统的每重子自由能明显降低。

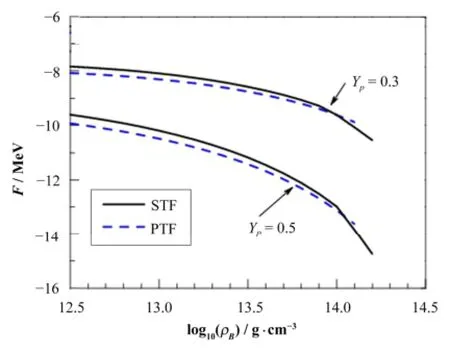
图2 在Yp=0.3和0.5、T=1 MeV情况下每重子自由能F随重子密度ρB的改变Fig.2 Free energy per baryon F vs. ρB for Yp=0.3 and 0.5 at T=1 MeV.

3 结语

我们采用STF近似和RMF理论对非均匀核物质进行了研究，并将结果与前期工作中的PTF近似得到的结果做了详细的比较，另外我们还考虑了在非均匀-均匀相变之前可能出现的bubble相的影响。

在STF近似中，核子密度分布和表面能由自洽求解得到，通过调节Wigner-Seitz原胞半径对系统自由能进行最小化，并且同时考虑了droplet相和bubble

相。在与PTF近似结果对比后，我们发现两种近似在低密区域，核子密度分布并没有显著差别，但是在靠近非均匀-均匀相变点附近会显示出明显的区别。考虑到整体状态方程密度范围非常大，两种近似方法得到的自由能等性质差别可以忽略，并不影响状态方程的整体行为。

1 Burrows A, Livne E, Dessart L, et al. A new mechanism for core-collapse supernova explosions[J]. The Astrophysical Journal, 2006, 640: 878-890

2 Janka H Th, Langanke K, Marek A, et al. Theory of core-collapse supernovae[J]. Physics Reports, 2007, 442: 38-74

3 Sumiyoshi K, Yamada S, Suzuki H, et al. Postbounce evolution of core-collapse supernovae: long-term effects of the equation of state[J]. The Astrophysical Journal, 2005, 629: 922-932

4 Shen H, Toki H, Oyamatsu K, et al. Relativistic equation of state for core-collapse supernova simulations[J]. The Astrophysical Journal Supplement Series, 2011, 197: 20-33

5 Lattimer J M, Swesty F D. A generalized equation of state for hot, dense matter[J]. Nuclear Physics A, 1991, 535: 331-376

6 Shen H, Toki H, Oyamatsu K, et al. Relativistic equation of state of nuclear matter for supernova explosion[J]. Progress of Theoretical Physics, 1998, 100: 1013-1031

7 Shen H, Toki H, Oyamatsu K, et al. Relativistic equation of state of nuclear matter for supernova and neutron star[J]. Nuclear Physics A, 1998, 637: 435-450

8 Shen G, Horowitz C J, Teige S. New equation of state for astrophysical simulations[J]. Physical Review C, 2011, 83: 035802

9 Centelles M, Schuck P, Viñas X. Thomas-Fermi theory for atomic nuclei revisited[J]. Annals of Physics, 2007, 322: 363-396

10 Avancini S S, Brito L, Marinelli J R, et al. The pasta phase within density dependent hadronic models[J]. Physical Review C, 2009, 79: 035804

11 Avancini S S, Chiacchiera S, Menezes D P, et al. Warm“pasta” phase in the Thomas-Fermi approximation[J]. Physical Review C, 2010, 82: 055807

12 Sugahara Y, Toki H. Relativistic mean-field theory for unstable nuclei with non-linear σ and ω terms[J]. Nuclear Physics A, 1994, 579: 557-572

13 Oyamatsu K. Nuclear shapes in the inner crust of a neutron star[J]. Nuclear Physics A, 1993, 561: 431-452

CLCTL99

Relativistic equation of state for non-uniform nuclear matter

ZHANG Zhaowen SHEN Hong
(School of Physics, Nankai University, Tianjin 300071, China)

Background: The self-consistent Thomas-Fermi approximation has been widely used in atomic and nuclear physics. Many properties of nuclei can be described by the Thomas-Fermi approximation in good agreement with experimental data. Purpose: We studied the non-uniform nuclear matter using the self-consistent Thomas-Fermi approximation with a relativistic mean-field model. Methods: The non-uniform matter was assumed to be composed of a lattice of heavy nuclei surrounded by dripped nucleons. We determined the thermodynamically favored state by minimizing the free energy density with respect to the radius of the Wigner-Seitz cell, while the nucleon distribution in the cell was determined self-consistently in the Thomas-Fermi approximation. Results: A detailed comparison is made between the present results and previous calculations in the Thomas-Fermi approximation with a parameterized nucleon distribution that has been adopted in the widely-used-Shen-EOS (equation of state). Conclusion: It has been found that there is no obvious difference in nucleon distributions at lower densities, while the difference becomes noticeable near the transition density to uniform matter. For thermodynamical quantities, such as the free energy and entropy per baryon, the results of both methods generally agree well with each other.

Non-uniform nuclear matter, Equation of state

TL99

10.11889/j.0253-3219.2014.hjs.37.100514

国家自然科学基金(No.11075082、No.11375089)资助

张肇文，男，1987年出生，2010年毕业于南开大学，理论物理专业

申虹，E-mail: songtc@nankai.edu.cn

2014-04-21，

2014-09-01