基于Matlab工具箱的摄像机标定

王建强， 张海花

(浙江师范大学工学院，浙江金华321004)

0 引言

一套典型的双目视觉测量系统由2台CCD摄像机、1台计算机组成。作为一套经典的光机电算一体化系统，CCD摄像机的标定结果对保障系统测量精度起着决定性的作用。一般情况下，标定测量系统需要引入高精度的电动平移台等精密设备来标定系统，同时也引入很多不必要的误差［1-4］。目前普遍采用的摄像机模型是针孔加畸变模型［5-7］。根据参数的性质不同，摄像机的基本参数可分为内参数和外参数，内参数指主点位置、焦距、畸变系数、倾斜因子等摄像机本身具有的参数;外参数是指摄像机在世界坐标系中的位置和方向。利用摄像机模型求解内、外部参数的过程被称为摄像机标定。

1 摄像机模型

如图1所示，理想情况下摄像机的成像模型［8-13］可以用针孔模型表示，其中，XwYwZw为世界坐标系;XcYcZc为摄像机坐标系。p点世界坐标(Xw，Yw，Zw)与其摄像机坐标(Xc，Yc，Zc)之间的关系可表示为

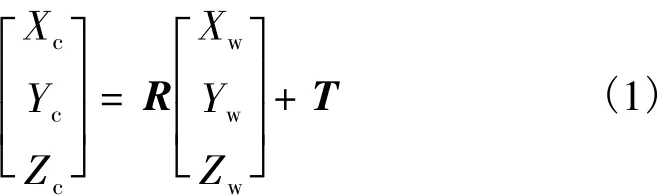
式中:R为世界坐标系到摄像机坐标系的旋转矩阵;T为平移向量。

由于摄像机存在光学系统的加工误差和装配误差，实际的成像系统与理想的针孔模型之间存在光学畸变误差。镜头畸变主要有径向畸变和切向畸变。令x=Xc/Zc，y=Yc/Zc，对摄像机坐标归一化，则径向畸变 δxrδyr可表示为

图1 摄像机模型

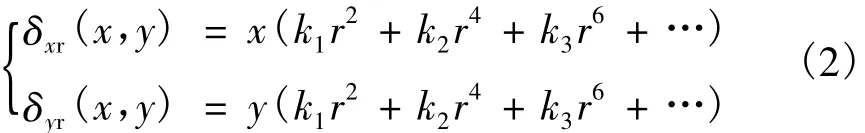
式中:r2=x2+y2;k1，k2，…为摄像机的径向畸变参量。

切向畸变 δxtδyt可表示为

式中，p1、p2为摄像机的切向畸变参量。

在考虑摄像机畸变之后，p点在归一化摄像机坐标系中的实际坐标(xd，yd)可表示为

再由透视变换可以得到p点在图像坐标系中的坐标(u，v):

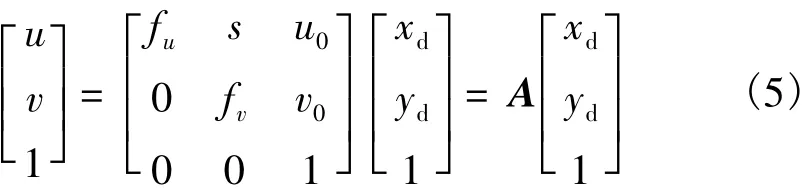
式中:fu、fv分别为u、v 2个方向的归一化焦距;s为坐标轴的倾斜因子;u0、v0分别为主点的图像坐标;

式(1)中的旋转矩阵R、平移矢量T即为摄像机的外部参数，表示了摄像机在世界坐标系里的位置和方向。由式(2)～(5)可以得到CCD摄像机的内参数有 fu、fv、s、u0、v0。考虑镜头畸变之后，内参数还有 k1、k2和 p1、p2。

2 实验过程及结果

如图2所示，张正友等提出了基于2D平面靶标的摄像机标定方法［14-15］，实验中采用了棋盘格作为2D平面靶标，选取了棋盘格的顶点作为特征点标定摄像机各项参数。假设摄像机内部参数均为常数，将2D平面靶标在测量体积内摆放若干位置。在测量体积内，2D的平面靶标可以自由移动，无需知道运动的参数。CCD摄像机拍摄了28组不同位置和角度的平面靶标图像。考虑旋转矩阵的单位正交性，得出摄像机参数。在标定过程中，假设摄像机内部参数始终不变，即不论摄像机从哪个角度拍摄靶标，摄像机内部参数都是常数，只有外部参数发生变化。在此双目视觉测量系统中，左右2个摄像机的内外参数分别为:

图2 二维平面靶标

(1)左侧摄像机内部参数。焦距fcl=［594.22，591.74］;主点 ccl= ［154.33，254.46］;径向畸变k1l= －0.14，k2l=0.26; 切向畸变p1l= －3.1 ×10－3，p2l= －8.7 ×10－4。

(2)右侧摄像机内部参数。焦距 fcr=［3 675.41，3 670.17］;主点 ccr= ［806.61，612.92］;径向畸变k1r= －0.17;k2r=0.88; 切向畸变 p1r=1.72 ×10－3;p2r=1.13 ×10－3。

如图3所示，标定摄像机之后，根据求出的摄像机参数，重构了摄像机与不同位置靶标之间的位置关系。

图3 摄像机与靶标位置关系

采用Matlab立体标定工具箱对此双目视觉测量系统中的2个CCD摄像机的内部、外部参数进行处理。根据摄像机坐标系和世界坐标系之间的关系，进行立体标定，得到2个CCD摄像机坐标系之间的位置关系:旋转矢量R，平移矢量T。图4表示了左右2个CCD摄像机与靶标特征点之间的位置关系。图中所示的双目视觉测量系统立体标定结果如下:

左右摄像机相对旋转矢量R=［－2.9×10－2，0.38，－1.17 ×10－3］;相对平移矢量 T= ［－200.34，100.35，150.75］。

我们在标定后的双目视觉测量系统的测量体积内放置一个标准的台阶模型进行测量，该模型的左侧由多个平行平面组成，相邻平面之间的间距均为1.00 mm，右侧为一标准斜面。图5为该台阶模型的三维重构结果，采用最小二乘法依次拟合平面方程，计算可得相邻平行平面之间的距离为0.99 mm。

图4 系统立体标定结果

图5 台阶模型测量结果

3 结语

摄像机的标定是双目视觉测量系统的关键技术之一，一般情况下需要引入高精度平移台等设备来标定。采用3D立体靶标是比较传统的方法，通过在空间构造一系列相对位置已知的标记点来估计参数。但是3D立体靶标的制作成本较高，且精度受到一定限制。本文借助于2D平面靶标，降低了标定靶标的制作难度;采用张正友的方法，利用Matlab工具箱标定CCD摄像机的内、外部参数，通过立体标定得出两台CCD摄像机之间的位置关系。最后对一个标准的台阶模型进行测量，并恢复其三维形貌。

［1］ Wu F C，Hu Z Y，Zhu H J.Camera calibration with moving onedimensional objects［J］.Pattern Recognition，2005，38:755-765.

［2］ Limei Song，Mingping Wang，Lu Lu，et al.High precision camera calibration in vision measurement［J］.Optics ＆ Laser Technology，2007，39:1413-1420.

［3］ Armstrong M，Zisserman A，Hartley R.Self-calibration from Image Triplets［C］∥Proc of European Conference on Computer Vision.UK:Cambridge，1996:3-16.

［4］ Pollefeys M，Koch R，Van Gool L.Self-calibration and Metric Reconstruction in Spite of Varying and Unknown Internal Camera Parameters［C］∥ Proc of International Conference on Computer Vision.India:Bombay，1998:90-95.

［5］ 张 伟，程 鸿，等.摄像机标定系统的设计与实现［J］.计算机工程，2007(2):681-683.

［6］ Guo-Qing W E I，Song De M A.A complete two-plane camera calibration method and experimental comparisons［C］∥IEEE Proc 4th International Conference on Computer Vision，Berlin，Germany，1993:439-446.

［7］ 张海花，李 勇，许富洋.结构光三维成像系统的计算机仿真［J］.光学与光电技术，2009，7(3):64-66.

［8］ Wu Fuchao，Li Hua，Hu Zhanyi.A new camera self-calibration method based on active vision system［J］.Chinese Journal of Computers，2000，23(11):1130-1139.

［9］ Fei Qi，Qihe Li，Yupin Luo，et al.Camera calibration with onedimensional objects moving under gravity［J］.Pattern Recognition，2007，40:343-345.

［10］ Yang C J， Hu Z Y. An intrinsic parameters self-calibration technique for active vision system［C］∥Proc of International Conference on Pattern Recognition.Brisbane，1998:67-69.

［11］ 张广军.视觉测量［M］.北京:科学出版社，2008:14-32.

［12］ 马颂德，张正友.计算机视觉—计算理论与算法基础［M］.北京:科学出版社，1998.52-71.

［13］ Janne Heikkil， Olli Silvén. A four-step camera calibration procedure with implicit image correction［C］∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition，San Juan，1997:1106-1112.

［14］ 张海花，李 勇，张海燕.采用虚拟标准平面标定相位测量轮廓术系统［J］.激光技术，2010，34(5):600-602.

［15］ Zheng-you ZHANG.A flexible new technique for camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11):1330-1334.